Введение
Реальные условия функционирования сложных систем характеризуются воздействием внешней среды, а процесс управления проходит в условиях помех. Возможность возникновения в сложных системах кризисных явлений влечет за собой необходимость применения методов антикризисного подхода [5]. Антикризисное управление (АКУ) рассматривается как процесс предотвращения или преодоления кризиса объекта управления (ОУ) [1]. В предыдущих работах [2,4,5,6,8] авторами рассматривались вопросы поддержки принятия решений на основе антикризисного подхода для различных классов сложных систем (организационно-технических систем, экономических объектов). Кроме того, авторами исследовались вопросы интеграции интеллектуальных технологий в этих задачах [5–7]. Данная статья посвящена вопросам применения антикризисного подхода для управления многозвенным манипулятором, который относится к классу сложных технических объектов.
Причиной кризиса сложного технического объекта может быть не только износ [5], но и особенности эксплуатации – например, удар о препятствие, в результате которого произошло повреждение манипулятора, груза или препятствия. Поиск траекторий безударного движения манипулятора является важной составляющей сложной задачи управления многозвенным манипулятором. В статье рассматривается математическое и программное обеспечения для поддержки антикризисных решений для многозвенного манипулятора как сложного технического объекта.
Цели и задачи антикризисного управления сложным техническим объектом
Среди основных задач АКУ для выделенного класса сложных технических объектов (многозвенного манипулятора) можно отметить: учет возможных прогнозов и разработка эффективных антикризисных сценариев; мониторинг кризисных ситуаций; обеспечение оперативности и гибкости антикризисного управления при изменении ситуации [1,5]. При этом АКУ имеет ряд особенностей: выбор наилучшего антикризисного сценария – необходимо найти наилучшую безударную траекторию; существенная зависимость от фактора времени – необходимо определить безударную траекторию в режиме реального времени; специфические критерии при выборе вариантов решения (минимизация потерь, учет факторов риска, предотвращение тяжелых последствий и др.) – безударная траектория должна соответствовать поставленным ограничениям (по длине манипулятора, углам поворота и др.); необходимость в предварительной проработке вариантов управленческих решений и оценке их последствий – безударные траектории необходимо определить до начала движения манипулятора и оценить их с точки зрения выбранных критериев; необходимость компьютерной поддержки разработки сценариев – расчет безударных траекторий должен происходить с помощью информационных технологий; необходимость учета предыдущего опыта. Математическое и программное обеспечения должно содержать методы и алгоритмы нахождения антикризисных сценариев (безударных траекторий, обеспечивающих сохранность манипулятора, груза и препятствий рабочего пространства).
Математическое обеспечение для поиска безударных траекторий
Трудности разработки алгоритмов поиска безударных траекторий связаны с большим количеством звеньев манипулятора, а также сложностью рабочего пространства. Траектория манипулятора однозначно описывается набором точек в пространстве (узловыми точками). Траектория не должна пересекать препятствия, расположенные в рабочем пространстве. Требуется разработать алгоритм для поиска траектории движения манипулятора в сложном пространстве по критерию минимальной длины траектории. Заданы: координаты основания (x1, y1); координаты цели (xq, yq); W – максимальное количество звеньев; αmax – максимально допустимый угол поворота звена. Зададим целевую функцию G=f(Z), где Z={(x1, y1),(x2, y2),…, xk,yk)} – множество узловых точек траектории, причем Z однозначно определяет траекторию Т манипулятора. Необходимо найти Z такое, что G(Z) → min (G) при ограничениях, задаваемых системой уравнений:
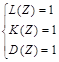
при этом функции L = f1(n, Z), K = f2(n, Z), D = f3(n, Z) определены как:
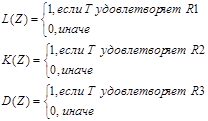
Условия R1, R2, R3 определены в таблице 1.
Таблица 1. Значения условий
|
№ |
Значение |
|
R1 |
Пригодность траектории по не пересечению участков траектории друг с другом и с препятствиями. Задается системами уравнений и неравенств. Для траектории из r участков и пространства из m отрезков: |
|
R2 |
Пригодность траектории с точки зрения кинематики манипулятора: n=s/l, где n – число звеньев, s – длина траектории, l – длина звена , 0<n≤W, n – целое число; ni=si/l, где si – длина i-того участка траектории, ni – целое число; - αmax≤ αi ≤ αmax, где αi – угол поворота (i+1)-го участка траектории относительно i-го участка, i=1, n-1. |
|
R3 |
Пригодность траектории по точности достижения цели: d ≤ h, где d – расстояние от последней точки траектории до цели, h – заданная точность. |
Данная задача принадлежит к классу задач нелинейного программирования с большим числом ограничений и имеет возрастающую сложность, поэтому решение задачи стандартными методами занимает много времени. Известные методы поиска траекторий многозвенных манипуляторов (метод псевдоинверсии, метод обратных преобразований, метод потенциального поля и др.) дают приемлемые результаты для относительно небольшого числа препятствий и звеньев [3]. Для большего числа звеньев сложность вычислений возрастает, время нахождения решений резко увеличивается, а в случае сложного рабочего пространства эти методы требуют дополнительной доработки. Для поддержки антикризисного управления СТО на этапе эксплуатации при решении задачи поиска безударных траекторий предлагается подход, основанный на применении генетического алгоритма.
Генетический алгоритм для поиска безударных траекторий
В терминах генетического алгоритма (ГА) [9] задачу поиска безударных траекторий можно сформулировать следующим образом – необходимо найти траекторию, которая будет удовлетворять следующим критериям: пригодность по достижению цели; пригодность по допустимости углов поворота; пригодность по пересечению с препятствиями; пригодность по достаточности длины манипулятора; пригодность по укладываемости и достаточности звеньев манипулятора; пригодность по толщине манипулятора. При этом траектория должна быть найдена за определенное, конечное число шагов.
В качестве гена выступает узловая точка траектории. Траектория интерпретируется как хромосома. Начальная популяция генерируется с помощью датчика псевдослучайных чисел построением траекторий, непересекающихся с препятствиями. Работа с популяцией ведется с помощью генетических операторов скрещивания, мутации, селекции, отбора элиты. Эти вопросы освещены в [3]. Перед началом работы генетического алгоритма происходит инициализация популяции. Далее состав популяции динамически изменяется на каждом шаге-итерации. Эти изменения моделируются генетическими операторами, которые применяются до тех пор, пока не будет получена конечная популяция, заданная с помощью критериев оценки, например, в конечной популяции должно быть n пригодных траекторий или не истечет заданное число шагов. В результате из набора пригодных траекторий выбирается наилучшая по критерию минимальной длины.
Определение пригодности траекторий осуществляется по следующим параметрам:
1. Пригодность по достижению цели: определяется вычислением расстояния между целевой точкой ![]() , задаваемой оператором, и конечной точкой траектории
, задаваемой оператором, и конечной точкой траектории ![]() по формуле:
по формуле: ![]() (1).
(1).
Если это расстояние удовлетворяет требованиям погрешности достижения цели, устанавливается признак пригодности траектории по данному параметру.
2. Пригодность по достаточности длины манипулятора: определяется вычислением длины траектории по формуле (1) путем сложения длин всех звеньев.
3. Пригодность по укладываемости и достаточности звеньев манипулятора: данная операция представляет собой проверку на укладываемость звеньев манипулятора в звенья траектории и проверку на достаточность количества звеньев для прохождения по данной траектории. Для вычисления длин звеньев траектории и манипулятора используется формула (1).
4. Пригодность по допустимости углов поворота: осуществляется путем вычисления угла поворота между всеми звеньями траектории и сравнения их с нормативными значениями. Угол поворота звеньев относительно друг друга вычисляется по формуле:
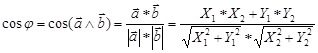 (2),
(2),
где ![]() и
и ![]() – направляющие вектора соседних звеньев траектории;
– направляющие вектора соседних звеньев траектории;
![]() – координаты этих векторов.
– координаты этих векторов.
5. Пригодность по пересечению с препятствиями: осуществляется как проверка всех пар звеньев траектории и отрезков препятствий на наличие точки пересечения (вычисляются уравнения прямых y=kx+b для звена траектории и отрезка препятствия, после чего определяется точка пересечения (если существует).
6. Пригодность по толщине манипулятора: рассматриваются все пары отрезков препятствий и звеньев траекторий, определяется их взаимное расположение в рабочем пространстве и вычисляется расстояние между ними для сравнения с нормативным. Для этого:
1) Вычисляется уравнение прямой звена траектории вида: y=kx+b (3).
2) Уравнение вида (3) приводится к общему виду: Ax+By+C=0 (4).
3) Вычисляется нормирующий множитель по формуле: ![]() (5).
(5).
4) Уравнение вида (4) нормируется умножением на нормирующий множитель μ вида (5). Получаем нормальное уравнение прямой вида: ![]() (6).
(6).
5) Расстояние между прямой звена и любой точкой препятствия вычисляется по формуле: ![]() (7), где X, Y – координаты точки отрезка препятствия.
(7), где X, Y – координаты точки отрезка препятствия.
6) Вычисляются координаты основания перпендикуляра, опущенного из точки препятствия, и если расстояние d меньше толщины звена и основание перпендикуляра попадает на звено траектории, она считается непроходимой.
Программная реализация алгоритмов поиска безударных траекторий
Для повышения эффективности работы базового алгоритма предлагается интеграция технологий генетического алгоритма и экспертных систем с учетом идеологии АКУ. Модуль 1 экспертной системы предназначен для формирования рекомендаций по генерированию начальной популяции и применяется для обеспечения целенаправленности траекторий начальной популяции. Модуль 2 экспертной системы предназначен для формирования рекомендаций по скрещиванию траекторий и обеспечивает более высокую вероятность скрещивания для траекторий, удовлетворяющих условиям пригодности (рис. 1). Более подробно этот вопрос рассмотрен в [3].
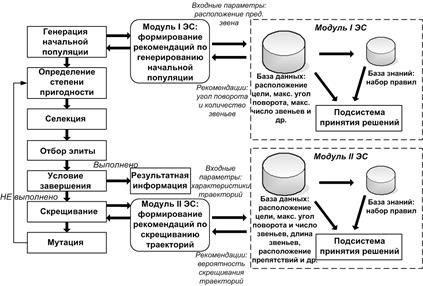
Рис. 1. Интеграция генетического алгоритма и технологии экспертных систем в задаче поиска антикризисных сценариев при поиске безударных траекторий СТО
В разработанном прототипе СППР для поиска безударных траекторий многозвенного манипулятора (рис. 2) автоматизированы следующие функции: моделирование рабочего пространства; моделирование параметров СТО; моделирование процесса поиска траекторий с учетом заданных параметров СТО и рабочего пространства. СППР начинает работу с моделирования рабочего пространства, параметров СТО и параметров генетического алгоритма. По окончанию этого этапа СППР переходит на этап поиска траекторий движения манипулятора, после чего осуществляется обработка полученных данных и их представление лицу, принимающему решения (ЛПР). Разработанное программное обеспечение было протестировано на различных видах рабочего пространства (лабиринт, тоннель, рабочее пространство с большим количеством одинаковых по форме препятствий, рабочее пространство с большим количеством различных по форме препятствий) и позволило провести компьютерные эксперименты. Для проверки работоспособности и оценки эффективности рассмотренных методов была проведена серия экспериментов. В ходе экспериментов варьировались величина угла между звеньями, количество звеньев, а также производились замеры достижимости цели и среднего времени ее поиска.
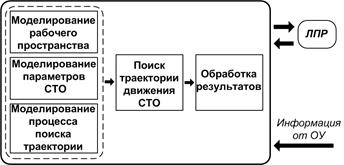
Рис. 2. Прототип СППР для ОУ СТО
Анализ экспериментальных данных показал высокую эффективность поиска безударных траекторий для обеспечения безопасности функционирования самого ОУ и препятствий, его окружающих. Установлено, что для разработанных методов поиска безударных траекторий средний процент достижения точек составляет 70–85 % при достаточно большом числе звеньев (до 60). Предложенные методы и алгоритмы поиска траекторий движения ОУ на примере многозвенного манипулятора можно использовать для различных типов рабочего пространства с препятствиями.
Заключение
В статье рассмотрены вопросы разработки математического и программного обеспечения для задачи поиска траекторий многозвенного манипулятора, которая рассматривается как составляющая задачи управления сложным техническим объектом на основе антикризисного подхода. В качестве кризисной ситуации в данном случае рассматривается возможность нарушения функционирования вследствие столкновения манипулятора с препятствиями в процессе движения к цели. Применение антикризисного подхода дает возможность предупредить такие ситуации и обеспечить сохранность манипулятора и препятствий, так как основными решаемыми задачами в соответствии с методологией АКУ [5] в данном случае являются учет возможных прогнозов и разработка эффективных антикризисных сценариев в виде безударных траекторий многозвенного манипулятора. Для решения этой задачи рассматривается базовый генетический алгоритм и его дальнейшая интеграция с технологией экспертных систем. Разработанные методы поиска траекторий обеспечивают качественно новые возможности при решении задач АКУ СТО: учет возможностей кризисов (предотвращение столкновений), разработку эффективных антикризисных сценариев (нахождение безударных траекторий по критерию минимальной длины) и получение качественно новых решений, а именно – увеличение вероятности нахождения наилучшей траектории по критерию минимальной длины, уменьшение времени поиска решения, улучшение «проходимости» в узких тоннелях, адаптация базового генетического алгоритма к различным видам рабочего пространства.
Рецензенты:
Мунасыпов Р.А., д.т.н., профессор, профессор кафедры технической кибернетики ФГБОУ ВПО УГАТУ, г.Уфа.
Картак В.М., д.ф.-м.н., доцент, заведующий кафедрой прикладной информатики ФГБОУ ВПО БГПУ, Уфа.



