Введение
По большинству технических факторов и, прежде всего по интенсивности сигнала, его частоте, времени действия импульса, направленности, времени прихода, знака вступления (полярности), помехоустойчивости, проникающей и разрешающей способностям, избирательности, сейсморазведка намного превосходит все другие геофизические методы. Вместе с тем сейсмическим методам присущи ограничения, накладываемые проникающей возможностью и разрешающей способностью. В наиболее общей форме разрешающая способность сейсмометрии есть способность сейсмических методов с максимальной детальностью выделять и описывать трехмерные тела произвольной конфигурации со специфическими упругими свойствами, расположенные случайным образом относительно источника и приемника [Кунин, Шейх-Заде, 1].
В сейсморазведке разрешение – процесс разделения составляющих отражений, при этом составляющие отражение – переменные, которые включают: 1)переменную времени, определяемая как размерность требуемого времени отражения, например, доминирующий период; 2) переменную формы волны, как безразмерная переменная независимая от линейного времени и амплитудной калибровки отражения, например, отношения амплитуд главного и смежного лепестков стороны отражения.
Весьма очевидно, какую роль в разрешении сейсмического сигнала играет переменная времени. но возникает вопрос, какова роль переменной формы волны разделения. Когда несколько составляющих отражений находятся близко друг к другу, разрешение этих отражений не может быть выражено с точки зрения одной только переменной времени, форма волны отражений также должна быть принята во внимание. Теоретически каждое сейсмическое отражение есть дельта функция (единичный импульс), амплитуда которого равна значению коэффициента отражения. Именно группа таких единичных отражений и описывает нашу геологическую модель. На практике мы имеем сейсмическую трассу, которая является результатом свертки трассы единичных отражений и сейсмического импульса сигнала, кроме того, она также является результатом суперпозиции кратных отражений, волн помех и дополнительных шумов, которые сильно изменяют (искажают) форму видимого сигнала. Именно поэтому, говоря о степени разрешенности сейсмического сигнала, мы должны иметь в виду не только длительность сигнала, но и его форму (рис. 1).
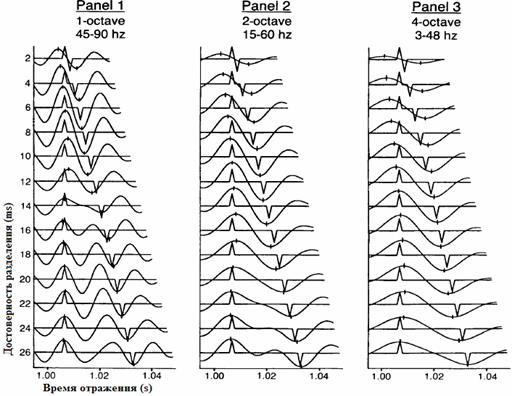
Рис. 1 Сравнение коэффициентов отражения для трех вариантов волн сигнала [Widess, 6]
Следовательно, в отсутствие шума у отражения есть две фундаментальные переменные, описывающие его разрешение: переменная времени и переменная формы волны. Переменная времени будет связана с шириной главного периода сигнала. Меньшая ширина для данной формы волны способствует разрешению, потому что отражение близко к единичному импульсу. Переменная формы волны связана с процентом отражательной энергии, которая находится в самом сигнале. В дополнение к переменной времени и переменной формы волны можно выделить третью фундаментальную переменную, имеющую отношение к степени разрешения – шум.
На основе данных умозаключений в 1982 году, а затем и в 1989 году M. B. Widess предложил общую формулу (1) для расчета коэффициента разрешенности PR (power resolving) сейсмической записи для известной формы отраженного сигнала:
(1)
где 
-- максимальная (абсолютная) амплитуда сигнала, E – энергия волны, q – сигнал, который определяется по формуле:
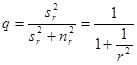(2)
где 
и 
-- среднеквадратичные значения сигнала и помехи на сейсмической трассе соответственно; 
– энергетическое соотношение сигнал/помеха.
Поскольку в реальных случаях точная форма отраженного сигнала неизвестна, то используются приближенные оценки. На основе автокорреляционной функции трассы Гогоненков [2] предложил оценку разрешенности, не учитывающей истинный фазовый спектр сигнала:
(3)
где 
– ширина главного полупериода автокорреляционной функции (АКФ); S1 – площадь главного полупериода; S2-4 – суммарная площадь последующих трех полупериодов.
На практике мы работаем с дискретными функциями, а значит, формулу 3 можно записать в виде:
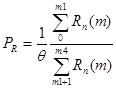(4)
где m1 -- интервал отсчетов равный ½ T (); m4 -- интервал отсчетов равный 2T (T – видимый период); Rn – нормированное значение АКФ (Rn=R(m)/R0).
Очевидно, что если 
→0, то запись имеет хорошее разрешение, так как вся энергия сигнала будет сосредоточена в первом полупериоде. В противном случае если 
→ 
, то запись плохо разрешена, т.е. можно считать, что многофазное исходное колебание связано с положением нескольких волн.
Часто на практике нас интересует разрешенность записи в малом интервале, поэтому вопросы точности определения АКФ приобретают большое практическое значение. Определить погрешность оценки [Никитин, 3] АКФ можно как:
(5)
где n – количество дискретов функции.
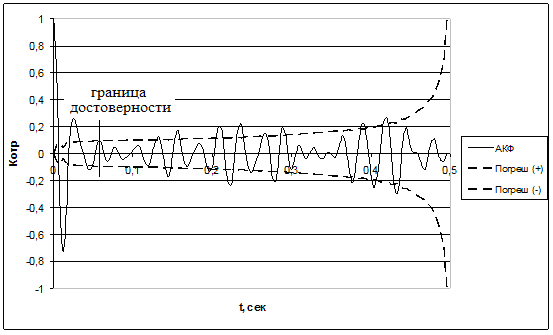
Рис. 2 Функция автокорреляции и график оценки погрешности для модельной трассы с несущей частотой 32 Гц.
Погрешность оценки АКФ возрастает с увеличением длины самой функции. При Rn < 
значения АКФ не являются доверительными. Согласно рис. 2 граница достоверности равна четырем полупериодам АКФ, а значит, коэффициент разрешенности можно рассчитать по формуле 4.
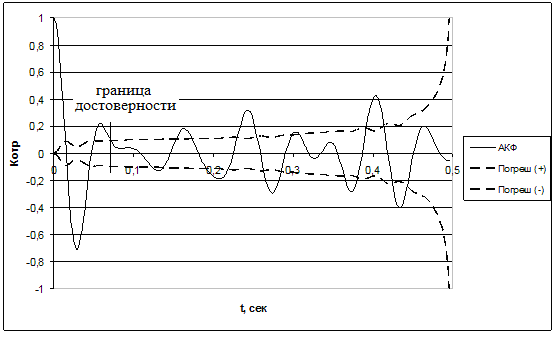
Рис. 3 Функция автокорреляции и график оценки погрешности для модельной трассы с несущей частотой 16 Гц.
С понижением частоты сигнала, что зачастую наблюдается на практике, происходит «растягивание» энергии сигнала. При этом определение коэффициента разрешенности по формуле 4 неверно, а именно влечет за собой ошибку при вычислении. Расчет коэффициента погрешности стоит производить на интервале АКФ, не превышающим границу достоверности, что показано на рис.3. Формула 4 с учетом данного утверждения принимает вид:
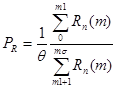(6)
где mσ – интервал отсчетов равный граничному времени, удовлетворяющему условию достоверности.
Формулу 6 очень сложно применять для автоматического расчета коэффициента разрешенности, ввиду того, что график погрешности должен строиться для каждой сейсмической трассы, именно поэтому на основе лабораторных моделей и реальных сейсмических данных предлагается эмпирическая формула 7, в которой интервал mσ для расчета энергии выбирается равным 3:
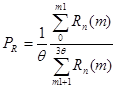(7)
где m1 -- интервал отсчетов равный ½ T (); Rn – нормированное значение АКФ (Rn=R(m)/R0).
Процедура расчета коэффициента разрешенности применяется для единичной трассы, то есть является независимой от других трасс в наборе и рассчитывается индивидуально. Для анализа не только единичных сейсмических трасс, а также и групп трасс, предлагается рассчитывать на основе формулы 7 арифметическое среднее или медианное значения, рассчитанные по всем трассам. Отсюда следует, что с увеличением количества трасс при расчете общего значения разрешения, увеличивается точность расчета, при этом ограничение расчета зависит от технических характеристик устройств расчета (память и тактовая частота). Кроме того, коэффициент разрешенности можно использовать в комплексе с сейсмическим разрезом. Комплексный анализ позволяет определять области с повышенными и пониженными значениями, которые в дальнейшем позволяют сделать количественный анализ сейсмической информации, а именно степени их разрешенности. Данный подход можно применять не только для комплексного и количественного анализа сейсмических данных, но и для эффективного контроля применения процедур деконволюции и миграции при обработке сейсмического сигнала. Более подробно применение коэффициента разрешенности рассмотрено в работах [4],[5]. Пример использования коэффициента разрешенности для контроля коррекции статических и кинематических поправок приведен на рис 4. Наглядно видно, что некоторые зоны с малыми значениями коэффициента разрешенности сильно меняются после очередной коррекции. Они становятся более разрешенными, при этом цвет меняется с синего на красный, т.е. коэффициент разрешенности растет, а значит улучшается сейсмическая разрешенность записи. Как видно из рис.4 существуют зоны с ярко выраженными осями синфазности, но с низкими значениями коэффициента разрешенности. Это объясняется тем, что в этом интервале преобладают низкие частоты, которые не позволяют сильно разрешить волновую картину.
Подход, основанный на примере использования коэффициента разрешенности, универсален для оценки сейсмических данных на любом из этапов обработки сигнала, кроме того, он независим и эффективен при использовании, позволяет оценить качество данных быстро и надежно и получить оптимальный результат при обработке и интерпретации.
Рис.4 Применение коэффициента разрешенности для контроля работы процедур коррекции статических и кинематических поправок
Рецензенты:
Нежданов А.А., д.г.-м.н., профессор ТюмГНГУ, заместитель начальника по научной работе ИТЦ ООО «Газпром геологоразведка», г.Тюмень.
Кузнецов В.И., д.г.-м.н., профессор ТюмГНГУ, заместитель генерального директора ООО «Новатэк НТЦ»., г.Тюмень.