Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Введение

С точки зрения современной теории и практики автоматизации управления недостаточно проработанными остаются вопросы эффективного управления оборудованием, учитывающего необходимость адаптации параметров их функционирования. Для повышения качества работ по разработке и эксплуатации АСУ сложных систем технологического оборудования целесообразным является применение вероятностного имитационного моделирования. Статистические распределения случайных величин параметров функционирования технологического оборудования, полученные на базе теоретических и экспериментальных исследований, позволяют повысить точность и эффективность моделирования сложных стохастических систем.

Статистические исследования сложных систем технологического оборудования требуют проведения большого объёма исследований по получению, накоплению, обработке и анализу информации, важнейшим этапом которых являются хронометражные наблюдения за работой отдельных машин с применением технических средств и инструментальных методов измерения.

Материалы и методика исследования

Сбор хронометражных данных начинается с эскизирования схемы работы объекта наблюдения, занесения в журнал его технико-технологических параметров. В начале и конце каждой смены фиксируются затраты времени на подготовительно-заключительные операции. Затраты времени на основные и вспомогательные операции фиксируются от момента окончания i-ой операции до момента окончания (i + 1)-ой операции. Для получения информации о надежности оборудования используются журналы наблюдений и регистрации отказов, ведущиеся диспетчерской службой и службой главного механика обследуемого предприятия.

После сбора первичной информации выполняется ее статистическая обработка и анализ. Статистическая обработка хронометражных данных заключается в подборе некоторого известного распределения (теоретического), моделирующего с определённой степенью точности эмпирическое статистическое распределение случайной величины X, согласно алгоритму, реализованному на ЭВМ (рис. 1).

Проверка правдоподобия гипотез о виде закона распределения (согласованность теоретического и статистических распределений) основана на определении расхождений между теоретическими вероятностями Pi и наблюдаемыми частотами Pi*. При этом за меру расхождения принят критерий согласия Пирсона (критерий c2) [2]:

,

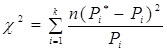где k – число интервалов распределения; Рi – вероятности попадания случайной величины в i-ый интервал с границами xi и xi+1); n – число опытов (наблюдений).

При использовании критерия c 2 достаточно велико должно быть не только общее количество опытов n, но и число наблюдений пi в отдельных интервалах. Рекомендуется иметь в каждом интервале не менее 5–10 наблюдений. Если число наблюдений в отдельных интервалах менее 5, имеет смысл объединить интервалы.

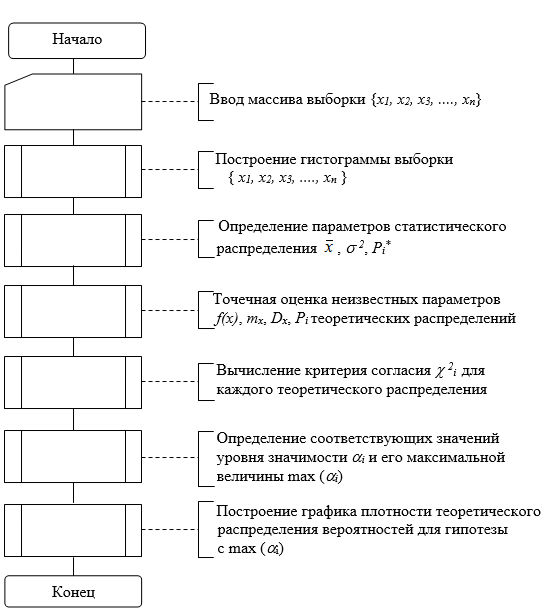
Рис. 1. Блок-схема алгоритма статистической обработки хронометражных данных

Результаты исследования и их обсуждение

В соответствии с изложенной методикой статистических исследований были проведены хронометражные наблюдения за работой базового оборудования стеклотарного производства. Для получения данных о надежности оборудования использовались журналы наблюдений и регистрации отказов, ведущиеся диспетчерской службой и службой главного технолога. Некоторые результаты статистической обработки хронометражных данных приведены в таблице 1.

Таблица 1. Результаты статистической обработки хронометражных данных

, , – математическое ожидание соответственно оперативного времени, наработки на отказ и восстановления; , , – дисперсия соответственно оперативного, наработки на отказ и восстановления; времени; , , – уровень значимости распределения соответствующей случайной величины; , , – функция плотности вероятностей соответствующей случайной величины.

Анализ табличных данных показывает, что статистические распределения случайных величин технико-технологических параметров функционирования оборудования достаточно хорошо апроксимируются тремя теоретическими законами: нормальным, экспоненциальным и логнормальным. Нормальному закону распределения подчиняются случайные значения времени выполнения основных и вспомогательных операций, выполняемых технологическим оборудованием линии по производству стеклотары, а также величины загрузки шихты и стеклобоя в стекловаренную печь при уровне значимости, изменяющемуся от 0,09 до 0,99. Экспоненциальному и логнормальному законам распределения подчиняются случайные значения, соответственно, наработки на отказ и времени восстановления всех видов и типов рассматриваемого оборудования при изменении уровня значимости для экспоненциального закона от 0,08 до 0,95 и логнормального – от 0,18 до 0,95. Такой разброс параметра max {αi} вызван субъективными факторами, связанными с ошибками наблюдений в производственных условиях.

На рис. 2 представлены совмещенные графики гистограмм выборки и выравнивающих кривых теоретических распределений для трех законов, полученных при обработке данных наблюдений: нормального, экспоненциального и логнормального. Графики построены применительно к распределениям случайных величин оперативного времени подачи порции шихты и стеклобоя загрузчиком в стекловаренную печь, времени его наработки на отказ и времени восстановления. Выравнивающие кривые описываются функциями вида:

для нормального закона – ;

для экспоненциального закона – ;

для логнормального – .

а)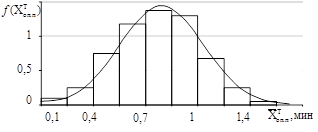 б)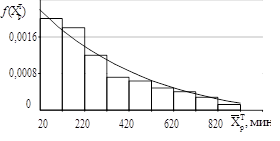

в)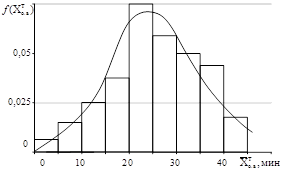

в)

Рис. 2. Гистограммы и кривые теоретических распределений случайных величин функционирования погрузчика смеси шихты и стеклобоя: а) – оперативного времени погрузки порции смеси; б) – наработки на отказ; в) – времени восстановления погрузчика.

Из рис. 2 видно, что теоретические кривые распределения , сохраняя в основном существенные особенности статистических распределений, свободны от случайных неправильностей хода гистограмм, которые могут быть отнесены за счет погрешностей измерения при фотохронометражных наблюдениях. Этот вывод подтверждают высокие уровни значимости max {α} при проверке степени соответствия по критерию Пирсона (c 2) выдвинутых гипотез со статическим материалом: для нормального закона , экспоненциального – , и логнормального –.

Заключение

Полученные теоретические распределения и их числовые характеристики были использованы при синтезе имитационной модели функционирования оборудования линии стеклотарного производства, разработке и реализации ее программного обеспечения [4, 5]. Кроме того, полученные статистические данные можно применять при оценке технической производительности оборудования, использовать эти оценки в процессе формирования альтернативных объекто-вариантов при реализации методики оптимизационных расчетов параметров функционирования машинолинии.

Рецензенты:

Фомин Б.Ф., д.т.н., профессор, профессор кафедры «Автоматики и процессов управления» Санкт-Петербургского государственного электротехнического университета «ЛЭТИ» им. В.И. Ульянова (Ленина), г. Санкт-Петербург.

Коршунов Г.И., д.т.н., профессор, генеральный директор общества с ограниченной ответственностью «Пантес групп», г. Санкт-Петербург.