Введение
Федеральный государственный образовательный стандарт высшего профессионального образования по направлению подготовки 011200-физика определяет, что областью профессиональной деятельности бакалавров являются все виды наблюдающихся в природе физических явлений, процессов и структур [9]. К объектам их профессиональной деятельности относятся физические системы различного масштаба и уровней организации и процессы их функционирования.
Одним из видов профессиональной деятельности бакалавра является научно-исследовательская работа, которая должна быть отражена в образовательной программе, разрабатываемой высшим учебным заведением, осуществляющим подготовку бакалавров физики. В рамках научно-исследовательской деятельности студент должен овладеть методами исследований и уметь применять их при изучении физических систем и их моделей; участвовать в проведении физических исследований и обработке полученных результатов с использованием информационных технологий; научиться работать с научной литературой.
В подготовке студента к решению исследовательских задач важную роль может играть курс теоретической физики, который служит не только для систематизации знаний, полученных при изучении общей физики и математики, выстраивая их архитектуру и углубляя представления о фундаментальных свойствах материи, но, что особенно важно, знакомит студента с методами теоретического исследования объектов природы. В разделах этой дисциплины обосновываются и формируются базовые модели физических систем, сопоставляются результаты теоретических исследований с экспериментальными данными.
Практика преподавания показывает, что студенты часто испытывают затруднения при переходе от решения учебных задач к теоретическому исследованию реальных физических систем. Поэтому возникла необходимость в создании системы задач, ориентированных, с одной, стороны на интеграцию знаний, полученных студентами при изучении различных разделов теоретической физики, а с другой – побуждающих их к исследовательской деятельности.
В данной работе предлагаются учебно-исследовательские задачи, решения которых связаны с формированием моделей макросистем и применением к ним методов статистической физики и термодинамики [6]. Такие задания дают студенту возможность изучать не только качественную картину свойств объектов, но и получать их количественные характеристики. Они могут предлагаться для самостоятельного исследования студентам в качестве проектных заданий. По уровню сложности задачи восходят от самых простых, не требующих владения развитым математическим аппаратом, к сложным теоретическим моделям, которые описываются нелинейными дифференциальными уравнениями и решаются численно с применением компьютерных технологий. При разработке заданий и организации работы студентов использованы методические приемы, направленные на развитие познавательных способностей учащихся, которые описаны в работах [4, 5].
Задачи-оценки для исследования астрономических и планетных систем
Для организации исследовательской деятельности студентов и формирования у них целостных знаний об окружающем мире было разработано учебное пособие [3], где наряду с изложением теоретического материала выстроена система задач-оценок, охватывающих модели материальных объектов разного уровня сложности. Остановимся на примерах задач, в которых рассматриваются объекты астрономического и планетного масштабов [2].
Задача 1. Радиус белого карлика. Белые карлики – звезды, которые при массах, сопоставимых с массой Солнца, имеют очень малые размеры, сравнимые с размерами планет. Вещество этих звезд удерживается от дальнейшего гравитационного сжатия давлением вырожденного электронного газа. Оцените радиус R белого карлика, состоящего преимущественно из гелиевой плазмы, рассматривая звезду в виде однородного самогравитирующего шара с массой M, равной массе Солнца. Электронную компоненту плазмы считать нерелятивистским вырожденным ферми-газом.
Решение. Гравитационная энергия однородного шара массой M и радиусом R выражается формулой 
, где G – гравитационная постоянная. Гравитационные силы стремятся к уменьшению гравитационной энергии, то есть к уменьшению радиуса звезды. Этому противостоит увеличение кинетической энергии частиц.
В звездах рассматриваемого класса кинетической энергией теплового движения ядер можно пренебречь по сравнению с энергией вырожденного электронного газа, равной 
, где N – число всех электронов звезды, а eF – энергия Ферми. В нейтральной гелиевой плазме число электронов равно удвоенному числу ядер гелия, массы которых приблизительно равны учетверенной массе протона mp. Поэтому число электронов находим как 
. Энергия Ферми электронного газа равна
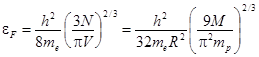. (1)
Суммарная кинетическая энергия электронного газа получается равной
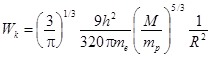. (2)
Отсюда видно, что при изменении радиуса звезды суммарная энергия движения частиц изменяется обратно пропорционально квадрату ее радиуса.
Полная энергия системы при учете основных вкладов равна
, (3)
где введена постоянная, определяемая как
. (4)
Записав условие равновесия системы как условие минимума энергии: 
, приходим к выводу, что параметр R0, представляет собой радиус равновесной звезды.
Полагая массу звезды равной массе Солнца (M = 2×1030 кг), получаем численную оценку радиуса белого карлика: R0 @ 7200 км. Отсюда видно, что карликовая звезда с такой массой, имеющая плотность вещества порядка 10 т/см3, по размерам лишь немногим больше Земли, радиус которой составляет 6370 км.
Задание для исследования. Показать, что при переходе к более реалистичной модели звезды условие равновесия, записанное в виде вариационного уравнения 
, приводит к уравнению радиального распределения относительной массы 
:
, (5)
где x = r/R0 – безразмерная радиальная переменная, h и c – безразмерные постоянные параметры, определяемые массой и составом звезд [8]. Найдите численное решение уравнения (5) для различных значений h и c при граничных условиях: v(0) = 0; v(1) = 1. Рассчитайте радиальные распределения плотности вещества и давления.
Задача 2. Нейтронная звезда. Во Вселенной встречаются объекты еще более плотные, чем белые карлики. Это пульсары или нейтронные звезды, вещество которых представляет собой сверхплотный нейтронный газ, образовавшийся в результате нейтронизации звездного вещества. Оцените радиус R модели нейтронной звезды в виде однородного шара массы M, состоящего из нерелятивистского вырожденного нейтронного газа. Для оценки принять ее массу равной массе Солнца.
Решение. В рассматриваемой модели однородного шара гравитационная энергия звезды выражается формулой , где G – гравитационная постоянная.
Число частиц системы равно 
, где mn – масса нейтрона. Поэтому энергия Ферми вырожденного газа нейтронов выражается формулой
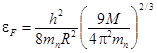. (1)
Кинетическую энергию вырожденного нейтронного газа находим как:
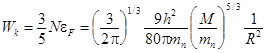. (2)
Складывая гравитационную энергию и кинетическую энергию нейтронного газа (2), находим сумму основных вкладов в полную энергию системы, как функцию ее радиуса R:
. (3)
Здесь введена постоянная R0, значение которой определяется массой звезды. Она равна
. (4)
Условия равновесия системы можно записать как условие минимума энергии:
. (5)
Отсюда находим, что радиус звезды равен постоянной R0.
Подставив в формулу (5) численное значение массы Солнца: M = 2×1030 кг, получаем радиус нейтронной звезды R0 @ 12 км. При этом плотность вещества оказывается колоссальной: 2.5×105 т/мм3, что сопоставимо с плотностью ядерной материи. При больших массах звезда может стать «черной дырой».
Задача 3. Звезды представляют собой массивные раскаленные газовые (плазменные) шары. Оцените, какой должна быть температура однородного изолированного водородного шара, удерживаемого в равновесии собственной гравитацией, если масса и радиус шара имеют такие же значения, как у Солнца (М = 2.0×1030 кг; R = 7.0×108 м).
Задача 4. Оцените радиусы R планет земной группы, предполагая их однородными шарами, состоящими из одинаковых нейтральных атомов с порядковым номером Z и атомной массой A » 2Z. Массы планет M известны. Для оценки принять Z » 20.3.
Задача 5. Сила тяжести ограничивает максимальную высоту рельефа поверхности планеты. Оцените максимально возможную высоту гор на планете массой М и радиусом R. С целью упрощения предположите, что горы имеют форму вертикального цилиндра. Из пород небольшой удельной теплотой плавления l = 130 кДж/кг обладает кремнезем (SiO2).
Задача 6. Известно, что большие астероиды, массы которых превышают 1021 кг, имеют форму близкую к сферической в отличие от астероидов значительно меньшей массы, представляющих собой бесформенные глыбы. Оцените величину массы, при превышении которой астероид принимает сферическую форму, то есть высота рельефа окажется много меньше его радиуса. Плотность вещества принять равной 5×103 кг/м3.
Задача 7. Шаровое скопление звезд содержит обычно сотни тысяч звезд, подобных Солнцу, а радиус скопления составляет примерно 20–30 парсек (1 парсек = 3.086×1016 м). Рассматривая скопление как «газ» из звезд, оцените среднюю квадратичную скорость звезд.
Следующая группа задач связана общим объектом – атмосферой Земли, представленной адиабатической моделью, подробно рассмотренной в работах [1, 3].
Задача 8. Найти зависимости давления, температуры и плотности воздуха от высоты в равновесной изоэнтропной модели земной атмосферы. Изучить их графически.
Решение. В изоэнтропной модели величина удельной энтропии атмосферного газа полагается одинаковой на всех высотах. В случае земной атмосферы такое приближение применимо к ее нижней части – тропосфере. В изоэнтропном (адиабатическом) процессе давление p идеального газа связано с его плотностью r уравнением Пуассона: 
, где s – постоянная, а g – показатель адиабаты, равный отношению теплоемкости газа в изобарном процессе к теплоемкости изохорного процесса.
Давление в атмосфере убывает с увеличением высоты z. Условие равновесия атмосферы можно записать в виде уравнения 
, где g – ускорение силы тяжести. Решив это уравнение совместно с уравнением Пуассона, получаем закон убывания плотности газа с высотой в адиабатической атмосфере:
. (1)
Здесь r0 – плотность воздуха у поверхности земли, а H – максимальная высота адиабатической модели атмосферы (0 < z < H), выражаемая формулой
, (2)
где T0 – абсолютная температура воздуха у поверхности земли, m – молярная масса воздуха, R – молярная газовая постоянная.
Оценим высоту равновесной адиабатической модели атмосферы Земли, приняв температуру воздуха у поверхности земли равной 288 К, а показатель адиабаты g = 1.4. В результате получаем H » 29 км. Этот уровень находится в стратосфере, а тропосфера, высота которой в зависимости от широты составляет от 12 до 18 км, расположена значительно ниже.
Зависимость плотности воздуха от высоты (1) позволяет установить аналогичные зависимости для давления и температуры:
и 
. (3)
Из формул (3) следует, что на максимальной высоте z = H температура обращается в нуль. Это указывает на ограниченность изоэнтропной модели атмосферы.
Графическое изучение высотной зависимости термодинамических параметров по формулам (1) и (3) предлагается студентам провести самостоятельно.
Задача 9. Найти высоту нижней кромки облаков при заданных значениях относительной влажности и температуры воздуха у земли в рамках изоэнтропной модели атмосферы, полагая, что отношение масс влаги и сухого воздуха в единице объема остаются одинаковыми по всей высоте атмосферы. Как изменяется с высотой относительная влажность воздуха?
Указание к решению. Воспользоваться известной зависимостью плотности насыщенного водяного пара от температуры [3].
В ходе решения этой задачи устанавливается, что при повышении влажности высота нижней кромки облаков снижается, увеличение же температуры воздуха, наоборот, ведет к высокой облачности. Эти зависимости предлагается студентам исследовать численно и сравнить результаты расчетов с наблюдениями за состоянием облачности.
Задача 10. Оценить количество влаги, содержащейся в вертикальном равновесном атмосферном столбе с единичной площадью горизонтального сечения при заданных значениях влажности и температуры воздуха у земли. Какая часть влаги в этом столбе находится в конденсированном состоянии?
Указание к решению. Плотность водяного пара убывает с высотой. Если бы не было конденсации водяных паров и последующего выпадения конденсата в виде осадков, то отношение масс паров и сухого воздуха оставалось бы одинаковой по всей высоте атмосферы. Для оценки количества конденсированной влаги в столбе атмосферного воздуха предположить, что конденсированы все водяные пары, удовлетворяющие условиям конденсации.
Задача 11. Вертикальное перемещение воздушного столба может быть вызвано отличием его плотности от плотности окружающего воздуха. Оценить относительное изменение плотности воздуха при изменении его влажности и температуры. Как зависит молярная масса воздуха от влажности и температуры?
Указание к решению. Атмосферный воздух рассматривать как смесь сухого воздуха с неизменными компонентами и водяных паров, содержание которых испытывает заметные изменения, доходя в зависимости от погодных условий до 3–4 % от массы воздуха. Поэтому плотность воздуха при постоянном давлении изменяется с изменением его температуры и влажности, что влияет на динамику атмосферных процессов.
Заключение
Решение подобных задач помогает студентам приобрести навыки теоретического исследования реальных физических систем, а также дает им возможность получать знания о мире в результате активной самостоятельной исследовательской деятельности, а не «принимать к сведению» информацию от преподавателя или иных источников. Способствует формированию профессиональных и общекультурных компетенций, связанных со способностью применять на практике базовые знания по физике, математике и методов теоретического исследования, то есть реализации требований федерального государственного образовательного стандарта к подготовке бакалавра физики.
Результативность предлагаемого дидактического подхода подтверждается тем, что от решения задач-оценок студенты переходят к более детальным исследованиям физических явлений и систем, результаты которых находят отражение в студенческих научных публикациях и выпускных квалификационных работах [1, 7, 8].
Рецензенты:
Стефанова Г.П., д.п.н., профессор, первый проректор – проректор по основной деятельности, ФГБОУ ВПО «Астраханский государственный университет», г. Астрахань.
Коломин В.И., д.п.н., доцент, профессор кафедры общей физики, ФГБОУ ВПО «Астраханский государственный университет», г. Астрахань.