Пусть 
- банахово пространство измеримых и суммируемых с квадратом функций 
. Рассмотрим оператор внутренней суперпозиции 
, определенный равенством (1)
, (1)
где функция 
измерима и 
- положительные фиксированные параметры. При 
этот оператор исследовался многими авторами. В частности известно, что если функция 
ограничена в существенном, то оператор S определен на всем пространстве и ограничен [3]. Кроме того, если 
, и 
то спектр оператора S определяется равенством [1]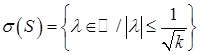 
.
В предлагаемой работе оператор S рассматривается в предположении, что 
. Предварительно рассмотрим вспомогательные утверждения.
Положим
.
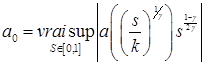Лемма 1. Если 
, то оператор 
определен на всем пространстве 
(то есть 
) и ограничен, причем 
.
Доказательство. Имеем для произвольного 
.
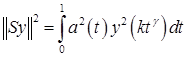Произведя соответствующую замену переменных в интеграле
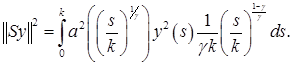
Применим неравенство Гельдера
.
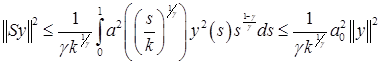Это и означает, что оператор определен на всем пространстве и ограничен. Кроме того, получена требуемая оценка нормы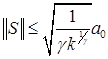 
.
Отметим, что если функция является константой или степенной функцией, то полученная оценка является точной, то есть совпадает с нормой оператора S.
Лемма 2. Оператор, сопряженный к оператору имеет вид
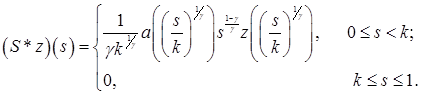
Доказательство. Для произвольных 
рассмотрим
.
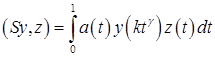Произведем замену переменной в интеграле, полагая 
. Получим
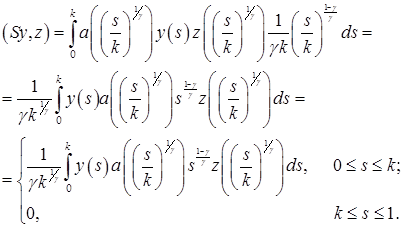
Следовательно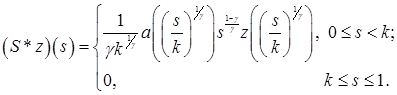 
Следующее утверждение, содержащее информацию о действительной части спектра оператора S, найдет применение в теории функционально-дифференциальных уравнений нейтрального типа.
Теорема 1. Пусть 
и 
. Тогда
.
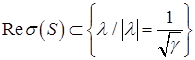Доказательство. Как известно [5], для обратимости линейного оператора 
, где X,Y – (В) – пространства, необходимо и достаточно выполнение в совокупности следующих двух неравенств:
,
,
где 
, 
и m, q – положительные константы.
Для доказательства утверждения теоремы мы установим справедливость неравенств.
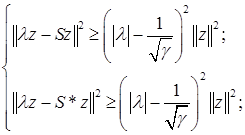
Для произвольного 
. Докажем первое из этих неравенств. Квадрат нормы представим в виде скалярного произведения и преобразуем его.
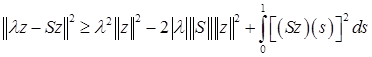(2)
Нетрудно доказать, что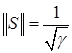 
.
Преобразуем третье слагаемое в правой части (2)
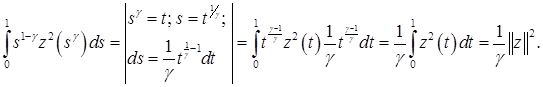
Теперь первое неравенство следует из оценок
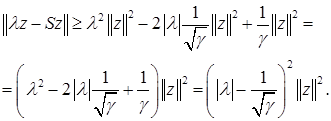
Аналогичным образом доказываем второе неравенство
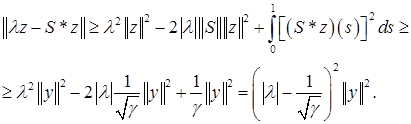
Теорема доказана.
Для исследования квазилинейных операторных уравнений важное значение имеет оценка коэффициента сюрьективности линейного оператора. Напомним, что для линейного оператора , где X,Y – (В) – пространства, рассмотрим числовую характеристику
,
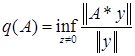называемую коэффициентом сюрьективности. 
оператор сопряженный с А. Воспользуемся свойствами коэффициента сюрьективности, приведенными в работе [2].
Определим сюрьективный спектр оператора А, как множество всех 
, при которых оператор перестает быть сюрьективным. Иными словами, полагаем 
.
Лемма 3. Пусть Х – гильбертово пространство, оператор 
удовлетворяет условию 
, где 
- оператор умножения 
, 
, 
- единичный оператор. Тогда 
.
Доказательство. Так как 
, то очевидно что a – неотрицательная константа.
Спектр положительного оператора 
состоит из одной точки, то есть 
. Теперь используем теорему [4, стр. 440, т. 2].
.
Теорема 2. Пусть . Тогда 
.
Доказательство. Таким образом рассматриваем оператор 
. Кроме того оператор 
имеет вид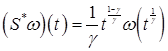 
. Тогда
.
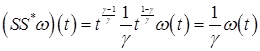В силу леммы 3. Справедливо утверждение теоремы.
Рецензенты:
Плехов О.А., д.ф.-м.н., старший научный сотрудник Института механики сплошных сред Уральского отделения Российской академии наук, г. Пермь.
Гитман М.Б., д.ф.-м.н., профессор кафедры математического моделирования систем и процессов Пермского национального исследовательского политехнического университета, г.Пермь.
Криштоп В.В., д.ф.м.н., профессор, заведующий кафедрой «Физика», Дальневосточный государственный университет путей сообщения, г. Хабаровск, профессор Университета Kwangwoon University, Korea.