Введение
Данные тестов, получаемые при реализации метода функциональных биомеханических проб (ФБМП), представляют собой «оцифрованные» массивы отсчетов сигналов, соответствующих ответным реакциям биообъекта на стандартизованные и дозированные механические воздействия [2]. К сказанному добавим, что описанные данные аналогичны по структуре и форме таким хорошо известным в лечебно-диагностической практике отображениям физиологических процессов, как электрокардиограммы, электронейромиограммы, реограммы, спирограммы и др. При обработке таких данных в медицине давно сложилась практика, при которой их анализ и физиологическая интерпретация осуществляется в несколько этапов.
На первом этапе обычно [6] выделяют и фиксируют качественно определённые фрагменты данных и их количественные параметры и характеристики. Например, на кардиограмме выделяют «зубцы», определяют их высоты, полярность, временные интервалы между ними и т.п.
На втором этапе [7] по системе признаков, определенных требованиями соответствующих методик, выделяют сочетания значений количественных характеристик, измеренных на первом этапе, для отнесения объекта к одному из диагностических классов.
Если объем массивов данных значителен и данные вариативны и повторяются, то возможен третий этап, связанный со статистическим анализом в интересах выявления вероятностных и временных закономерностей наблюдаемого процесса.
Если говорить о методиках обработки биомедицинских данных вообще, то можно констатировать, что современные сертифицированные измерительные средства, используемые в медицине, обеспечивают практически полное подавление основных помех, так что полученные данные можно практически считать детерминированными. Анализ и интерпретация полученных массивов отсчетов сопровождается выделением только некоторых важнейших для диагностики фрагментов. Соответственно, остальные данные игнорируются. Как уже отмечалось, это наиболее характерно для кардиографии, реографии, спирографии. Таким образом, используемые данные избыточны. Действительно, например, при кардиографии, проводимой с использованием цифровой обработки данных, стандартные частоты квантования имеют значения 250, 500 и 750 герц, а суммарная «длина» характерных комплексов QRS, T и P составляет в сумме около 0,3–0,35 сек. Таким образом, для анализа и диагностики используется не более 35% имеющихся отсчетов. Сказанное позволяет понять, почему в процессе эмпирического анализа, проводимого врачом-клиницистом, он использует небольшое число параметров, в среднем равное 7±2, поскольку это число соответствует характерному объему «оперативной» памяти субъекта. Исходя из сказанного, для скрининговых биомеханических проб было бы желательно также использовать небольшое число, характерных для процесса базисных компонент, из которых с достаточной степенью точности можно построить ответ динамической системы на тестовое воздействие.
Поскольку компонентный анализ данных ФБМП имеет конечной целью создание методик массового скринингового обследования, то очевидно, что способы обработки и содержательной интерпретации таких данных должны быть, согласно сложившейся практике, простыми, допускать удобное графическое представление. Все процедуры анализа признаков, объединения (интеграции) данных и их представления врачу-специалисту для принятия решений должны быть в максимальной степени автоматизированы.
Постановка задачи компонентного анализа данных по методу ФБМП
Согласно работам [3, 4, 5], метод ФБМП позволяет получить сигналы, соответствующие ответным реакциям костных элементов и связанных с ними мышц. При этом ответ хорошо разделяется на две части: чисто механическую в виде пассивного движения в ответ на импульс силы и рефлекторную, возникающую вследствие раздражения интерорецепторов сухожилий механическими воздействиями в виде ударов, вибраций и т.п. (например коленный рефлекс). Общий вид ответа на дозированное ударное воздействие представлен на рис.1. По форме первая часть ответа (обозначена стрелками) представляет собой быстро затухающий переходный процесс.
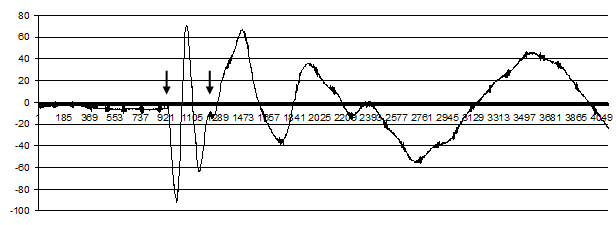
Рис. 1
Исходя из представлений о практически детерминированном сигнале, наиболее адекватным математическим описанием такого сигнала можно считать интерполяционные полиномы, среди которых фундаментальным является степенной полином Лагранжа. Поскольку на практике число полуволн невелико (не более 3-5), то удобно использовать интерполирование полиномом Лагранжа по нескольким равноотстоящим отсчетам.
Общий вид такого полинома можно представить в относительном времени t=n (где n – целое число) выражением:
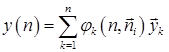 , (1)
, (1)
где ![]() – вектор узлов интерполяции;
– вектор узлов интерполяции;
![]() – вектор значений в узлах интерполируемой функции ответа;
– вектор значений в узлах интерполируемой функции ответа;
![]() – набор степенных интерполирующих функций, таких, что при всех k
– набор степенных интерполирующих функций, таких, что при всех k ![]() при n=nk и равных нулю при n¹nk.
при n=nk и равных нулю при n¹nk.
Интересной особенностью полинома Лагранжа является то, что замена в нём каждого вхождения членов (x–xi), меняющих знак в точках xi на любые другие функции, также меняющие знак в этих точках, приводит к смене базисных функций. Действительно, если jk в выражении (1) представляют собой степенные функции вида:
![]() , (2)
, (2)
где при x¹xk jk=0, а при x=xk jk=1.
Очевидно, что эти условия попадания в узловые точки интерполирования не изменяются, если каждое вхождение (x–xi) и (xk–xi) заменить, например, на sin½(x-xi) и sin½(xk-xi) соответственно. Вместе с тем, осуществится переход к полному ортогональному гармоническому базису. Такой новый многочлен, полученный указанным выше путем, известен как тригонометрический многочлен Гаусса [1].
Неудобство интерполирования полиномами, связанное с преобразованиями дробей вида (2) в общем виде, предлагается преодолеть, используя матричный способ интерполирования, основанный на следующих простых соображениях.
Пусть имеется вектор равноотстоящих отсчетов ![]() . Пусть имеется n базисных функций j0, j1, …,jn , причем каждая из них представлена своим (n–1)–мерным вектором эталонных отсчетов в узлах интерполяции. За эталонные отсчеты базисных функций примем отсчёты в точках x=0,1,2,…,n. Пусть далее вектор
. Пусть имеется n базисных функций j0, j1, …,jn , причем каждая из них представлена своим (n–1)–мерным вектором эталонных отсчетов в узлах интерполяции. За эталонные отсчеты базисных функций примем отсчёты в точках x=0,1,2,…,n. Пусть далее вектор ![]() можно представить как
можно представить как ![]() или в векторно–матричной форме
или в векторно–матричной форме
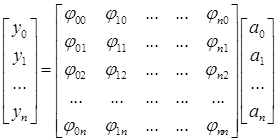 (3)
(3)
где jij (j=0,1,…,n) – эталонный вектор равноотстоящих отсчетов i-й базисной функции.
Записывая (3) в сокращенной форме, получим:
![]() . (4)
. (4)
Если базисные функции заданы и матрица Ф при этом получилась невырожденной (для степенного и гармонического базисов это легко доказать), то вектор коэффициентов разложения ![]() можно найти из (4):
можно найти из (4):
![]() . (5)
. (5)
Выбор порядка интерполирующего полинома определяется порядком системы дифференциальных уравнений движения системы (вязко-упругого) связанных звеньев, состоящей из исследуемой кости (упругого твердого стержня) шарнирно соединённой, как правило, с двумя другими костями (звеньями). Поэтому с учетом присоединенного к исследуемой кости магнитоэлектрического датчика, показания которого U пропорциональны скорости перемещения якоря – ![]() и закона динамики твердого тела, порядок системы дифференциальных уравнений исследуемого объекта не превышает семи. Этому отвечает степенной полином шестого порядка.
и закона динамики твердого тела, порядок системы дифференциальных уравнений исследуемого объекта не превышает семи. Этому отвечает степенной полином шестого порядка.
Построение алгоритма компонентного анализа
Для построения алгоритма компонентного анализа описанного выше интерполированного сигнала необходимо выписать матрицу Ф – базисных векторов седьмого порядка по степеням n. Получим матрицу Ф и обратную ей Ф–1
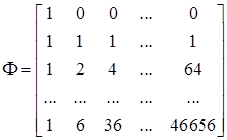 ,
, 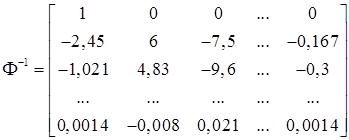 . (6)
. (6)
Выбирая из всего массива отсчетов {yi} семь равноотстоящих на отрезке [0;0,25] секунд, получаем по формуле (5) набор коэффициентов разложения ![]() .
.
Выбор отрезка наблюдения связан с величиной латентного периода сухожильных и других рефлекторных реакций на ударные пробы, который составляет ![]() сек. За это время чисто механический переходный процесс практически заканчивается. Для сопоставления и выбора базиса, обеспечивающего меньшую максимальную ошибку интерполяции, использовался также базисный набор гармонических функций (7), соответствующих интерполяции на основе тригонометрического многочлена Гаусса.
сек. За это время чисто механический переходный процесс практически заканчивается. Для сопоставления и выбора базиса, обеспечивающего меньшую максимальную ошибку интерполяции, использовался также базисный набор гармонических функций (7), соответствующих интерполяции на основе тригонометрического многочлена Гаусса.
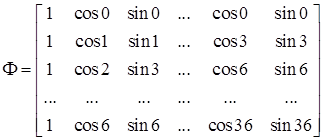 . (7)
. (7)
При этом ниже описаны исследования реального ответа на ударную пробу, представленного на рис. 1.
Применение алгоритма компонентного анализа
Рассмотрим применение алгоритма компонентного анализа к исследованию характеристик сигнала, полученного в результате измерения реакции лучевой кости на дозированное воздействие. Переходный процесс, связанный с механическим ответом, выделенный стрелками на рис. 1, представлен на рис. 2.
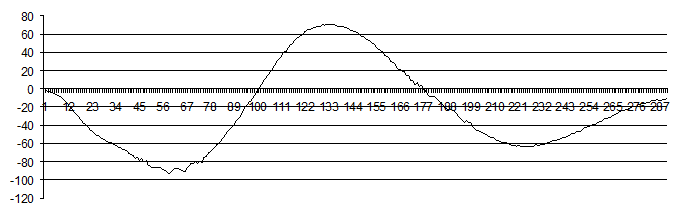
Рис. 2
Начальный отсчет берем при n0=0. Исходя из общей длины сигнала, получаем Dn=48, Dt=3,84 мс, то есть n1=48. Следующие отсчеты берем с шагом Dn=48 отсчётов: n2=96, n3=144, n4=192, n5=240, n6=288. Получаем таблицу следующего вида:
|
N |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
N отсчёта |
0 |
48 |
96 |
144 |
192 |
240 |
288 |
|
Значение |
-3 |
-85 |
-9 |
65 |
-33 |
-54 |
-10 |
Рассчитаем коэффициенты ai при компонентах f0=a0; f1=a1n; f2=a2n2; …, f6= a6n6 с учетом выражения (5): a6=–1,54; a5=26,68; a4=–167,09; a3=447,52; a2=–446,37; a1=–58,8; a0=–3. Используя полученные величины коэффициентов, получаем интерполирующий полином:
![]() . (8)
. (8)
График полученного полинома представлена рис. 3 пунктирной линией. Максимальная ошибка интерполяции составляет 30%.
Используя формулу (5) для случая гармонического базиса (7), аналогично получаем значения коэффициентов разложения ai, bi интерполяционного полинома Гаусса третьего порядка вида (9).
![]() . (9)
. (9)
Эти значения следующие: a0=–20,45, a1=–35,83, b1=3,4, a2=45,18, b2=–25,73, a3=8,1, b3=15,28.
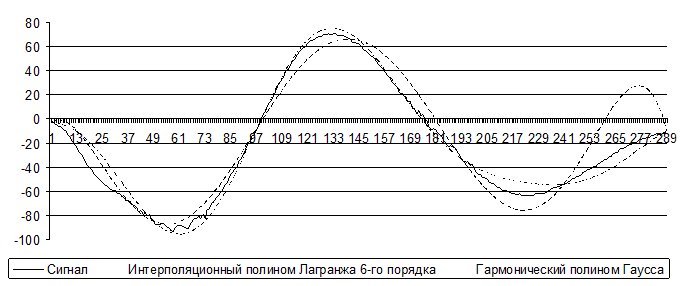
Рис. 3
График интерполирующего тригонометрического многочлена представлен на рис. 3 штрих–пунктирной линией. Как видно из рисунка, максимальная ошибка интерполяции гармоническим полиномом составляет приблизительно 14%, что меньше в 2,15 раза, чем аналогичная ошибка при интерполяции на основе полинома Лагранжа.
Выводы
Описанная выше методика качественного анализа скрининговых функциональных биомеханических проб на основе сокращенной выборки данных позволяет при наличии априорной информации о порядке динамического процесса и подходящем выборе базисного набора функций получить практически приемлемую точность разложения процесса по полному ортогональному базису гармонических функций. Полученное число коэффициентов разложения удобно для качественного анализа и интерпретации результатов проб врачом-клиницистом. Предложенная методика, как показали предварительные исследования, позволяет устанавливать простые связи характера изменения коэффициентов разложения в ai с типовыми патологическими изменениями в костной ткани.
Рецензенты:
Жернаков С.В., д.т.н., профессор, заведующий кафедрой электроники и биомедицинских технологий ФГБОУ ВПО «Уфимский государственный авиационный технический университет» Министерства образования и науки РФ, г. Уфа.
Верхотуров М.А., д.т.н., профессор, профессор кафедры вычислительной математики и кибернетики ФГБОУ ВПО «Уфимский государственный авиационный технический университет» Министерства образования и науки РФ, г. Уфа.



