Введение
Одной из важнейших задач, решаемых в процессе исследования систем управления, является задача идентификации систем. При этом математическая модель может быть определена на основе экспирементальных данных. Наилучшая модель в смысле соответсвия заданным экспериментальным данным выбирается из некоторого класса моделей. Для решения проблемы поиска математической модели используется метод сетевого оператора [1-5].
Метод сетевого оператора для поиска математических выражений использует базисное решение, которое может задаваться на основании опыта исследователя. Такой подход позволяет организовать поиск оптимального решения в окрестности базисного решения.
Метод сетевого оператора позволяет находить оптимальные математические выражения с помощью генетического алгоритма [7]. Генетический алгоритм, также как и нейронные сети, вероятростные методы, которые дополняют друг друга используются для решения задачи оптимизации. Генетический алгоритм использует механизм генетического наследования и естественного отбора. Основными параметрами алгоритма являются количество начальной популяции, число возможно скрещиваемых пар, число поколений, вероятность отбора, скрещивания и мутации. Выбор параметров изменяет эффективность алгоритма.
В настоящей работе проводится исследование выбора базисного решения и выбора параметров генетического алгоритма, чтобы метод сетевого оператора выполнялся эффективно.
Постановка задачи
Расмотрим задачу идентификации системы управления по заданному множеству эксперриментальных данных.
Пусть задано множество эксперриментальных данных:
![]()
где ![]() - вектор входного управления в момент
- вектор входного управления в момент ![]() ,
, ![]() - вектор выходных переменных в момент
- вектор выходных переменных в момент ![]() , M – число точек наблюдения,
, M – число точек наблюдения, ![]() .
.
Необходимо найти модель в виде системы обыкновенных диффиренциальных уравнений
![]() ,
,
где ![]() - искомая функция,
- искомая функция, ![]() - вектор искомых параметров.
- вектор искомых параметров.
Модель должна минимизировать функционалы:
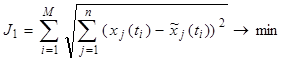 ,
, ![]()
Для решения задачи исползуем метод сетевого оператора.
Метод сетевого оператора
Метод сетевого оператора позволяет строить математические выражении в виде сетевых операторов. Сетевой оператор является ориентированным графом ![]() , где
, где ![]() - множество узлов,
- множество узлов, ![]() - множество дуг или множество упорядоченных пар узлов,
- множество дуг или множество упорядоченных пар узлов, ![]() ,
, ![]() - множество переменных,
- множество переменных, ![]() - множество параметров,
- множество параметров, ![]() - множество унарных операций,
- множество унарных операций, ![]() - множество бинарных операций. Каждый сетевой оператор соответствует определенному математическому выражению.
- множество бинарных операций. Каждый сетевой оператор соответствует определенному математическому выражению.
Для поиска отимального математического выражения необходимо построить множество сетевых операторов ![]() . Для построения множества сетевых операторов
. Для построения множества сетевых операторов ![]() используем базисное решение. Чтобы получить разные решения, необходимо изменять сетевой оператор на основе базисного решения с помощью вектора вариации. Сетевой оператор представляется в виде матрицы
используем базисное решение. Чтобы получить разные решения, необходимо изменять сетевой оператор на основе базисного решения с помощью вектора вариации. Сетевой оператор представляется в виде матрицы ![]() в памяти вычислительной машины. Вектор вариаций записывается как действие оператора на матрицу сетевого оператора
в памяти вычислительной машины. Вектор вариаций записывается как действие оператора на матрицу сетевого оператора
![]()
где ![]() - матрица сетевого оператора после вариации,
- матрица сетевого оператора после вариации, ![]() - вектор вариаций,
- вектор вариаций, ![]() - матрица сетевого оператора до варияции. Для каждого сетевого оператора получается матрица
- матрица сетевого оператора до варияции. Для каждого сетевого оператора получается матрица ![]() в результате вариации базисного сетевого оператора
в результате вариации базисного сетевого оператора ![]() .
.
Для решения задачи поиска отимального математического выражения используем генетический алгоритм, чтобы генерировать различные математические выражения, выбирать и находить отимальное решение на основе оценки его функции пригодности.
Эффективность решения задачи поиска отимального математического выражения зависит от базисного решения, размерности матрицы ![]() , количества векторов вариаций и параметров генетического алгоритма. Рассмотрим вычислительный эксперимент, который показывает зависимость эффективности решения задачи от таких параметров.
, количества векторов вариаций и параметров генетического алгоритма. Рассмотрим вычислительный эксперимент, который показывает зависимость эффективности решения задачи от таких параметров.
Вычислительный эксперимент
Рассмотрим пример для идентификации обьекта по экспериментальными данными, приведенным в таб.1. Исходные даные наблюдаются через интервал ![]() с при управлении
с при управлении ![]() . Порядок системы
. Порядок системы ![]() и размерность управления
и размерность управления ![]() .
.
3.1. Зависимость эффективности решения задачи от базисного решения
Используем метод сетевого оператора. Для решения используем множество унарных операций ![]() и множество бинарных операций
и множество бинарных операций ![]() [2, 3].
[2, 3].
Таб.1. Экспериментальные данные
|
№ |
|
|
|
|
1 |
0 |
1 |
1 |
|
2 |
0.5 |
2.774 |
-0.8404 |
|
3 |
1 |
4.4404 |
0.5103 |
|
4 |
1.5 |
5.231 |
1.7317 |
|
5 |
2 |
5.2213 |
4.0431 |
|
6 |
2.5 |
4.3192 |
6.3385 |
|
7 |
3 |
2.1015 |
8.4114 |
|
8 |
3.5 |
0.1304 |
8.2186 |
|
9 |
4 |
-1.5168 |
6.112 |
|
10 |
4.5 |
-2.246 |
4.5662 |
|
11 |
5 |
-3.1217 |
3.4211 |
|
12 |
5.5 |
-2.3783 |
2.5578 |
|
13 |
6 |
-1.4898 |
1.8829 |
|
14 |
6.5 |
0.64027 |
1.3073 |
|
15 |
7 |
1.8865 |
0.0255 |
|
16 |
7.5 |
3.03 |
1.7591 |
|
17 |
8 |
3.3491 |
2.6049 |
|
18 |
8.5 |
3.2629 |
3.7258 |
|
19 |
9 |
2.7625 |
4.7845 |
|
20 |
9.5 |
1.1507 |
6.0282 |
|
21 |
10 |
0.1916 |
5.4513 |
Для решения задачи использовались следующие параметры генетического алгоритма: размерность популяции – 256, количество скрещиваемых пар в поколении – 64, количество поколений – 256, число поколений между эпохами – 10, длина структурной части хромосомы – 4, число постоянных параметров – 4, количество бит под целую часть параметра – 2, количество бит под дробную часть параметра – 6, вероятность мутации – 0,7, размерность матрицы сетевого оператора – 16.
В первом случае выбираем базисное решение в виде:
![]()
![]()
Базисные значения параметров: ![]() В результате было получено следующее первое решение
В результате было получено следующее первое решение
 .
.
Полученная матрица сетевого оператора соответствует следующему выражению:
![]() ,
,
![]() ,
,
где ![]()
![]()
![]()
![]()
Графики значений полученного выражения приведен на рис. 1 и рис. 2.
Во втором случае выбираем базисное решение в виде:
![]()
![]()
Базисные значения параметров ![]() В результате было получено второе решение:
В результате было получено второе решение:
 .
.
Полученная матрица сетевого оператора соответствует следующим выражениям :
![]()
![]()
где ![]()
![]()
![]()
![]()
Графики значений полученного выражения приведены на рис. 1 и рис. 2.
В третим случае выбираем базисное решение в виде:
![]()
![]()
Базисные значения параметров ![]()
В результате было получено третье решение :
 .
.
Полученная матрица сетевого оператора соответствует следующим выражениям:
![]() ,
,
![]() ,
,
где ![]()
Графики значений полученного выражения приведены на рис. 1 и рис. 2.
Из рисунков видно, что второе базисное решение обеспечивает получение наилучшей аппроксимации экспериментальных данных. Наихудшую аппроксимацию дает решение, полученное на основе третьего базисного решения при одинаковом количестве итераций.
3.2. Зависимость эффективности решения задачи от параметров генетического алгоритма
Для поиска решения используем следующие параметры генетического алгоритма: размерность популяции – 256, количество скрещиваемых пар в поколении – 64, количество поколений – 256, число постоянных параметров – 4, количество бит под целую часть параметра – 2, количество бит под дробную часть параметра – 6, вероятность мутации – 0,7, размерность матрицы сетевого оператора – 16.
Время одного расчета составляло от 2 до 6 часов на ЭВМ с частотой 2,2 ГГц и процессором Intel Core i5. Расчет проводился на программном комплексе NOP4C-I для идентификации систем управления методом сетевого оператора, разработанном на кафедре кибернетики и мехатроники РУДН [6].
Используем базисное решение в виде:
![]()
![]()
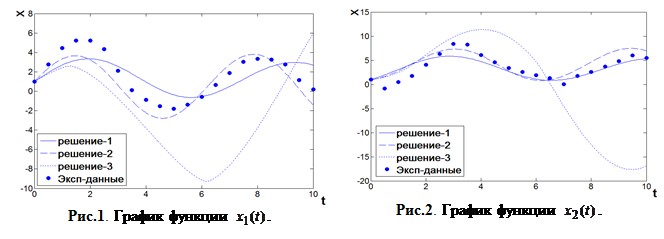
Исследуем зависимость значения функционала качества от числа поколений между эпохами и количеством векторов вариаций в одном возможном решении. Результаты эксперимента приведены в Табл. 2. Графики зависимостей ![]() от количества векторов вариаций для разного числа поколений между эпохами приведены на рис.3 - 6.
от количества векторов вариаций для разного числа поколений между эпохами приведены на рис.3 - 6.
Результаты эксперимента показывают, что при увеличении количества векторов вариаций величина функционала уменьшается приблизительно линейно. Это говорит о том, что выбранные базисное решение и количественные параметры генетического алгоритма не позволили нам приблизиться к предполагаемому минимальному значению функционала.
Таблица 2. Параметры генетического алгоритма
|
№ |
Количество векторов вариаций |
Число поколений в одной эпохе |
Значения функционала |
|
1 |
4 |
10 |
2.53871161 |
|
2 |
4 |
15 |
2.22144046 |
|
3 |
4 |
20 |
2.21971697 |
|
4 |
4 |
25 |
2.21971907 |
|
5 |
8 |
10 |
2.22230944 |
|
6 |
8 |
15 |
2.22230944 |
|
7 |
8 |
20 |
1.97522437 |
|
8 |
8 |
25 |
1.97522437 |
|
9 |
16 |
10 |
2.21913853 |
|
10 |
16 |
15 |
2.19377933 |
|
15 |
16 |
20 |
2.11669991 |
|
16 |
16 |
25 |
2.11669991 |
|
17 |
20 |
10 |
1.98081998 |
|
18 |
20 |
15 |
1.97522437 |
|
19 |
20 |
20 |
1.84972096 |
|
20 |
20 |
25 |
1.81996136 |
|
21 |
24 |
10 |
1.83983297 |
|
22 |
24 |
15 |
1.83552774 |
|
23 |
24 |
20 |
1.81745909 |
|
24 |
24 |
25 |
1.81745909 |
Из таблицы 2 видно, что минимальное значение функционала ![]() 1.81745909 достигается при количестве векторов вариаций равном 24 и числе поколений между сменами эпох равном 20.
1.81745909 достигается при количестве векторов вариаций равном 24 и числе поколений между сменами эпох равном 20.
Матрица сетевого оператора для данного решения имеет вид:

и соответствует математическим выражениям:
![]()
![]() ,
,
где ![]()
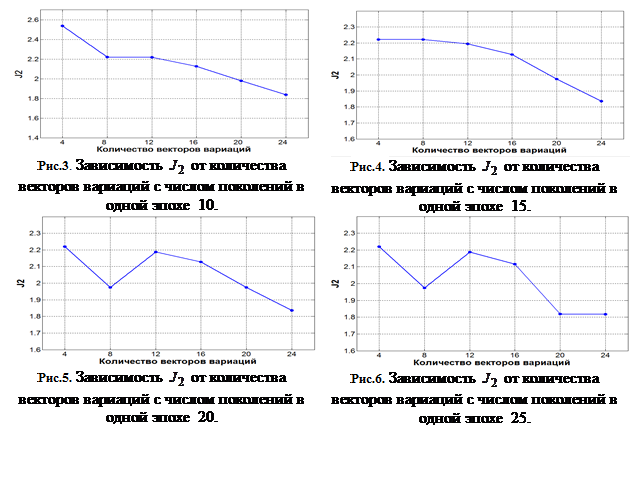
Графики значений полученного выражения приведены на рис. 7 и рис. 8.
На рис. 7. и 8 приведены графики моделирования выбранного решения. Как видно из графиков модель достаточно соответствует заданным экспериментальным данным. Показано, что с использованием количества векторов вариаций равного 24 и числа поколений между сменами эпох равного 20, результат решения поставленной задачи получается более эффективным.
Заключение
Результаты экспериментов показали, что одним из главных этапов метода сетевого оператора является выбор базисного решения. Влияние количественных характеристик генетического алгоритма в методе сетевого оператора на его скорость сходимости принципиально не отличается от других эволюционных алгоритмов.
Работа выполнена по теме гранта РФФИ №13-08-00523-а «Исследование и разработка численного метода идентификации моделей интеллектуальных систем управления»
Рецензенты:
Дикусар В.В., д.ф.-м.н., профессор, главный научный сотрудник ФГБУН Вычислительный центр им. А.А. Дородницына РАН, г. Москва.
Никульчев Е.В., д.т.н., профессор, проректор по научной работе НОУ ВПО Московский технологический институт «ВТУ», г. Москва.



