Введение
Под социальным графом принято понимать граф, моделирующий взаимоотношения между пользователями в Интернете. В отличие от компьютерных сетей, связывающих вычислительные машины, и Всемирной паутины, связывающей гипертекстовые документы, социальный граф связывает между собой людей. С позиции теории анализа социальных сетей [8], социальный граф – это социальная сеть, состоящая из конечного множества единиц социального взаимодействия (акторов) и совокупности связей (отношений) между ними.
Заметим, что в качестве акторов могут выступать как отдельные индивиды, так и социальные группы. В один социальный граф могут входить социальные акторы различных типов, связанные взаимодействиями разного рода и различной степени интенсивности. Люди естественным образом организуются в сети, и взаимоотношения между ними не всегда имеют цифровую природу, например, степень близости интересов или степень заинтересованности сообщества в отдельно взятом вопросе. Одни отношения являются более сильными и интенсивными, чем другие: единомышленники, друзья, коллеги или просто знакомые.
В этой связи все большее число исследователей обращается к математическому аппарату теории нечетких множеств, а также теории нечетких графов и гиперграфов [1] с целью моделирования полного спектра взаимоотношений между социальными акторами. На практике возникает целый ряд прикладных задач, связанных с идентификацией социальных сообществ и социальных позиций [6, 7] в социальной сети и относящихся к классу задач сопоставления с образцом, проверки изоморфизма и распознавания изоморфного вложения графов [3, 4].
Рассмотрим подходы к оценке степени изоморфизма нечетких графов, имеющих социальную природу.
Изоморфизм нечетких графов
Рассмотрим нечеткое отображение Г=(X,Y,F) при условии, что на множестве X задано нечеткое отношение R=(X,P), а на множестве Y – нечеткое отношение S=(Y,Q).
Отображение Г: R→S будем называть гомоморфным отображением или гомоморфизмом между нечеткими отношениями R и S, если для всех xi∈X, i∈I={1,2,...,l} выполняется
Г(R (xi)) ≈ S(Г(xi)), (1)
где Г(xi)∈Y={<
(yk), yk>}, k∈K={1,2,...,m} – множество нечетких образов элементов xi∈X при отображении Г, а знак ≈ является нечетким равенством отношений.
Нечеткое отношение S будем называть отношением, индуцированным гомоморфизмом Г или гомоморфным образом отношения R при отображении Г.
Нечеткий образ Г(<xi, xj>) ребра <xi, xj> отношения R при отображении Г определяется из выражения
Г(<xi, xj>)= {<
<yk, yl>, <yk, yl>>}, (2)
где <yk, yl>=
(mP<xi, xj>&mF<xi, yk>&mF<xj, yl>).
Нечеткий образ петли можно определить как
Г(<xi, xi>)= {<
<yk, yk>, <yk, yk>>}, (3)
где <yk, yk>=
(mP<xi, xi>&mF<xi, yk >).
Выражение для нахождения нечеткого образа Г (R) отношения R представляет собой объединение нечетких образов всех ребер и петель графика P нечеткого отношения R, которое можно представить, как
Г(R)= 
Г(<xi, xj>). (4)
Рассмотрим нечеткое отображение Г=(X,Y,F) при условии, что на области отправления X заданы два или более нечетких бинарных (нечеткий граф) или многоарных (нечеткий гиперграф) отношений, над которыми, в свою очередь, выполняются некоторые теоретико-множественные или алгебраические операции.
Если с точностью до нечеткого равенства отношений сохраняются подобные преобразования над нечеткими образами этих отношений на области прибытия Y отображения Г, то это сохранение свойств преобразования отношений и их образов при переходе от множества X к множеству Y является нечетким гомоморфизмом [2].
Пусть R1 и R2 – произвольные нечеткие отношения, заданные на области отправления X нечеткого отображения Г, а Г(R1) и Г(R2) – их нечеткие образы, определенные на области прибытия Y .
Если для отображения Г выполняется соотношение
Г (R1 ◊ R2) ≈ Г (R1) ◊ Г (R2), (5)
где R1 ◊ R2 – нечеткое отношение на множестве X, представляющее собой результат применения операции ◊ над отношениями R1 и R2, то Г является нечетким гомоморфным отображением или нечетким гомоморфизмом нечетких отношений R1 и R2 по операции ◊.
Отношение Г(R1 ◊ R2) будет являться нечетким гомоморфным образом отношения R1 ◊ R2 на множестве Y при отображении Г.
Если Г – нечеткое инъективное отображение множества X на множество Y и выполняется соотношение (5), то Г является нечетким мономорфизмом отношений R1 и R2 по операции ◊, а Г(R1 ◊ R2) – нечетким мономорфным образом отношения R1 ◊ R2 на множестве Y.
Если Г – нечеткое сюръективное отображение множества X на множество Y и выполняется соотношение (5), то Г является нечетким эпиморфизмом отношений R1 и R2 по операции ◊, а Г(R1 ◊ R2) – нечетким эпиморфным образом отношения R1 ◊ R2 на множестве Y.
Наконец, если Г – нечеткое инъективное и сюръективное отображение множества X на множество Y и выполняется соотношение (5), то Г является нечетким изоморфизмом отношений R1 и R2 по операции ◊, а Г(R1◊R2) – нечетким изоморфным образом отношения R1 ◊ R2 на множестве Y.
По аналогии с методом выявления гомоморфизма нечетких отношений, основанным на установлении факта сохранения их основных свойств [5], можно предложить метод построения гомоморфных образов и определения типа гомоморфизма нечетких отношений по основным теоретико-множественным или алгебраическим операциям, который можно записать в виде следующего алгоритма.
Алгоритм 1
1º. Для каждого из отношений R1 и R2 найти нечеткие образы на отображении Г для всех ребер и петель соответствующих им графов, используя выражения (2), (3), а также нечеткие образы отношений R1 и R2 с помощью выражения (4).
2º. Определить отношения, являющиеся результатом выполнения заданных операций ◊ над исходными отношениями R1 и R2 и над их нечеткими образами Г(R1) и Г(R2).
3º. Пользуясь выражением (5), вычислить значения степеней нечеткого равенства для каждой из заданных операций. Если степень нечеткого равенства отношений, полученных в (1), больше или равна 0,5, то считать факт существования гомоморфизма нечетких отношений R1 и R2 по операции ◊ установленным.
4º. Определить тип нечеткого гомоморфизма, пользуясь формулами инъективности и сюръективности отображения Г:
b(Г)inj =1- 
(
((y)& 
(y))),
b(Г)sur=
(
(
(x))).
Понятие нечеткой клики
Рассмотрим ориентированный или неориентированный нечеткий граф 
.
Определение 1. Подмножество вершин 
назовем нечеткой кликой со степенью
Величина δ(X') отражает степень близости подграфа 
к полному подграфу с X' вершинами.
Определение 2. Подмножество вершин назовем максимальной кликой со степенью 
, если справедливо:
Иначе говоря, любое подмножество 
, включающее в себя подмножество 
, является кликой со степенью меньшей величины 
.
Рассмотрим семейство всех максимальных нечетких клик 
, содержащих ровно k вершин со степенями 
соответственно.
Введем обозначение 
. Как и в случае нечетких внутренне устойчивых множеств, если семейство 
, то положим 
. Величина 
означает, что в графе 
существует k-вершинный подграф, в котором между любыми двумя вершинами существует ребро со степенью не менее и не существует никакого другого подграфа с k вершинами, чья степень была бы больше величины .
Определение 3. Множество 
назовем нечетким множеством клик нечеткого графа 
.
Свойство 1. Из определения 3 непосредственно вытекает неравенство: 
.
Заметим, что величина 
равна 0, если любой k-вершинный подграф имеет хотя бы одну пару вершин, например 
, между которыми нет никакого ребра, то есть 
.
Рассмотрим метод нахождения всех максимальных нечетких клик и нечеткое множество клик нечеткого графа , в котором:
.
Свойство 2. Семейство максимальных нечетких клик исходного графа совпадает с семейством максимальных нечетких внутренне устойчивых множеств дополнительного графа 
.
Данное свойство непосредственно вытекает из определения максимальной нечеткой клики и максимального нечеткого внутренне устойчивого множества.
Из свойства 2 непосредственно вытекает такое следствие.
Следствие 1. Нечеткое множество клик нечеткого графа совпадает с нечетким множеством внутренней устойчивости дополнительного графа .
На основании свойства 2 и следствия 1 предложим следующий метод нахождения максимальных нечетких клик и максимального нечеткого внутренне устойчивого множества нечеткого графа:
- по заданному нечеткому графу 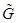строим дополнительный граф
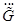; - для графа 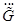находим семейство максимальных нечетких внутренне устойчивых множеств с соответствующей степенью внутренней устойчивости;
- полученное семейство одновременно является и семейством максимальных нечетких клик исходного графа;
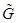- по вычисленному семейству максимальных нечетких клик определяем нечеткое множество клик
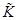нечеткого графа [1].
Оценка степени изоморфизма на основе нечетких клик нечетких графов
Пусть 
и 
– нечеткие графы, изоморфные со степенью f.
Обозначим через
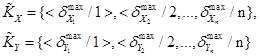
нечеткие множества клик графов 
и 
соответственно. Тогда справедливы следующие свойства.
Свойство 3. Справедливо неравенство
.
Данное свойство непосредственно вытекает из определения ядер нечеткого графа.
Свойство 4. Справедливо неравенство
.
Учитывая взаимосвязь между нечетким множеством клик рассматриваемого графа и нечетким множеством внутренней устойчивости дополнительного графа, свойство 4 доказывается аналогично.
Пример 1. Рассмотрим пример оценки степени изоморфизма нечетких графов и , для которых определены нечеткие множества клик
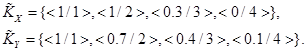
Степень изоморфизма рассматриваемых графов можно оценить с помощью выражения
.
Степень изоморфизма указанных нечетких графов на основе анализа нечетких клик не будет превышать значения 0.7.
Заключение
Предложенные методы и алгоритмы оценки степени изоморфизма нечетких графов на основе нечетких клик можно применять для решения целого ряда прикладных задач, связанных с идентификацией социальных сообществ и социальных позиций в социальной сети. На следующем этапе планируется дать теоретическую и экспериментальную оценку вычислительной сложности алгоритмов на реальных примерах больших социальных сетей.
Работа выполнена в рамках гранта Южного федерального университета № 213.01-24/2013-79 «Разработка и исследование методов нечетко-множественного анализа и моделирования социальных графов».
Рецензенты:
Карелин В.П., д.т.н., профессор, заведующий кафедрой прикладной математики и информационных технологий НОУ ВПО «Таганрогский институт управления и экономики», г. Таганрог.
Финаев В.И., д.т.н., профессор, заведующий кафедрой систем автоматизированного управления ФГАОУ ВПО «Южный федеральный университет», г. Ростов-на-Дону.