Стратегический процесс в организации, в конечном итоге, представляет собой процесс постановки (формирования) и реализации стратегических целей.
Наибольшую сложность в стратегическом процессе традиционно вызывает этап реализации стратегии. При разработке моделей поддержки процессов принятия стратегических решений нужно осознавать, какова степень достижения цели в тот или иной момент времени (при тех или иных значениях показателей).
Степень достижения цели можно рассматривать как полезность для организации (или ее отдельных подразделений), полученную в результате осуществления соответствующих стратегических мероприятий, следовательно, формализацию зависимости между уровнями достижения цели (УДЦ) и значениями соответствующих показателей можно рассматривать как нахождение некоторой функции полезности [3].
Такая постановка задачи уже встречается в научной литературе. Можно выделить два основных направления исследований в этой области. В рамках одного из направлений авторы применяют различные методы агрегирования показателей, а затем получают зависимость УДЦ от агрегата. Другое направление связано с нахождением прямой функциональной зависимости между показателями и УДЦ.
В рамках второго направления задача решена для различных видов показателей (зависимых, односторонне независимых, независимых) [3, 4, 5]. Однако во всех предложенных решениях присутствуют ограничения для области значений показателей, т.е. область ограничений функции заключена между начальными и целевыми значениями показателей. На практике встречаются ситуации, когда при выполнении нескольких (или даже одного) стратегических мероприятий целевые значения показателей могут быть превышены. Предложенные методы в таких ситуациях не дают ответа на вопрос, что происходит с полезностью для организации. В таких условиях функция полезности может принимать отрицательные значения.
Впервые знакопеременная функция полезности была получена американскими исследователями Кини и Райфа [2] на основе лотерей и предназначалась для экономических показателей: отрицательной области соответствовали убытки предпринимателя [1].
Данная статья посвящена методу нахождения функции, значениями которой являются уровни достижения цели (УДЦ), описанной двумя показателями. Нормированные значения этих показателей будут являться аргументами данной функции.
В дальнейшем будем использовать следующие обозначения:
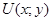– функция зависимости УДЦ от показателей цели 
, 
; 
, 
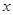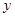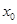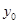– начальные значения показателей; 
, 
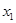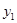– целевые значения показателей; 
, 
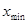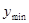– минимально возможные значения показателей 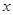и ; 
, 
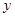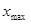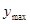– максимально возможные значения показателе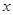й и .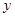
В частном случае минимальные значения , и начальные значения , могут совпадать.
Пусть рассматриваемая нами функция достигает своего максимума в единственной точке. При этом будем полагать, что при превышении целевых значений показателей функция полезности начинает убывать.
В соответствии с принятыми нами обозначениями введем следующие предположения:
- функция
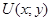непрерывна на всей области определения; - область значений функции 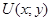есть отрезок
; 
; 
; 
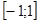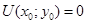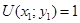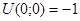; - на области
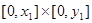функция 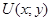возрастает по каждой переменной; - на области
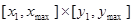функция 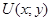убывает по каждой переменной.
Координатное поле, в котором располагаются изолинии (кривые безразличия функции ), представлено на рисунке 1.
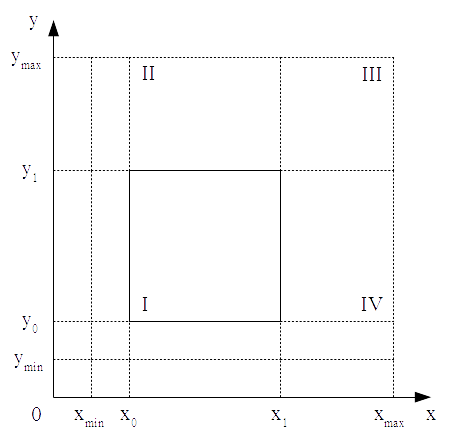
Рисунок 1. Координатное поле области определения функции полезности
Как видно из рисунка 1, область 
разбита на шестнадцать прямоугольных областей. В рамках поставленной задачи нас в первую очередь интересуют области, где значения обоих показателей превышают начальные. Для удобства пронумеруем такие области.
Для рассматриваемого случая под «полезным» приростом здесь и в дальнейшем будем понимать положительный прирост показателя на отрезке от начального значения до целевого (в этом случае полезность возрастает). «Вредный» прирост – это положительный прирост показателя на отрезке от целевого значения до максимально возможного (в этом случае полезность убывает). Область I представляет собой прямоугольник, где оба показателя и имеют «полезный» прирост по сравнению с начальными значениями.
Для областей II и IV характерен «полезный» прирост одного из показателей (в области II по , в области IV по ) и «вредный» прирост второго. В области III происходит «вредный» прирост обоих показателей.
Для дальнейшего решения поставленной задачи введем ряд предположений об изолиниях искомой функции полезности:
- изолинии являются замкнутыми непрерывными кривыми;
- изолинии являются кусочно-гладкими. Гладкость может нарушаться только на границах областей;
- в областях I и III изолиния как функция
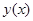не возрастает; - в областях II и IV изолиния как функция 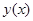не убывает;
- направление выпуклости изолинии может меняться (т.е.
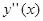меняет знак) только на границах областей.
В ситуации, когда имеют место описанные нами ограничения, может быть применена модификация метода, описанного в работе [3]. Необходимость модификации связана с тем, что указанный метод позволяет получить значение целевой функции только в области от начальных значений показателей до целевых (область I в принятых нами обозначениях). Ещё одним недостатком прямого применения указанного метода является существенный рост количества точек, которые необходимо найти для построения искомой зависимости. От количества искомых точек напрямую зависит количество вопросов, на которые эксперту необходимо дать ответ. При увеличении количества показателей, описывающих цель, эта проблема становится всё более существенной, так как большое количество вопросов может утомить эксперта, а это, в свою очередь, может сказаться на качестве ответов и/или на сроках формирования итоговой карты целей и списка стратегических мероприятий.
В соответствии с указанным методом найдем кривые безразличия для функции полезности в области I. В результате экспертного опроса сначала будут получены граничные точки для искомых изолиний. Следует заметить, что граничные точки, которые лежат на границе области I и области II, а также на границе области I и области IV, можно будет использовать для нахождения продолжения изолинии с соответствующим уровнем полезности в областях II и IV.
Далее нужно достроить изолинию в областях II и IV. Возможное место расположения граничных точек в этих областях отличается от возможного расположения граничных точек в областях I и III. В областях I и III левые граничные точки могут быть расположены на левой и/или на верхней границе, а правые точки – на правой и/или нижней границе. В областях II и IV левые граничные точки могут быть расположены на левой и/или на нижней границе, а правые точки – на правой и/или верхней границе. Такое расположение граничных точек связано с введенными нами предположениями об изолиниях функции полезности.
Граничные точки, лежащие на границах области III с областями II и IV, также можно использовать для нахождения изолиний в области III. Такой подход позволяет снизить количество вопросов, задаваемых эксперту.
Первым приближением кривых безразличия являются отрезки, соединяющие граничные точки с одинаковым уровнем полезности в соответствующих областях. Для повышения точности интерполяции функции необходимо аппроксимировать кривые безразличия ломаными. Для этого нужно определить дополнительные точки, значение полезности в которых будет равно значению в граничных точках. Способ аппроксимации описан в работе [2].
Для оценки значения функции полезности в произвольной точке области используются минимальные расстояния от этой точки до ломаных, между которыми она находится. Расчет происходит по следующей формуле:
,
где 
– порядковый номер ломаной;
, 
– расстояния до соответствующих ломаных;
, 
– значения функции полезности в соответствующих ломаных.
При расчете значения по данной формуле используются ломаные той области, в которой находится заданная точка. При этом в области I в качестве ломаных выступают еще и точки 
, 
, в области II – 
, , в области III – , 
, в области IV – , 
.
Рецензенты:
Мазелис Л.С., д.э.н., директор института информатики, инноваций и бизнес-систем, заведующий кафедрой математики и моделирования, ФГБОУ ВПО «Владивостокский государственный университет экономики и сервиса», г. Владивосток.
Солодухин К.С., д.э.н., профессор кафедры математики и моделирования, заведующий лабораторией стратегического планирования, ФГБОУ ВПО «Владивостокский государственный университет экономики и сервиса», г. Владивосток.