Введение
Семантические сети являются универсальной структурной моделью формализации процесса принятия решений [7]. Особенность семантической сети как модели заключается в целостности системы поиска решений, выполненной на ее основе, позволяющей не разделять базу знаний и механизмы выводов [5].
Базовым функциональным элементом семантической сети служит структура, состоящая из узлов и связывающих их дуг. Каждый узел представляет некоторое понятие, а дуга – отношение между парами понятий. Каждая такая пара отношений определяет некоторое утверждение, являющееся функциональным элементом семантической сети. Узлы помечаются именами соответствующего отношения.
Дуги имеют направленность, благодаря чему между понятиями в рамках некоторого утверждения определено отношение типа «субъект – объект». Каждый узел может быть соединен с любым числом других узлов, в результате чего обеспечивается формирование сети утверждений.
С позиции алгебры логики базовую структуру семантической сети можно рассматривать в качестве эквивалента предиката (дуги) с двумя аргументами (узлами). При выборе различных обозначений для описания отношений можно представлять самые различные совокупности утверждений.
При описании ситуаций в виде семантических сетей особый практический интерес имеет связь вида «являться», отражающая принадлежность объекта к некоторому классу. К другим видам связей, нашедшим конкретное применение при отражении общих представлений об объекте, относятся связи: вида «иметь», указывающая на то, что один объект представляет часть другого, и вида «есть», указывающая на то, что одно понятие служит атрибутом другого. Пользуясь подобными отношениями, можно представлять иерархические совокупности утверждений. Из утверждений можно строить различные иерархические структуры, увеличивая количество понятий и связей. Иерархия, построенная на основе наследования свойств, обеспечивает эффективный способ представления знаний, сокращающий объем информации, которая требуется для описания каждого конкретного утверждения. Это дает возможность упростить процесс обработки знаний, а также извлекать нужную информацию с помощью запросов.
Поиск оптимальных решений с использованием нечетких семантических сетей
При функционировании систем представления знаний на основе семантических сетей используется поисковый режим, где запрос можно представить социальным графом, в котором вершины-акторы заранее не определены.
Выделяют два основных типа запросов: на существование и на перечисление. Запрос на существование не содержит переменных и предусматривает ответ типа «да», если изоморфное вложение графа запроса в семантическую сеть удалось найти, и «нет» в противоположном случае. При обработке перечисляющего запроса происходит поиск всех возможных изоморфных графу запроса подграфов в семантической сети, а также конкретизация переменных.
Частным случаем нечеткой семантической сети, описывающей некоторую совокупность объектов или явлений (ситуаций), является семантическая сеть, рассмотренная в [2].
Здесь нечеткая семантическая сеть представлена в виде ориентированного социального графа 
где 
– множество вершин – концептов (признаки, свойства, значения, факторы), 
– множество вершин – объектов (ситуации, заключения), 
– множество взвешенных ориентированных ребер 
- функция на ребре 
, определяющего для ребер 
– степень 
наличия данного свойства (признака, значения) 
ситуации (объекта) 
, а для ребер - силу 
семантической ассоциации между концептами 
и 
. Здесь 
. Связи между вершинами из могут соответствовать различным видам отношений или типам взаимодействия и определяются как неопределенно транзитивные, т.е. если имеются 
и 
, то
.
Из этого определения следует, что сила связей вершин 
задана силой наиболее слабой связи. Социальный граф 
строится экспертом данной предметной области и позволяет в сжатом виде описывать либо все множество объектов или ситуаций ПР, либо лишь эталоны – представители классов ситуаций. Социальный граф задает нечеткое отношение включения на множестве вершин 
.
Запрос, по которому осуществляется вывод (поиск соответствующего объекта или ситуации), представляет в общем случае нечеткое подмножество концептов (признаков), заданных значениями степени принадлежности, описывающих некоторую текущую ситуацию или объект, подлежащий классификации (поисковый образ).
Логический вывод сводится к определению пути с максимальной оценкой между вершиной – запросом Z, соответствующей классифицируемой ситуации, и всеми вершинами – объектами (заключениями) 
на социальном графе 
, образованном присоединением вершины Z, соответствующей текущей ситуации, к социальному графу , задающему поле знаний. При этом присоединяемая вершина Z соединяется с вершинами – концептами 
, ориентированными ребрами 
, с весами 
, соответствующими степеням принадлежности конкретного концепта (признака, свойства, фактора) в описании исходной (классифицируемой) ситуации (поискового образа). Степень соответствия 
некоторого объекта (заключения, ситуации) 
, определяется оценкой пути, полученного в результате логического вывода.
Рассмотренная модель применяется в тех случаях, когда необходимо определить принадлежность текущей ситуации к тому или иному классу ситуаций или же для некоторой желаемой ситуации найти ближайшую из множества реально имеющихся в базе данных. Очевидно, что в обоих случаях приходится вычислять степень нечеткого сходства сравниваемых ситуаций. Под нечетким сходством здесь будем понимать отношение нечеткого включения, обладающее свойством транзитивности [3]
.
Следует отметить, что наличие семантически обусловленных ассоциативных связей между признаками позволяет уточнять описание ситуаций и тем самым способствовать повышению правдоподобности модели.
В частности (рис. 1), если признак не вошел в описание ситуации у, но ассоциативно связан с признаком 
, вошедшим в описание у , где 
то это означает, что в социальном графе отсутствует ребро 
, но присутствуют ребра 
т.е. 
В силу транзитивности можно в граф ввести ребра 
с весом
Если же в социальном графе имеется еще одна вершина 
, связанная с вершиной у ребром с весом 
, а с вершиной – ребром с весом 
то в социальный граф можно ввести ребро с весом
Рис. 1. Пример наличия семантически обусловленных ассоциативных связей
Вводя дуги на основе свойства транзитивности, мы фактически применяем операцию транзитивного замыкания.
Воспользовавшись ею, можно отобразить лишь зависимость вершин у от x и исключить зависимость между вершинами 
. В результате получим социальный граф нечеткого соответствия, показанный на рис. 2.
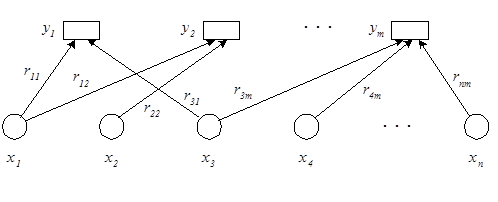
Рис. 2. Граф нечеткого соответствия
Процедура нахождения транзитивного замыкания нечеткого отношения включения выполняется в результате последовательного осуществления операций максиминной композиции матрицы смежности R социального графа и матрицы 
, где 
1, 2, …, и операции объединения по формуле
.
Причем, если для некоторого 
имеем 
, то
[3]. (1)
Результат операции 
определяется функцией принадлежности
(2)
Процедура нахождения транзитивного замыкания 
нечеткого отношения включения 
позволяет установить степень принадлежности 
концепта (признака, свойства, фактора) , ранее не входившего в описание ситуации . Если же концепт входит в описание ситуации , т.е. существует ребро , то наличие ассоциативной связи с и связи с позволяет уточнить вес ребра по формуле
Это дает возможность с большей точностью определять степень нечеткого сходства ситуаций и, соответственно, находить более адекватное решение.
Способы определения значения нечеткой релевантности
Процедуры сравнения нечетких описаний искомого объекта (ситуации) и эталонных объектов, хранящихся в базе знаний, лежат в основе построения интеллектуальных информационно-поисковых систем [6], систем принятия решений на основе определения сходства ситуаций [1], ситуационных советующих систем [4] и т.п.
Рассмотрим более подробно способы определения значения нечеткой релевантности (степени нечеткого сходства) классифицируемой текущей ситуации (поискового образа, запроса) и ситуации, хранящейся в базе знаний при работе с нечеткой семантической сетью.
Чтобы описать правила вывода для поиска, введем следующие предикаты [8]:
Z(z,x) – «запрос z описывается концептом x»; Y(y,x) – «ситуация y описывается концептом x»; L(xi,xj) – «концепт xi связан ассоциативно с концептом xj»; RX(y,x) – «ситуация y релевантна концепту x»; RX(y,z) – «ситуация y релевантна запросу z»; RZX(z,x) – «запрос z релевантен концепту x». Значение истинности для этих предикатов варьируется в интервале [0;1]. В дальнейшем, без потери общности, будем полагать, что запрос описывается лишь одним концептом, хотя на самом деле он описывается несколькими концептами из множества . Предлагается следующее правило поиска:
.
Если запрос 
и ситуация 
описываются концептом 
, то данная ситуация считается релевантной концепту . Правило ограничивает рамки возможных значений 
истинности предиката 
интервалом, заданным
. (3)
Затем поиск расширяется по сети, начиная с концепта , в соответствии с правилом:
Даже если ситуация не описывается концептом , ситуация считается настолько релевантной , насколько существует связь между и , а описывается концептом . Это ограничивает возможное значение истинности предиката 
интервалом
. (4)
Для каждого концепта из множества
, связанного с концептом существуют значения 
истинности, выведенные по последнему правилу. Задавая
получим 
.
Для определения релевантности ситуации 
концепту 
используется соотношение
. (5)
В большинстве случаев запрос (классифицируемая ситуация) описывается несколькими концептами (признаками), множество которых можно обозначить через 
. Для каждого концепта 
получают значение релевантности 
и задают значение 
.
Эти значения используются для оценки общей релевантности d ситуации у запросу z. Если предполагать, что концепты не соединены связками и/или, то можно использовать усредненную функцию
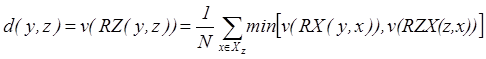(6)
Данный запрос z на базе правил поиска и определения релевантности позволяет в качестве решения (результата поиска) получить множество 
ситуаций, релевантных , как нечеткое подмножество множества 
всех ситуаций.
(7)
С целью ограничения множества релевантных ситуаций величиной релевантности 
можно взять уровень , и тогда получим нечеткое множество ситуаций.
.
Формализация процедур оценки релевантности всех концептов ситуации реализуется при помощи рассмотренной выше процедуры получения транзитивного замыкания матрицы смежности (нечеткого отношения) для исходного нечеткого социального графа (нечеткой семантической сети).
В результате для каждой ситуации получаем нечеткое подмножество
концептов, описывающее ситуацию , где
.
С другой стороны, запрос (классифицируемая ситуация) также нечетко описывается концептами и задается нечетким множеством
.
Определение значения релевантности (степени нечеткого сходства) 
ситуации запросу осуществляется по формуле (6). Будем называть рассмотренный способ оценки релевантности методом минимального значения.
Заключение
В результате анализа методов формализации процессов принятия решений предложена модель поиска оптимальных решений с использованием нечеткой семантической сети, основанная на определении степени принадлежности текущей ситуации к тому или иному классу эталонных ситуаций на основе степени нечеткого сходства, где под нечетким сходством понимается отношение нечеткого включения, обладающее свойством транзитивности.
Работа выполнена в рамках гранта Южного федерального университета № 213.01-24/2013-79 «Разработка и исследование методов нечетко-множественного анализа и моделирования социальных графов».
Рецензенты:
Гуда А.Н., д.т.н., профессор, проректор по научной работе, зав. кафедрой «Информатика» ФГБОУ ВПО «Ростовский государственный университет путей сообщения», г. Ростов-на-Дону.
Курейчик В.В., д.т.н., профессор, заведующий кафедрой систем автоматизированного проектирования ФГАОУ ВПО «Южный федеральный университет», г. Ростов-на-Дону.