В данной работе мы рассмотрим еще один метод выбора стратегий взаимодействия вуза со стейкхолдерами, основанный на определении детерминированного эквивалента. Как говорилось в работах [1-3], для каждого из сценариев отношений вуза с группой заинтересованных сторон (ГЗС) могут быть найдены весовые коэффициенты целесообразности применения различных типов стратегии вуза по отношению к ГЗС. Выбор типа стратегии взаимодействия вуза с каждой ГЗС осуществляется на основе анализа характеристик отношений [7-9]. Анализ характеристик отношений между вузом и некоторой ее ГЗС может показать наличие нескольких возможных ситуаций, каждой из которых может быть поставлен в соответствие определенный (наиболее подходящий) тип стратегии взаимодействия: удовлетворение запросов, защита, воздействие или сотрудничество. Для того чтобы определить, какую стратегию следует применять к данной ГЗС в сложившейся ситуации, каждой из стратегий ставится в соответствие весовой коэффициент, отражающий целесообразность ее применения (к этой ГЗС в данной ситуации).
Каждый коэффициент представляет собой значение некоторой функции, аргументами которой являются те или иные характеристики отношений, а область значений – промежуток от 0 до 1. При этом каждая функция должна принимать максимальное значение в случае, когда соответствующие характеристики отношений достигают своих предельных значений для соответствующего случая.
Весовые коэффициенты ![]() (
(![]() ), отражающие целесообразность применения в отношении
), отражающие целесообразность применения в отношении ![]() -й ГЗС стратегии
-й ГЗС стратегии ![]() -го типа, рассчитываются по формулам:
-го типа, рассчитываются по формулам:
![]() ,
, ![]() ,
, ![]() ,
, ![]() , (1)
, (1)
где ![]() ,
, ![]() - степени желания изменений
- степени желания изменений ![]() -й ГЗС в отношении вуза и вуза в отношении
-й ГЗС в отношении вуза и вуза в отношении ![]() -й ГЗС;
-й ГЗС; ![]() - количественная оценка власти между вузом и
- количественная оценка власти между вузом и ![]() -й ГЗС.
-й ГЗС.
Рассмотрим тот же самый пример, который рассматривался авторами в работе [4], и примем решение о выборе стратегии взаимодействия вуза с группой стейкхолдеров с помощью детерминированного эквивалента. В таблице 1 представлена целесообразность применения типов стратегий взаимодействия вуза с клиентами.
Таблица 1 – Целесообразность применения типов стратегий взаимодействия вуза с клиентами
|
Сценарии (вероятности) |
Типы стратегий взаимодействия |
|||
|
Удовлетворение запросов |
Защита |
Воздействие |
Сотрудничество |
|
|
Сценарий 1 (0,3) |
0,57 |
0,61 |
0,47 |
0,6 |
|
Сценарий 2 (0,23) |
0,71 |
0,43 |
0,61 |
0,43 |
|
Сценарий 3 (0,18) |
0,46 |
0,62 |
0,36 |
0,6 |
|
Сценарий 4 (0,15) |
0,54 |
0,72 |
0,44 |
0,5 |
|
Сценарий 5 (0,09) |
0,5 |
0,67 |
0,4 |
0,63 |
|
Сценарий 6 (0,05) |
0,55 |
0,73 |
0,45 |
0,56 |
Как видно из таблицы, выбор типа стратегии взаимодействия происходит в рамках различных сценариев отношений между вузом и группой стейкхолдеров. При этом каждому типу стратегии поставлена в соответствие целесообразность применения для различных сценариев.
Вначале введем некоторые определения. Будем рассматривать случайную величину 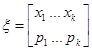 , где
, где ![]() ,
, ![]() как лотерею с выигрышами
как лотерею с выигрышами ![]() , в которой
, в которой ![]() – доля билетов с выигрышами
– доля билетов с выигрышами ![]() (
(![]() ). В нашем случае, поскольку при выборе типа стратегии лицо принимающее решение (ЛПР) не знает, в рамках какого сценария будут выстраиваться отношения вуза с группой стейкхолдеров, то в качестве лотерей будем рассматривать типы стратегий взаимодействия. Под
). В нашем случае, поскольку при выборе типа стратегии лицо принимающее решение (ЛПР) не знает, в рамках какого сценария будут выстраиваться отношения вуза с группой стейкхолдеров, то в качестве лотерей будем рассматривать типы стратегий взаимодействия. Под ![]() и
и ![]() будем рассматривать целесообразности применения типов стратегий и вероятности сценариев соответственно.
будем рассматривать целесообразности применения типов стратегий и вероятности сценариев соответственно.
Таким образом, рассмотрим четыре типа стратегии (лотереи): ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Для выбора наиболее оптимального типа стратегии взаимодействия необходимо для каждого типа стратегии определить детерминированный эквивалент (ДЭ). Под детерминированным эквивалентом типа стратегии взаимодействия будем рассматривать целесообразность применения типа стратегии при абсолютно вероятном сценарии (
. Для выбора наиболее оптимального типа стратегии взаимодействия необходимо для каждого типа стратегии определить детерминированный эквивалент (ДЭ). Под детерминированным эквивалентом типа стратегии взаимодействия будем рассматривать целесообразность применения типа стратегии при абсолютно вероятном сценарии (![]() =1), которая для ЛПР эквивалентна (равноценна) принятию данного типа стратегии взаимодействия в условиях неопределенности (т.е. ЛПР не знает в рамках какого сценария будут выстраиваться отношения вуза с группой стейкхолдеров). Выбор будет осуществляться ЛПР в пользу такого типа стратегии взаимодействия, которому будет соответствовать наибольший детерминированный эквивалент.
=1), которая для ЛПР эквивалентна (равноценна) принятию данного типа стратегии взаимодействия в условиях неопределенности (т.е. ЛПР не знает в рамках какого сценария будут выстраиваться отношения вуза с группой стейкхолдеров). Выбор будет осуществляться ЛПР в пользу такого типа стратегии взаимодействия, которому будет соответствовать наибольший детерминированный эквивалент.
Чтобы определить детерминированный эквивалент типа стратегии взаимодействия, можно воспользоваться следующим алгоритмом [5].
Шаг 1. Построить по заданному типу стратегии взаимодействия ![]() тип стратегии взаимодействия в полезностях
тип стратегии взаимодействия в полезностях ![]() . Для этого надо в типе стратегии взаимодействия
. Для этого надо в типе стратегии взаимодействия ![]() заменить каждую целесообразность применения типа стратегии
заменить каждую целесообразность применения типа стратегии ![]() на ее полезность
на ее полезность ![]() .
.
Шаг 2. Найти ожидаемую полезность ![]() типа стратегии взаимодействия
типа стратегии взаимодействия ![]() по формуле:
по формуле:
![]() . (2)
. (2)
Шаг 3. От точки ![]() , лежащей на оси ординат, «перейти» через кривую эквивалентов на ось абсцисс. Полученная точка
, лежащей на оси ординат, «перейти» через кривую эквивалентов на ось абсцисс. Полученная точка ![]() и будет детерминированным эквивалентом типа стратегии взаимодействия.
и будет детерминированным эквивалентом типа стратегии взаимодействия.
Воспользуемся вначале критерием математического ожидания. Для стратегии удовлетворения запросов ![]() 0,57; для стратегии защиты
0,57; для стратегии защиты ![]() 0,6; для стратегии воздействия
0,6; для стратегии воздействия ![]() 0,47; для стратегии сотрудничества
0,47; для стратегии сотрудничества ![]() 0,55. Итак, согласно критерию математического ожидания наиболее подходящий тип стратегии взаимодействия вуза с клиентами – стратегия защиты. Фактически математическое ожидание отражает среднее значение целесообразности применения стратегии. Однако данный показатель вряд ли можно назвать характеристикой качества выбранного типа стратегии. Дело в том, что при подсчете среднего значения целесообразности применения стратегии наблюдается эффект компенсации «плохих» показателей «хорошими». Например, для стратегии защиты среднее значение целесообразности применения составляет 0,6, однако во втором сценарии, вероятность которого равна 0,23, целесообразность применения значительно ниже среднего значения. При этом компенсация этого «плохого» показателя произошла за счет «хороших» показателей – целесообразностей применения типа стратегии в остальных пяти сценариях. Однако в реальности такая компенсация не происходит. В случае наступления второго сценария с «плохим» показателем стратегия защиты может оказаться не подходящей и привести к ухудшению отношений вуза с группой стейкхолдеров, а в крайнем случае к разрыву отношений.
0,55. Итак, согласно критерию математического ожидания наиболее подходящий тип стратегии взаимодействия вуза с клиентами – стратегия защиты. Фактически математическое ожидание отражает среднее значение целесообразности применения стратегии. Однако данный показатель вряд ли можно назвать характеристикой качества выбранного типа стратегии. Дело в том, что при подсчете среднего значения целесообразности применения стратегии наблюдается эффект компенсации «плохих» показателей «хорошими». Например, для стратегии защиты среднее значение целесообразности применения составляет 0,6, однако во втором сценарии, вероятность которого равна 0,23, целесообразность применения значительно ниже среднего значения. При этом компенсация этого «плохого» показателя произошла за счет «хороших» показателей – целесообразностей применения типа стратегии в остальных пяти сценариях. Однако в реальности такая компенсация не происходит. В случае наступления второго сценария с «плохим» показателем стратегия защиты может оказаться не подходящей и привести к ухудшению отношений вуза с группой стейкхолдеров, а в крайнем случае к разрыву отношений.
Допустим, пороговое значение целесообразности применения стратегии составляет 0,5, тогда, чтобы оценить детерминированный эквивалент (ДЭ) типов стратегий, перейдем к новой переменной ![]() . Величина
. Величина ![]() указывает в каждом конкретном случае насколько этот случай улучшает пороговое значение целесообразности применения стратегии (если
указывает в каждом конкретном случае насколько этот случай улучшает пороговое значение целесообразности применения стратегии (если ![]() ) или насколько он ухудшает его (если
) или насколько он ухудшает его (если ![]() ).
).
Составим таблицу пересчета переменной ![]() (таблица 2) и перейдем от случайных величин
(таблица 2) и перейдем от случайных величин ![]() ,
, ![]() ,
, ![]() ,
, ![]() к случайным величинам
к случайным величинам ![]() ;
; ![]() ;
; ![]() ;
; ![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Далее ЛПР должно указать ДЭ типов стратегий на интервале [-0,14; 0,23]. Для этого вначале построим кривую эквивалентов типов стратегий взаимодействия, где значения переменной ![]() заключены между -0,14 и 0,23 (между наихудшим и наилучшим значениями переменной
заключены между -0,14 и 0,23 (между наихудшим и наилучшим значениями переменной ![]() ).
).
Таблица 2 – Пересчет переменной ![]()
|
|
0,36 |
0,4 |
0,43 |
0,44 |
0,45 |
0,46 |
0,47 |
0,5 |
0,54 |
0,55 |
|
|
-0,14 |
-0,1 |
-0,07 |
-0,06 |
-0,05 |
-0,04 |
-0,03 |
0 |
0,04 |
0,05 |
|
|
0,56 |
0,57 |
0,6 |
0,61 |
0,62 |
0,63 |
0,67 |
0,71 |
0,72 |
0,73 |
|
|
0,06 |
0,07 |
0,1 |
0,11 |
0,12 |
0,13 |
0,17 |
0,21 |
0,22 |
0,23 |
Чтобы построить данную кривую, необходимо найти пять точек ![]() , причем последние три – путем опроса ЛПР. Заметим также, что здесь
, причем последние три – путем опроса ЛПР. Заметим также, что здесь ![]() – наихудшее значение переменной
– наихудшее значение переменной ![]() ;
; ![]() – наилучшее значение переменной
– наилучшее значение переменной ![]() ;
; ![]() <
<![]() <
<![]() .
.
Опрос ЛПР происходит в следующей форме. Например, для нахождения точки (![]() ;0,5) ЛПР задается вопрос: «Какое должно быть значение целесообразности применения типа стратегии взаимодействия
;0,5) ЛПР задается вопрос: «Какое должно быть значение целесообразности применения типа стратегии взаимодействия ![]() при уровне полезности, равной 0,5?». Аналогичным образом задаются вопросы для нахождения точек (
при уровне полезности, равной 0,5?». Аналогичным образом задаются вопросы для нахождения точек (![]() ;0,25) и (
;0,25) и (![]() ;0,75).
;0,75).
С учетом нежелательности ухудшения порогового значения целесообразности применения стратегии (т.е. нежелательности отрицательных значений переменной ![]() ) зададим ДЭ типов стратегий при значениях параметра p=0,5; 0,25; 0,75 следующим образом:
) зададим ДЭ типов стратегий при значениях параметра p=0,5; 0,25; 0,75 следующим образом:
![]() ,
, ![]() ,
, ![]() .
.
Теперь строим кривую эквивалентов по пяти точкам (рис. 1).
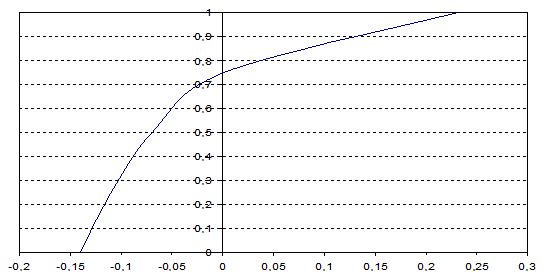
Рисунок 1 – Эмпирическая кривая эквивалентов
Далее, используя алгоритм нахождения детерминированного эквивалента типов стратегий взаимодействия, определим ожидаемые полезности стратегий ![]() ,
, ![]() ,
, ![]() ,
, ![]() :
:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Таким образом, по критерию ожидаемой полезности наиболее подходящий тип стратегии взаимодействия – стратегия удовлетворения запросов. Стратегия защиты также имеет высокий показатель ожидаемой полезности. При этом при выборе типа стратегии взаимодействия с группой заинтересованных сторон должна учитываться степень развитости соответствующих компетенций вуза (наличие ключевых компетенций), необходимых для реализации каждого из возможных типов стратегий [6]. Однако в любом случае окончательный выбор остается за ЛПР.
Рецензенты:
Ембулаев В.Н., д.э.н., д-р транспорта, доцент, ФГБОУ «Владивостокский государственный университет экономики и сервиса», г. Владивосток.
Мазелис Л.С., д.э.н., директор института информатики, инноваций и бизнес-систем, заведующий кафедрой математики и моделирования, ФГБОУ «Владивостокский государственный университет экономики и сервиса», г. Владивосток.



