Решая проблему обучения в вузе, следует заметить, что качество овладения знаниями во многом зависит не только от характера обучения в нем, но и от школьной подготовки студентов, которая, в свою очередь, чаще всего является недостаточной. Это находит свое подтверждение в результатах единого государственного экзамена по математике и тестового входного контроля, ежегодно проводимого курирующими кафедрами в начале учебного года на первых курсах всех специальностей. В частности, анализ вступительных тестов показывает, что около 50% абитуриентов в последние годы получают оценку «неудовлетворительно», из них почти 76% хотя и знакомы с основными математическими понятиями, но путаются в расчетах, вычислениях, допускают грубые ошибки в применении математического аппарата, показывают незнание основных формул элементарной математики; 24% фактически не владеют математическими знаниями и навыками за курс средней школы. В условиях возможности получения образования по договору многие из таких абитуриентов оказываются студентами-первокурсниками.
Это приводит к тому, что большинство студентов, начинающих учиться в вузе, не подготовлены к осуществлению сколько-нибудь продуктивной учебной деятельности (состояние выученной беспомощности). Им трудно даются поиск нетривиальных решений, анализ непривычного материала, самостоятельное формулирование выводов, оперирование математической символикой, умение устанавливать генетические связи и причинно-следственные отношения, выстраивание в логический ряд совокупности умозаключений. Основная причина такого положения видится в том, что предъявляемая информация еще в школе преподносится вне имеющейся системы знаний, случайным образом накапливаясь в их когнитивно-идентификационном фонде лишь только алгоритмично сдать ЕГЭ. В качестве дополнительных факторов, негативно влияющих на качество фундаментальной подготовки студентов, можно указать постоянно увеличивающийся дефицит учебного времени; существенное усиление роли самостоятельной работы при недостаточном развитии у студентов соответствующих умений самообучения и саморазвития.
На наш взгляд, для решения данной проблемы нужно многое поменять в методике подготовки к сдаче выпускных экзаменов, а также пересмотреть сам тестовый вариант ЕГЭ с учетом дальнейшего обучения в вузе.
Анализируя школьный образовательный стандарт как основную математическую базу для обучения в вузе, хотелось бы остановиться на следующем. Конечно, он содержит много важных для дальнейшего изучения математики тем, но, к сожалению, не все они рассматриваются учителями в должной мере. Например, изучая комплексные числа в университете, студенты воспринимают ее как новую и ранее не известную тему, хотя образовательный стандарт школы ее учитывает. Раздел теории вероятности в школе ограничен лишь простейшими задачами на классическое определение вероятности. Не уделяется внимания элементам комбинаторики, хотя их изучение прописано в стандарте и не менее важно как при изучении данного раздела в вузе, так и при сдаче ЕГЭ. Студенты впервые сталкиваются с понятием координатного метода решения геометрических задач, который также важен для изучения аналитической геометрии в вузе. Решение задач С2 в ЕГЭ также чаще проще решаются с использованием данного метода и вызывают трудности в его незнании.
Для того чтобы обучение математике в вузе было более успешно, особое внимание следует уделить следующим темам. Преобразованию выражений: алгебраических, тригонометрических, логарифмических; понятию первообразной и интеграла; координатному методу решения геометрических задач; знакомству с комплексными числами; элементам комбинаторики. На наш взгляд, более плотное изучение данных тем значительно облегчило обучение студентов.
В связи с вышесказанным выделим некоторые рекомендации для учителя математики:
- Материал на уроках необходимо излагать в простой, доступной, понятной большинству учащихся, форме.
- Формы работы на уроках необходимо разнообразить, повышая тем самым интерес к предмету.
- Необходимо добиваться от учащихся не формального усвоения программного материала, а глубокого осознанного его понимания.
- В процессе преподавания необходимо делать определенные акценты на те разделы, которые представлены в тестах ЕГЭ.
- Объяснение нового материала необходимо строить как можно более наглядно, создавать яркие образы и конкретные представления об изучаемом материале, чтобы в наибольшей степени воздействовать на чувства ученика, вызвать у него наглядно-образное мышление.
- Необходимо разработать систему контроля знаний учеников и возможность устранения пробелов в их знаниях.
- Необходимо сформировать у всех учащихся достаточно высокий уровень учебной самодеятельности, которая явилась бы для них формой самоосуществления, формой свободной, творческой деятельности.
Рассматривая нашу проблематику дальнейшего обучения математике в вузе, чтобы она была более эффективной и успешной, учителю при отработке умений и навыков решения заданий ЕГЭ следует обращать особое внимание на следующие математические тематики:
- задания, связанные с нахождением области значения функции (периодичности, четности, нечетности);
- нахождение области допустимых значений неизвестного (ненахождение которого ведет к появлению в ответе постороннего корня);
- умножение и деление уравнения на выражение, содержащее неизвестную величину или параметр (необходимо отдельно исследовать случай, когда это выражение равно нулю);
- графический способ решения уравнений и неравенств;
- отработку свойств графиков функции, которые будут необходимы не только для чтения графиков, но и для решения комбинированных уравнений;
- графики производных функций;
- задания, связанные с расширением понятия степени (с натуральным, нулевым показателем, степень с целым отрицательным показателем);
- решение текстовых и геометрических задач на каждом уроке;
- графическому изображению геометрических фигур и тел;
- постановку вопроса теста («найти сумму корней; найти удвоенное произведение корней; найти наибольший корень и т.д.»);
- вычислительные навыки;
- преобразование тригонометрических выражений и уравнений, где формулы приведения заданы неявно;
- вычислению производной, ее геометрическому смыслу и применению;
- вычислению первообразных.
Если учесть все наши рекомендации, анализ школьной и вузовских программ, то тестовый вариант, содержащий школьный материал, необходимый для вузовского обучения математике, должен представлять собой следующее.
Тест
Упростите выражение: 
А) 
Б) 
В) 
Упростите выражение: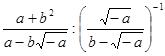 
А) 1 Б) 
В) a-b
Упростите выражение: 
Найти значение выражения: 
А) 2 Б) 8 В) -2
Сопряженным для комплексного числа 
будет 
:
А) 
Б) 
В) 
Найти значение выражения: (3i-2)(2+4i)-i
А) -16-3i Б) 6+3i В) -4-7i
Упростите выражение: 
А) 
Б) 
В) 
Первообразной для функции 
будет:
А) 
Б) 
В) 
Вычислить площадь фигуры, ограниченную заданными линиями: 
.
А) 30 Б) 4,5 В) 1,5
Вычислить 
А) 
Б) 
В) 
Найти скалярное произведение векторов a и b, если 
В треугольнике ABC AC=BC, AB=30, cosA=5/13. Найдите высоту CH.
А) 36 Б) 12 В) 78
В правильной пирамиде PABCD т.K середина бокового ребра PC. Найти расстояние от вершины P до плоскости BDK, если известно, что сторона основания пирамиды равна 6√2, а высота равна 8.
А) 5 Б) 3,2 В) 4,8
Прямая, проходящая через т.А(2;2), касается графика функции y=f(x) в точке В(-3;5). Найти значение производной функции f(x) в точке с абсциссой х=-3.
А) -0,6 Б) 0,6 В) 1
Найти производную 
А) 
Б) 
В) 
Сколькими способами можно отобрать команду из 7 человек из 20 спортсменов?
А) 77520 Б) 120 В) 54987
Найти вероятность того, что при первых трех подбрасываний монеты выпадет орел.
Найти наибольшее значение функции 
на 
.
А) 
Б) 4 В) 8
Объем конуса равен 86, через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
А) 3,5 Б) 10,75 В) 8,25
Решить систему неравенств: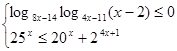 
А)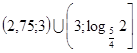 
Б)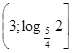 
В) нет решений.
Именно такой вариант итоговой работы школьного курса по математике отвечает всем требованиям для успешного продолжения ее обучения в вузе.
Рецензенты:
Родионов М.А., д.п.н., профессор, зав. кафедрой «Алгебра и теория и методика обучения и воспитания математике и информатике», ФГБОУ ВПО «Пензенский государственный университет», г. Пенза.
Садовников Н.В., д.п.н., профессор, профессор кафедры «Компьютерные технологии», ФГБОУ ВПО «Пензенский государственный университет», г. Пенза.