Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Введение

Многие научно-технические задачи описываются с использованием аппарата дифференциальных уравнений. При этом аналитическое решение задачи неизвестно или его не удается выразить в элементарных функциях. Научным сообществом проведено множество исследований, посвященных разработке методов, с помощью которых можно получить приближенное решение дифференциальных уравнений и систем. Особого внимания заслуживают исследования, направленные на разработку численных методов интегрирования жестких систем обыкновенных дифференциальных уравнений (ОДУ), а также систем, полученных в результате дискретизации уравнений в частных производных [1, 6, 8]. Жесткие задачи очень распространены во многих областях прикладных исследований: управление, биология, химико-технологические процессы, электротехника, динамика жидкостей, акустика, пластическая деформация и т.д.

Данное исследование посвящено развитию одношаговых многоточечных блочных методов. Предлагаемый метод является самостартующим и может быть применен для численного решения задачи Коши для уравнений и систем ОДУ первого порядка. Для создания блочных методов необходимо решить задачи: 1) определить коэффициенты уравнений для блоков, включающих k точек; 2) провести проверку коэффициентов метода на согласованность; 3) определить порядок точности (аппроксимации) и область устойчивости метода; 4) установить сходимость метода; 5) провести численные эксперименты.

Теоретический обзор

Для численного решения уравнений и жестких систем ОДУ можно использовать различные методы: формулы дифференцирования назад (ФДН или методы Гира) [4, 7, 8, 10], методы Розенброка, неявные методы типа Рунге-Кутты [2, 3], а также явные разностные схемы [1]. Данные методы устойчивы, шаг интегрирования можно выбирать произвольно, руководствуясь требованиями точности, а не устойчивости. Классические неявные многошаговые методы не являются самостартующими и для их использования требуется «участок разгона». В свою очередь явные методы являются менее трудоемкими при их реализации, но им свойственны определенные недостатки, в частности, условная устойчивость, что существенно ограничивает область их применения.

Блочным будем называть метод, с помощью которого в блоке из k равноотстоящих расчетных точек xn+1, ..., xn+i,…, xn+k вычисляются одновременно новые k значений функции yn+1, ..., yn+i,…, yn+k. Будем называть блочный метод одношаговым, если для расчета значений в новом блоке используется только последняя точка предшествующего блока. Если используются несколько точек предшествующего блока, то будем говорить о многошаговых блочных методах. Впервые идеи создания блочных методов решения уравнений и систем ОДУ были предложены в 1953 году У. Милном. Дальнейшее развитие этих идей принадлежат Дж. Россеру, который предложил оригинальные идеи использования методов Рунге-Кутты. Развитие линейных многошаговых методов для нахождения приближенного решения уравнений и систем ОДУ могут быть получены с использованием различных подходов: метод коллокаций, метод интерполяции степенных рядов, разложение в ряд Тейлора [7, 9, 10].

Коэффициенты блочного метода

Запишем задачу Коши для ОДУ первого порядка в виде

y’=f(x, y), (1)

где 0 < x ≤ b и задано начальное условие y(0) = y0. Для записи n-шагового k-точечного блочного метода в виде ФДН будем использовать: вычисленные значения искомой функции Ym=(yn+1, ..., yn+i, …, yn+k)T, Ym-1=(yn−k+1, yn−k+2, ..., yn)T и производные Fm=(fn+1, ..., fn+i, …, fn+k)T в блоке равноотстоящих расчетных точек xn+1, ..., xn+i,…, xn+k. Здесь m = 1, 2, … номер текущего блока, k – количество точек в блоке, n + i = k∙(m – 1) + i – номер текущей точки в блоке, xn+1 – начало блока, xn+i, i = 2, 3, …, k – 1 – точки внутри блока, xn+k – конец блока. Обозначим через h =xn+i – xn+i–1 размер шага интегрирования, тогда размер блока равен (k –1)∙h. В общем случае n-шаговый k-точечный блочный метод можно записать [5]:

. (2)

Здесь k×k матрицы коэффициентов A(i) и B(i), i = 0, 1, …, n, явный вид которых необходимо определить. Применение формулы (2) генерирует новый блок, включающий k новых значений Ym = (yn+1, ..., yn+i, …, yn+k)T в блоке из k равноотстоящих точек.

Мы предлагаем использовать метод коллокаций для построения одношагового девятиточечного (k = 9) блочного метода в виде ФДН. Предположим, что точное решение у(х) локально представлено на интервале [x0, x0 + k·h] непрерывным решением Y(х) вида

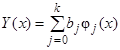, (3)

где bj – неизвестные коэффициенты, которые необходимо определить и φj(x) – некоторые полиномы степени j=0, 1, ... , k. Мы предлагаем конструировать одношаговый девятиточечный блочный метод в виде ФДН, выбирая φj(x) = xj и используя следующие коллокационные соотношения

Y(xn+j) = yn+j, j = 0, 1, ..., k – 1 и , (4)

где yn+j является приближением для точного решения y(xn+j), fn+k = f(xn+k, yn+k). Использование соотношений (4) приводит к системе линейных алгебраических уравнений, которую необходимо решить для получения коэффициентов bj, j=0, 1, ... , k. Далее полученные коэффициенты bj, j=0, 1, ... , k подставляются в выражение (3) и после некоторых алгебраических вычислений при k = 9 получаем следующее выражение для Y(х):

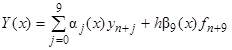, (5)

где αj(x)и β9(x) – коэффициенты метода. Далее формула(5) используется для записи первого уравнения одношагового девятиточечного метода в виде ФДН:

yn+9 = (280yn – 2835yn+1 + 12960yn+2 – 35280yn+3 + 63504yn+4 – 79380yn+5 +
+ 70560yn+6 – 45360yn+7 + 22680yn+8 + 2520∙h∙fn+9)/7129. (6)

Для записи остальных восьми выражений конструируемого метода воспользуемся опять выражением (5), применив к нему операцию дифференцирования в точках x=xn+j, j=1, 2, …, 8 соответственно. При этом будем использовать следующее выражение дифференциального исчисления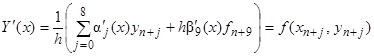.Приведем в явном виде остальные коэффициенты одношагового девятиточечного метода в форме ФДН:

fn+1 = (–796yn– 427253yn+1/35 + 28336yn+2 – 98336yn+3/3 + 97160yn+4/3–23849yn+5–

–23849yn+5 + 184912yn+6/15 – 12368yn+7/3 + 4924yn+8/7 – 35∙h∙fn+9)/(7129h), (7)

fn+2 = (801yn/8 – 3587yn+1/2 – 154791yn+2/20 + 49483yn+3/3 – 48895yn+4/4 +
+48013yn+5/6 – 46543yn+6/12 + 6229yn+7/5 – 4969yn+8/24 + 10∙h∙fn+9)/(7129h),

fn+3 = ( –2423yn/84 + 10851yn+1/28 – 3081yn+2 – 259573yn+3/60 + 21135yn+4/2 –
–20757yn+5/4 + 6709yn+6/3 – 18867yn+7/28 + 15087yn+8/140 – 5∙h∙fn+9)/(7129h),

fn+4 = (817yn/56 – 3659yn+1/21 + 1039yn+2 – 14426yn+3/3 – 1325yn+4 + 7003yn+5 –
–6793yn+6/3 +12746yn+7/21 – 5113yn+8/56 + 4∙h∙fn+9)/(7129h),

fn+5 = ( –831yn/70 + 1861yn+1/14 – 2114yn+2/3 + 7339yn+3/3 – 7255yn+4 +
+15833y5/10 + 13838y6/3 – 6499y7/7 + 5239y8/42 – 5∙h∙fn+9)/(7129h),

fn+6 = (2563yn/168 – 11481yn+1/70 + 3261yn+2/4 – 7549yn+3/3 + 22395yn+4/4 –
–22017yn+5/2 +280573yn+6/60 +20127yn+7/7 – 16347yn+8/56 + 10∙h∙fn+9)/(7129h),

fn+7 = ( –901y n/28 + 4037yn+1/12 – 8029yn+2/5 + 55783yn+3/12 – 55195yn+4/6 –
–54313yn+5/4 –52843yn+6/3 +1178937yn+7/140 + 5869yn+8/4 – 35∙h∙fn+9)/(7129h),

fn+8 = (1041y n/8 – 9334yn+1/7 + 18578yn+2/3 – 258412yn+3/15 + 64015yn+4/2 –
–126266yn+5/3 +123326yn+6/3–33556yn+7+4134649yn+8/280 + 280hfn+9)/(7129h).

Система (6)-(7) определяют одношаговый девятиточечный метод в виде системы ФДН. Вычислительная сложность метода коллокаций (3)-(5) для нахождения коэффициентов метода определена сложностью нахождения обратной матрицы и имеет кубический порядок O(k3), зависит от размера входа (в нашем случае это количество точек в блоке k). Исследование роста сложности при увеличении размера входа с k = 2 до k = 9, свидетельствуют, что асимптотически сложность не изменяется с ростом порядка блочного метода.

Согласованность коэффициентов и порядок точности

Для проверки согласованности коэффициентов блочного метода (6)-(7) воспользуемся подходом, предложенным в монографии [5]. Для этого вычислим константы погрешности многошаговых методов Сp+1 и сравним их с нулем:

для p=0, 1,…, 8 и C10≠0. (8)

Выполнение условий (8) позволяет установить порядок аппроксимации. Последовательно подставив в выражение (8) коэффициенты ai и bi, i=1, 2,…, 9 из выражения (6) и варьируя p, можно показать, что Сp+1 = 0, p=0, 1, 2,…, 8, но при этом С10 = −252/7129. В этом случае можно заметить, что выражение (6) определяет метод девятого порядка точности. Аналогичные вычисления можно провести для системы (7). При этом Сp+1=0, p=0, 1, …, 8 для всех уравнений из системы (7) и С10=(3722/320805, −7489/2566440, 7549/5988360, −7633/8982540, 7759/8982540, −7969/5988360, 8389/2566440, −9649/641610) соответственно.

Область устойчивости и сходимость

В качестве основы определения области устойчивости блочных методов будем использовать метод характеристического полинома [5]. Для этого рассмотрим задачу

y'= ly, . (9)

Запишем выражение (2) для одношагового (n = 1) блочного метода:

, (10)

явный вид k×k матриц коэффициентов A(1), B(0) и B(1) определен в системе (6)-(7). Применим выражение (10) к тестовой задаче (9), будем иметь

Ym+1=(I – z B)-1A Ym, (11)

где , zC, I – единичная матрица. Явный вид k×k матриц A, В может быть получен нормализацией A(1), B(0) и B(1), определенных в (6)-(7). Доминирующее собственное значение матрицы (I – z B)-1A будет определять рациональную функцию R(z), определяющую область устойчивости метода (6)-(7) на комплексной плоскости

R(z)=R1(z)/R2(z), (12)

здесь R1(z) = 15120 – 60480z + 114660z2 + 136080z3 + 112245z4 + 6728z5 + 2953z6 + 9132z7 + 1680z8, R2(z) = 15120 – 75600z + 182700z2 – 283500z3 + 316365z4 – 269325z5 + 180920z6 –97725z7 + 42774z8 – 15120z9.

На рис. 1 приведен график области устойчивости и полюсы функции устойчивости предложенного девятиточечного метода (6)-(7) в сравнении с областью устойчивости восьмиточечного блочного метода [4], ближайшего по точности.

Области устойчивостей указанных методов лежат вне границ кривой S = ={R(z) ≤ 1: zC} [4]. Области устойчивости методов практически совпадают, при этом предложенный метод (6)-(7) имеет более высокий порядок аппроксимации. Для функции устойчивости (12) определены полюсы с координатами (0.767, 0.000), (–0.454, ±1.463), (0.219, ±1.047), (0.549, ±0.686) и (0.716, ±0.341) соответственно. Наличие указанных полюсов накладывает ограничение на область устойчивости метода, при этом предлагаемый метод (6)-(7) является А(α)-стабильным, где α=72.760 (рис. 1). Блочный метод (2) обладает нуль-устойчивостью, если корни его характеристического полинома

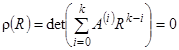(13)

лежат внутри единичной окружности |Rj| ≤ 1, а корни, принадлежащие единичной окружности |Rj| = 1 – простые, j=1, 2, …, k [5]. Рассмотрим блочный метод (11) при h→0, в этом случае будем иметь и характеристический полином (13):

ρ(R) = det(R∙I– A(1)) =2520∙R8(1 – R)/7129 = 0.

Таким образом, выполнение условий согласованности коэффициентов (9) и нуль-устойчивости (13) позволяет сделать вывод, что метод (11) является сходящимся.

Результаты численных расчетов

Для проведения тестирования предложенного блочного метода (6)-(7) разработан алгоритм численного решения уравнений и систем ОДУ. Данный алгоритм программно реализован в системе MatLAB. Кратко приведем полученные результаты численного эксперимента (табл. 1-2) на задачах различной степени жесткости, имеющих аналитические решения [4, 9, 10]. Для сравнения точности полученных численных решений использована характеристика [4] , которую будем называть максимальной абсолютной погрешность численного решения. Данная погрешность выбирается среди погрешностей для всех расчетных точек интервала интегрирования.

Задача1. Автономное линейное ОДУ: y'= –9y, y(0)=e. Аналитическое решение у=e1-9x.

Задача 2. Автономное нелинейное ОДУ: y'=50/y–50y, y(0)=.

Аналитическое решение y=(1+e–100x)1/2.

Таблица 1

Задача 3. Жесткая автономная система нелинейных ОДУ

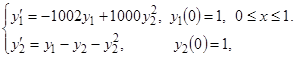
Аналитическое решение y1=e–2x, y2=e–x.

Задача 4. Жесткая система нелинейных неоднородных ОДУ

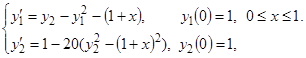
Аналитическое решение y1=1/(1+х), y2=1+х.

Таблица 2

Из результатов расчетов (табл. 1-2) следует, что с помощью предлагаемого одношагового девятиточечного блочного метода (6)-(7) при величине шага h=10-6…10-2 можно получить численное решение тестовых задач 1-4 с более низкой погрешностью MaxE по сравнению с существующими методами.

Заключение

В работе использован коллокационный подход для получения формул линейных неявных n-шаговых k-точечных блочных методов. На примере одношагового девятиточечного метода в виде формул дифференцирования назад определены коэффициенты блочного метода, проведена их проверка на согласованность, определен порядок аппроксимации, установлена сходимость и область устойчивости предложенного метода. Предложенный блочный метод определяет метод девятого порядка точности, является А(α)-стабильным, α=72.760. Вычисление приближенного значения искомой функции в каждой k-ой точке внутри блока независимо друг от друга и может рассматриваться как отдельная (параллельная) задача. Данные методы можно использовать для решения уравнений и систем ОДУ, в том числе жестких систем.

Работа выполнена при поддержке гранта РФФИ по проекту № 13-01-90903 мол_ин_нр, государственного задания «Наука» № 1.604.2011 (Россия).

Рецензенты:

Шумилов Б.М., д.ф.-м.н., профессор кафедры прикладной математики, ГОУ ВПО Томский государственный архитектурно-строительный университет, г. Томск.

Гришин А.М., д.ф.-м.н., профессор, зав. кафедры физической и вычислительной механики. ФГБОУ ВПО НИ Томский государственный университет, г. Томск.