Введение
В вопросах территориального планирования и природопользования одной из ведущей технологией, сочетающей возможности традиционной картографии и интеллектуальной обработки данных, является геоинформационная система (ГИС). Наиболее значимая составляющая функциональности ГИС в аналитических задачах заключается в использовании моделей реальных явлений. Характерной чертой этих моделей является комбинирование и преобразование исходных данных в соответствии с алгоритмом решения и последующая интерпретация полученных результатов в виде карты местности. В то же время, для достижения результатов, способных удовлетворить запросы пользователей, нередко приходится сталкиваться с несовершенством применяемых подходов и, как следствие, с недостаточной адекватностью формируемых на их базе выводов. В связи с этим, наиболее эффективными являются нечеткие методы моделирования, базирующиеся на аппарате нечеткой логики (fuzzy logic), с помощью которых, полагаясь на знания экспертов, могут быть получены позитивные результаты в итерационном процессе уточнения непротиворечивой модели. Такие модели способны учесть неточность (нечеткость) в условиях, свойственных задаче, и обеспечить достижение приемлемого решения.
Использование методов нечеткой логики в ГИС является более продвинутым, приближенным к естественным человеческим суждениям подходом как для традиционных задач, так и тех задач, для которых до недавнего времени решения не были вполне пригодными для использования [4-6]. Само решение задачи может состоять в наложении тематических пространственных данных, например, при выборе подходящих по заданным критериям территорий, и применения моделей пригодности.
Постановка задачи
В ГИС изучение территории зачастую основывается на поиске определенных закономерностей во взаимном расположении пространственных объектов. Анализируя такой параметр как расстояние, эксперт как правило характеризует его как "далеко", "близко" и др., в соответствии с чем и описывает необходимое условие для поиска определенного местоположения. Постановка задачи состоит в формализации описания суждений экспертов в терминах нечеткой логики совместно с описанием пространственного взаиморасположения объектов на карте. В последующем решение задачи выполняется на основе методов, применяемых к нечетким множествам, результаты которой проходят процедуру дефаззификации и визуализации их на карте как более удобного и понятного способа предоставления вывода пространственного анализа [1].
Тем не менее, существует целый ряд задач, в рамках решения которых лежит изучение поверхности территории в целом, т.е. требуется анализ всего множества точек, из которых состоит непрерывная поверхность. В таком случае, устанавливается пространственное взаимоотношение географических объектов непосредственно с каждой точкой местности, результат вычисления которых будет представлен в виде новой поверхности, отражающей участки в той или иной степени удовлетворяющие заданным условиям задачи.
Рассмотрим векторную карту местности K (рис. 1), описывающую пространственное расположение множества объектов O, принадлежащих одному из n типов и сгруппированных в соответствии с типами в слои 
, 
:
,
.
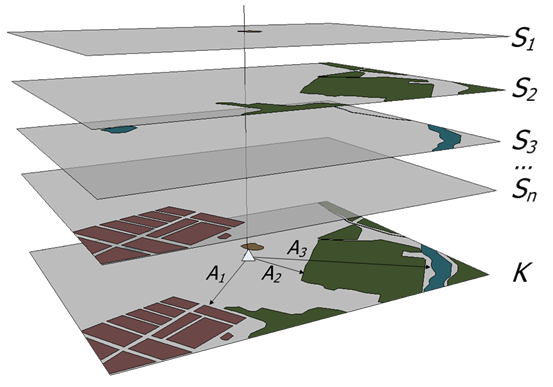
Рис. 1 –– Карта, состоящая из векторных слоев {Si}
Пространственные характеристики объектов на плоскости, описываемых картой заданного фиксированного масштаба M, охарактеризуем следующим образом:
- точечные объекты (колодцы, посты гидрологического контроля и др.) – парой координат:
;
- линейные объекты (реки, авто- и ж/д дороги и др.) – упорядоченным набором из r пар координат:
;
- полигональные объекты (населенные пункты, озера, лесные массивы и др.) – упорядоченным набором из r пар координат, причем координаты начальной точки совпадают с координатами конечной точки:
.
Как было отмечено, одной из основных количественных характеристик положения объектов является расстояние от одного объекта до другого. В случае с анализом поверхности это расстояние от точки пространства Р до объекта Оi (рис. 2).
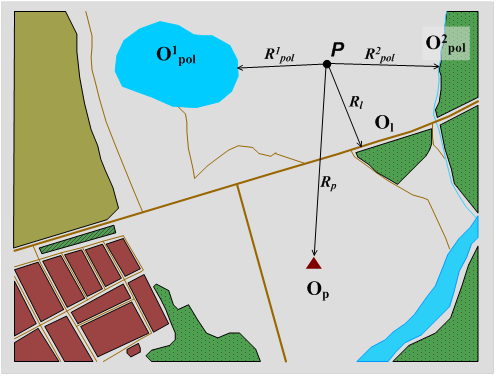
Рис. 2 – Взаиморасположение объектов на карте
Если рассматриваются точечные объекты, расстояние определяется согласно евклидовой метрике:
. (1)
При оценке расстояния от линейного объекта до точки, необходимо оперировать понятием кратчайшего расстояния, определяемого как:
. (2)
Аналогичным образом определяется расстояние между точкой и объектом полигонального типа:
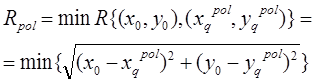(3)
Определив расстояния для каждой точки пространства и обозначив набор расстояний от одной точки до всех объектов на карте как 
, приступим к определению условий задачи, которые в качестве параметров будут использовать расстояния между различными группами объектов.
Допустим, необходимо выбрать местоположение для объектов Oиск, на которое оказывают влияние факторы 
, характеризующие расстояние ri от объектов Оi до искомого положения объекта Оиск.
Каждый фактор AiIn в рамках нечеткой логики будет называться лингвистической переменной, которая определяется некоторым набором термов:
.
Для факторов расстояний в качестве термов могут выступать следующие лингвистические значения «близко», «недалеко», «далеко». Степень отношения значений ri к определенному терму лингвистической переменной выражается функцией принадлежности 
, где 
– область определения входных переменных ri (рис. 3) [2-3].
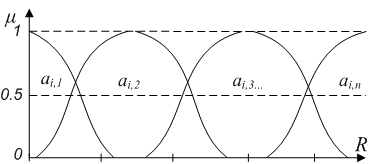
Рис. 3 – График функции принадлежности для входной лингвистической переменной АInp
В зависимости от выбора задачи, пригодность местоположения объекта Оиск характеризуется лингвистической переменной AOut. Задачей нечеткого вывода является определение числового значения для выходной переменной AOut, согласно условиям задачи AIn:
. (2.4)
Соответственно, каждой выходной переменной присуще свои значения термов, характеризующие степень пригодности искомого участка как «не пригодно», «не достаточно пригодно», «пригодно» и т.д.:
Областью определения в этом случае будет выступать m-бальная шкала, которая обозначает степень пригодности местоположения 
[3]. Функции принадлежности 
, где 
для нечетких множеств {dj} представлены d2 на рисунке 4.
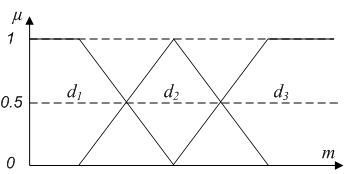
Рис. 4 – График функции принадлежности для выходной лингвистической переменной AOut
После определения входных и выходных значений, необходимо установить между ними зависимость, т.е. сформировать базу правил систем нечеткого вывода.
В качестве правил логического вывода будем использовать операцию нечеткого И (минимум), с помощью которой принадлежность выводу «отсекается» по высоте, соответствующей степени истинности предпосылки правила. Далее нечеткие подмножества, назначенные для каждой выходной переменной, объединяются для формирования единого нечеткого подмножества для каждой переменной:
ЕСЛИ 
И 
И…И 
ИЛИ 
И 
И…И 
……..
ИЛИ 
И 
И…И 
ТО 
,
где 
– нечеткий терм, которым оценивается значение входа 
в строчке с номером jp (
), kj – количество строчек-коньюкций, в которых выход y оценивается нечетким термом dj, z – количество термов, используемых для лингвистической оценки выходных данных.
Таким образом, приведенная выше система логических высказываний записывается с помощью операций объединения 
и пересечения 
:
(5)
Нечеткая база знаний вида (5) является базой знаний Мамдани с MISO-структурой (Multiple Input – Single Output) [1-3].
Теперь полученные результаты нечеткого вывода следует преобразовать в обычные количественные значения, чтобы оценить степень удовлетворенности каждой точки пространства местоположению согласно условиям задачи. В данной задаче рассматривается деффазификация по методу центра тяжести:
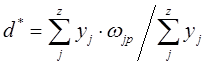(6)
Физическим аналогом этой формулы является нахождение центра тяжести плоской фигуры, ограниченной осями координат и графиком функции принадлежности нечеткого множества.
Подобным образом, вычислив значения d* для всего множества точек пространства получим новую поверхность, отображающую желательные и нежелательные участки для установления объектов Oиск в соответствии с мнениями экспертов.
На рисунке 5 представлены территории пригодности местоположения санитарно-защитной зоны полигона отходов (СЗЗ) (5а) и мусороперегрузочных станций (МПС) (5б), , полученных в результате описанного выше анализа. Для решения приведенных примеров задач в основном учитывался такой фактор как взаиморасположение объектов на карте, участвующих в сфере обращения с отходами и влияющих на пригодность территории для установки СЗЗ и МПС.
Заключительная часть
Разработаны способ формализации нечетких суждений о взаимном расположении географических объектов для представления сложных пространственных моделей и система получения на их базе результатов методами нечеткого логического вывода. Этот метод благодаря свободе и многообразию рассуждений о поставленной задаче, повышает гибкость и выразительность анализа и интерпретации данных, и потому может служить основой для проведения интеллектуального анализа географических данных
а)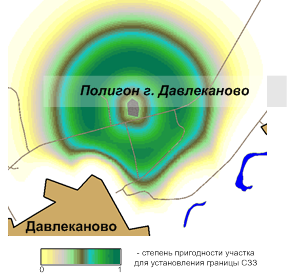 
б)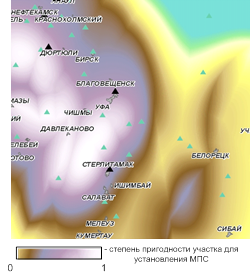
Рис. 5 – Результат нечеткого вывода на карте
Рецензенты:
Куликов Г.Г., д.т.н, профессор, зав. кафедрой АСУ, ФГБОУ ВПО УГАТУ, г.Уфа.
Христодуло О.И., д.т.н., доцент, зав.кафедрой ГИС, ФГБОУ ВПО УГАТУ, г.Уфа.