Введение
Моральное старение сложных многокомпонентных электронных систем с блочно-модульной структурой оборудования, к каким относятся технологические подсистемы и элементы большинства прикладных распределенных информационных систем (ПРИС), может проявляться в нескольких формах [1]. Во-первых, это экономическая форма морального старения (моральное старение первого рода) – как следствие появления на рынке новых образцов техники, не уступающих по эффективности, но более дешевых для потребителя, что делает производство устаревшей техники нерентабельным вследствие снижения спроса на нее. Во-вторых, это технологическая форма морального старения – отставание функциональных возможностей ПРИС от изменяющихся потребностей надсистемы-потребителя информации, как по составу функций ПРИС, так и по качеству их выполнения (моральное старение второго рода). Перечисленные формы морального старения достаточно широко описываются в современной литературе, см., например [4, 6, 7].
Однако существует еще одна форма морального старения, которая достаточно часто встречается на практике, но теоретически исследована слабо. Это моральное старение, связанное с деградацией возможностей восстановления работоспособности элементов технической и технологической структур ПРИС при отказах. Назовем такое моральное старение моральным старением третьего рода. Если в случае морального старения второго рода информационная система не может удовлетворять изменившимся требованиям, то в данном случае она не может эффективно функционировать в условиях появления отказов оборудования, так как восстановление работоспособности затрудняется поиском запасных элементов, необходимостью применения устаревших технологий ремонта, отсутствием специалистов по ремонту оборудования и пр. [4]. В итоге ПРИС переходит в предельное состояние неустранимого отказа. Таким образом, под моральным старением третьего рода будем понимать деградацию (устойчивое снижение) возможностей восстановления способности информационной системы решать требуемые функциональные задачи с требуемыми характеристиками качества в условиях возникновения отказов оборудования.
Цель исследования
Для того чтобы иметь возможность прогнозировать показатели долговечности информационных систем в условиях действия процесса морального старения третьего рода, необходимо разработать соответствующую математическую модель.
Материал и методы исследования
Рассмотрим трёхуровневую иерархическую модель «система – подсистема – элемент», описывающую закономерности, лежащие в основе причинно-следственных связей, приводящих к возникновению предельного состояния оборудования прикладных распределенных информационных систем при моральном старении третьего рода.
Интегрированной структурной моделью достижения предельного состояния ПРИС будем называть логико-вероятностную модель причинно-следственных связей между переходом ПРИС в предельное состояние и совокупностью начальных и промежуточных событий, отражающих изменение состояния, как самих элементов информационной системы, так и элементов подсистемы восстановления технического ресурса (ПВТР). В качестве приемлемого класса моделей для моделирования морального старения третьего рода могут быть использованы логико-вероятностные модели деревьев предельных состояний (ДПС), которые применительно к задачам прогнозирования долговечности сложных восстанавливаемых систем впервые предложены и описаны в статье [2], а методы их анализа, основываются на результатах, представленных в монографиях [3, 5].
Разработка модели
Пусть задана некоторая функция (однозначно определяемая по ДПС)
Р(t) = r(Ps1, Ps1,..., Psk,..., Psm, t) (1)
зависимости вероятности недостижения предельного состояния (ВНПС) прикладной распределенной информационной системы от соответствующих вероятностей для подсистем, входящих в состав ПРИС.
При равной роли подсистем в обеспечении нормального функционирования ПРИС и отсутствии резервирования на уровне подсистем функция (1) принимает вид:
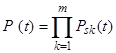. (2)
Общим свойством функции (1) является её монотонность, вследствие чего моделируемая структура относится к классу монотонных структур. Функция (1) является функцией многих переменных. С достаточной степенью приближения изменение ВНПС ПРИС может быть описано как: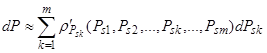 
.
Назовём величину 
ресурсной значимостью k-й подсистемы ПРИС, а величину произведения 
– ресурсным вкладом k-й подсистемы в изменение ВНПС системы. Обозначим ресурсную значимость подсистемы как 
, а ресурсный вклад как 
, тогда
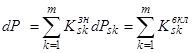, (3)
т.е. изменение ВНПС системы равно сумме ресурсных вкладов составляющих ее подсистем.
Обозначим вероятность безотказной работы i-го элемента k-й подсистемы как pik, а вероятность нормального функционирования j-го элемента ПВТР k-й подсистемы как rjk. Под вероятностью нормального функционирования j-го элемента ПВТР будем понимать вероятность выполнения конкретного условия, способствующего восстановлению работоспособности ПРИС при отказе ее элементов, например, вероятность наличия в ЗИП элемента, аналогичного отказавшему; вероятность проведения ремонта отказавшего элемента; вероятность пополнения ЗИП в случае исчерпания и т.п.
Тогда по соответствующей k-й системе ветви ДПС можно найти выражение для ВНПС k-й подсистемы
, (4)
где 
– вектор вероятностей безотказной работы элементов k-й подсистемы; 
– вектор вероятностей нормального функционирования элементов ПВТР, соответствующих (по ДПС) k-й подсистеме ПРИС.
Обозначим 
– множество индексов, соответствующих элементам pik, i = 
, и 
– множество индексов, соответствующее элементам rjk, j = 
. Тогда можно записать:
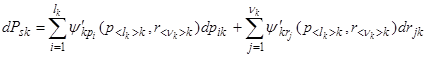. (5)
где 
; 
.
Или
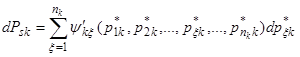. (6)
где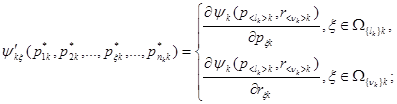
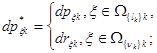nk = lk + nk.
Назовём величину 
ресурсной значимостью i-го элемента k-й подсистемы, а её произведение на dpik – ресурсным вкладом i-го элемента в изменение ВНПС k-й подсистемы.
Соответственно, назовём величину 
ресурсной значимостью j-го элемента системы восстановления технического ресурса k-й подсистемы, а её произведение на drjk – ресурсным вкладом j-го элемента ПВТР в изменение ВНПС k-й подсистемы.
Обозначим ресурсную значимость i-го элемента k-й подсистемы как 
, ресурсную значимость j-го элемента ПВТР k-й подсистемы как 
, ресурсный вклад i-го элемента k-й подсистемы как 
, ресурсный вклад j-го элемента ПВТР как 
. Тогда можно записать
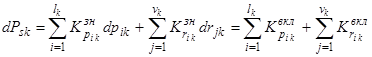, (7)
т.е. изменение ВНПС k-й подсистемы ПРИС равно сумме ресурсных вкладов её элементов и ресурсных вкладов элементов ПВТР, задействованных при восстановлении технического ресурса k-й подсистемы.
Подставив (7) в (3), получим
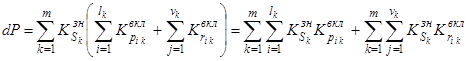, (8)
или, с учётом того, что =dpik, =drjk,
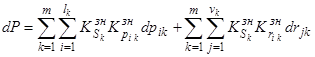. (9)
Из анализа общего вида выражения (9) видно, что изменение ВНПС системы определяется двумя основными составляющими:
, (10)
где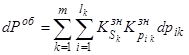 
– интегральная составляющая изменения ВНПС собственно объекта эксплуатации (ПРИС), обусловленная изменением технического состояния ее собственных элементов, а 
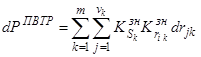– интегральная составляющая изменения ВНПС объекта из-за влияния системы восстановления технического ресурса.
Введём в рассмотрение W – полное множество индексов элементов системы: 
. Базовыми элементами будем называть такие элементы ПРИС, восстановление технического ресурса которых невозможно или не предусмотрено в течение жизненного цикла ПРИС (невозможен или не предусмотрен их ремонт, либо замена). Тогда можно записать:
W= WБ È WНБ, (11)
где WБ – подмножество индексов базовых, а WНБ – соответственно, небазовых элементов системы. С учётом (10) имеем:
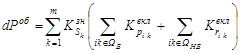
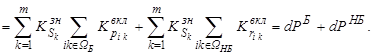(12)
Подставив (12) в (10), получим
. (13)
Обозначим относительный дифференциальный вклад базовых элементов в dP как
. (14)
С учётом (9) и (12) выражение (14) можно представить в виде:
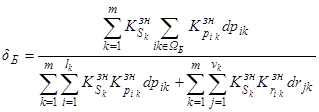. (15)
Определим входящие в (15) ресурсные значимости 
, и . В соответствии с выражением (2) ресурсная значимость k-й подсистемы ПРИС равна:
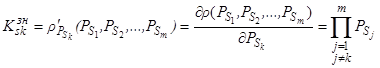. (16)
В соответствии с подходом к нахождению частных производных от функции многих переменных произвольного вида, описанным в [6], ресурсная значимость элемента pik равна:
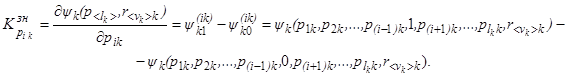(17)
Аналогично, ресурсная значимость элемента rik подсистемы восстановления технического ресурса элементов k-й подсистемы ПРИС определится выражением:
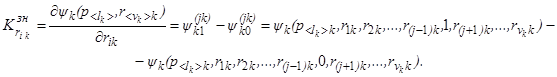(18)
Подставив (15), (16) и (17) в формулу (14), получим окончательное выражение для оценивания величины относительного дифференциального вклада базовых элементов в dP:
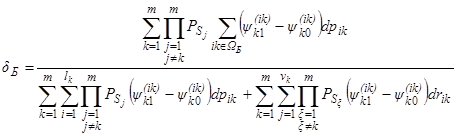, (19)
где 
. (20)
Аналогичным образом можно получить выражение для оценивания относительного дифференциального вклада элементов ПВТР:
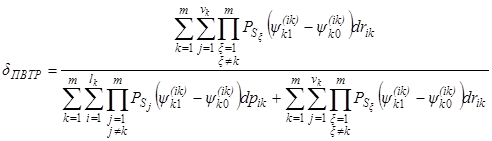, (21)
Нетрудно заметить, что и выражение (19), и выражение (21) зависят от одних и тех же аргументов, т.е. можно записать:
, (22)
, (23)
где F1(×) и F2(×) есть функциональные зависимости, вид которых определяется правыми частями выражений (19) и (21) соответственно.
Таким образом, так как общий вид функций F1(×) и F2(×) задан, для оценивания относительных дифференциальных вкладов dБ и dПВТР достаточно оценить абсолютные значения соответствующих вероятностей 
и их изменений во времени 
и 
, характеризующих фактическое состояние элементов ПРИС и ее ПВТР в момент контроля t = t0, причём:
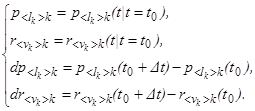(24)
Оценки значений соответствующих вероятностей могут быть получены с помощью моделей нижнего уровня иерархии интегрированной структурной модели предельного состояния ПРИС (см. рис.1).
Рис. 1. Иерархическая древовидная структура полимодельного комплекса прогнозирования остаточного срока службы ПРИС по критерию
морального старения третьего рода
Используя результаты регулярного контроля технического состояния элементов ПРИС в процессе эксплуатации, а также результаты оценивания состояния элементов ПВТР, можно отслеживать и прогнозировать динамику изменения значений относительных дифференциальных вкладов dБ(t) и dПВТР(t).
Представим изменение ВНПС системы в виде dP = dБ dP +dНБ dP+dПВТР dP, или
dP = (dБ +dПВТР)dP +(1–dБ –dПВТР)dP. (25)
Первое слагаемое правой части выражения (25) характеризует необратимую составляющую изменения ВНПС, второе слагаемое – обратимую составляющую.
Необратимость изменения ВНПС системы обусловливается двумя основными причинами: неполнотой восстановления ресурса ПРИС из-за наличия в ее составе базовых элементов, ресурс которых по технологическим, организационным, временным и финансовым причинам может быть восстановлен только при проведении капитального ремонта ПРИС; ограничениями восстановления ресурса ПРИС в части небазовых элементов из-за снижения потенциальных возможностей ПВТР с течением времени эксплуатации.
Таким образом, выражение (25) в дифференциальной форме отражает соотношение вкладов восстанавливаемого и невосстанавливаемого оборудования в ВНПС системы с учётом реальных возможностей системы восстановления технического ресурса.
Результаты исследования и их обсуждение
Рассмотрим возможность получения прогнозных оценок показателей морального ресурса третьего рода на основе данных о динамике изменения относительных дифференциальных вкладов dБ(t) и dПВТР(t).
Изменение ВНПС ПРИС на достаточно малом интервале 
определяется как
. (26)
Тогда имеем:
= (-1)
, (27)
где 
– безусловная (без учета возможности полного восстановления ресурса небазовых элементов) плотность распределения случайной величины 
(остаточного срока службы ПРИС до наступления предельного состояния по критерию морального старения третьего рода).
Необратимая составляющая ВНПС, согласно (25), может быть определена как 
=
или с учетом (27) как:
= (-1)
. (28)
С учетом (28) величина необратимого изменения ВНПС на произвольном интервале времени (
) может быть вычислена как:
(-1)
. (29)
Принимая во внимание, что минимально допустимый уровень ВНПС обычно задается некоторой величиной 
(гамма), имеем:
, (30)
где 
есть значение оценки гамма-процентного остаточного срока службы ПРИС до наступления предельного состояния по критерию морального старения третьего рода.
Подставив (29) в (30,) получаем уравнение
(-1)
, или 
, (31)
Данное уравнение назовем интегральным уравнением морального старения третьего рода. В частном случае (на самом деле достаточно распространенном на практике) имеем 
=0. Тогда уравнение (31) преобразуется к частному виду
. (32)
В общем случае аналитическое решение уравнений (31) и (32) достаточно сложно. Поэтому актуальным является решение данных уравнений приближенным численным способом, сущность которого рассмотрим ниже.
Пусть по результатам прогнозирования изменения вероятностей построена функция ВНПС системы P (t):
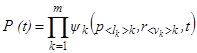. (33)
Пусть также на некотором интервале (ti, tj) изменение ВНПС составило величину
DP (ti; tj) = P (ti)– P (tj). (34)
Тогда интегральный вклад базовых элементов системы в изменение ВНПС (34) может быть определён как:
, (35)
где Dt – некоторый (достаточно малый) участок интервала (ti; tj).
По аналогии интегральный вклад элементов ПВТР в данном случае равен
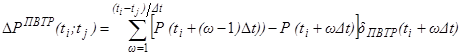(36)
Суммируя интегральные вклады (35) и (36), получим окончательное выражение для интегрального вклада необратимой (невосстанавливаемой) компоненты изменения ВНПС на интервале (ti; tj)
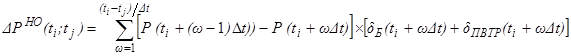. (37)
Зададимся некоторым предельным уровнем g
, ограничивающим снизу интервал возможных изменений ВНПС. Рассмотрим рис. 2. При достижении функцией работоспособности (ФР) 
(где 
) уровня g соответствующая этому событию наработка ПРИС составит 
, 
=0. Допустим, что в этот момент (на шаге 
=1) технический ресурс всех небазовых элементов ПРИС восстановлен до уровня, обеспеченного текущим состоянием ПВТР.
Рис.2. Изменение во времени условной ресурсной кривой
морального старения третьего рода информационной системы
Тогда, естественно предположить, что ФР системы возрастёт в данной точке на величину 
, т.е. до уровня 
=1–
.
При дальнейшем изменении функция 
= Р2(t)= 
+ + 1–g также пересечёт заданный предельный уровень g в некоторой другой точке 
. Проведение в момент (на шаге =2) восстановления технического ресурса небазовых элементов снова позволит повысить ВНПС, но уже до более низкого, чем в предыдущем случае, значения 
= 1–
– 
при общей суммарной наработке, равной 
, где 
.
Эксплуатация ПРИС по описанному алгоритму будет продолжаться до исчерпания возможностей восстановления технического ресурса (т.е. до того момента, когда величина достигаемого повышения ФР системы относительно заданного уровня g уже не может быть обеспечена выше некоторого порога e). Результирующая зависимость ФР от времени (наработки) в данном случае будет иметь вид пилообразной кривой с уменьшающейся высотой пиков. Так как данная кривая получена при условии восстановления технического ресурса небазовых элементов в пределах текущих возможностей ПВТР на момент достижения уровня g, то соответствующую ей ВНПС будем называть условной ФР системы.
Приведём выражение для условной ФР:
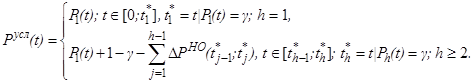(38)
Максимальное число шагов восстановления ресурса ПРИС до перехода в предельное состояние по критерию морального старения третьего рода определяется выражением
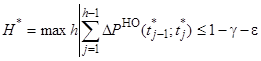. (39)
Тогда приближенная оценка гамма-процентного срока службы ПРИС до перехода в предельное состояние по критерию морального старения третьего рода может быть найдена как
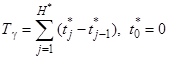. (40)
В некоторых ситуациях текущие возможности ПВТР на интервале упреждения прогноза можно приближенно описать, заменив в выражении (4) компоненты векторов 
значениями бинарной переменной [0;1] («0», если по оценке экспертов на предстоящем интервале эксплуатации рассматриваемый элемент ПВТР будет функционировать неудовлетворительно, и «1» – в противном случае).
Тогда при полной деградации ПВТР (т.е. при 
) оценка минимального гамма-процентного срока службы ПРИС определяется выражением
= (41)
При идеальной ПВТР (при 
=
) получаем оценку максимально достижимого гамма-процентного срока службы ПРИС:
= (42)
В этом случае, если ПРИС не содержит базовых элементов, т.е. 
=0, ее моральный остаточный ресурс третьего рода теоретически неограничен.
Выводы
В статье рассмотрены вопросы разработки математической модели прогнозирования показателей моральной долговечности оборудования прикладных распределенных информационных систем с деградирующей подсистемой восстановления технического ресурса. Модель базируется на основе динамического многомодельного учета вкладов различных групп элементов оборудования информационной системы и подсистемы восстановления ее технического ресурса в изменение вероятности недостижения предельного состояния. Приведено полученное впервые аналитическое выражение, позволяющее в общем виде оценить величину гамма-процентного остаточного срока службы информационной системы, как решение интегрального уравнения морального старения третьего рода. Описан способ итерационного приближенного решения данного уравнения. Получены выражения для оценивания предельных значений показателей моральной долговечности информационной системы, как при идеальной подсистеме восстановления ресурса, так и при полном ее отсутствии.
Рецензенты:
Козлов В.В., д.т.н., профессор, профессор кафедры ФГКВОУ ВПО «Военно-космическая академия имени А.Ф. Можайского» Министерства обороны РФ, г. Санкт-Петербург.
Смагин В.А., д.т.н., профессор, профессор кафедры ФГКВОУ ВПО «Военно-космическая академия имени А.Ф.Можайского» Министерства обороны РФ, г. Санкт-Петербург.