Введение. Использование вейвлетов в задачах обработки и распознавания речи продиктовано особенностями речевого акустического сигнала. Вейвлеты как средство многомасштабного анализа позволяют выделять одновременно как основные характеристики сигнала, так и короткоживущие высокочастотные составляющие в речевом сигнале, которые существенно влияют на качество произношения.
Люди с врожденной глухотой, но с не нарушенным речевым аппаратом имеют возможность научиться говорить и не являются истинно глухонемыми. Их немота обусловлена тем, что они не слышат звуки, которые произносят, что и является основной трудностью при обучении их речи. Представленная система дает глухонемым возможность обучения правильному произношению фонем [5].
Целью написания данной статьи является описание метода распознавания искаженных фонем с помощью вейвлет-преобразования. Сейчас 3 % людей в обществе являются глухонемыми, их немота обусловлена тем, что они не слышат произносимые ими звуки. Эти люди с ограниченными возможностями произношения сталкиваются с серьезными проблемами в общении с другими людьми. С помощью рассмотренного в статье метода можно создать систему, которая поможет глухонемым общаться, понимать и быть понятыми окружающими людьми, без знания сложных аспектов дактильной и жестовой речи [4].
Таким образом, появляется возможность самостоятельного обучения глухонемых правильному произношению звуков речи в домашней обстановке или в школе для детей при наличии компьютера.
Устройство человеческого уха. Внутреннее ухо человека представляет собой сложный лабиринт соединенных друг с другом каналов, которые расположены в височной кости и заполнены специальной жидкостью. Часть этого лабиринта образует вестибулярную систему, а одна из костных структур, имеющая форму спирали, относится к слуховой системе и называется улиткой.
В улитке происходит преобразование механических процессов в нервные сигналы, которые затем передаются в мозг и анализируются.
При передаче звуковых колебаний основание стремечка в такт с изменением звукового давления вдавливает мембрану овального окна в жидкость вестибулярного канала, создавая в нем избыточное давление, которое практически мгновенно распространяется по всей длине улитки. При этом с информационной точки зрения со звуком происходят определенные преобразования, которые сводятся в основном к усилению. Таким образом, большинство элементов в улитке имеют определенный коэффициент усиления k. Увеличение давления приводит в движение податливые структуры среднего канала – Рейснерову мембрану, жидкость среднего канала и базилярную мембрану, что, в свою очередь, вызывает изменение давления жидкости в тимпанальном канале и смещение мембраны круглого окна. Реакция базилярной мембраны на отдельный импульс увеличения давления в жидкости улитки не является мгновенной и может быть описана следующим образом. Сначала мембрана «выбухает» в сторону тимпанального канала у своего основания, затем в силу эластичности возвращается в положение равновесия. Возникшее выбухание перемещается вдоль длины мембраны к вершине за время, равное нескольким мс. Таким образом, на мембране возникает бегущая волна смещения ее локальных участков относительно положения, которые они занимают вне звука.
Реакция базилярной мембраны на частоту звуковых колебаний является следствием ее упругих свойств и анатомического строения. Разные участки мембраны отличаются шириной и жесткостью. Ширина мембраны увеличивается по направлению от основания к вершине примерно в десять раз, а упругость постепенно уменьшается: у основания мембрана более чем в 100 раз жестче, чем у вершины. Приблизительно половина мембраны, считая от ее вершины, реагирует на колебания с частотами от 0 до 2000Гц, в то время как оставшаяся часть (у основания) реагирует на остальные частоты звукового диапазона. Такое распределение означает, что различия между звуками в области низких частот обнаруживаются слуховой системой гораздо лучше, чем различия в высоких частотах. Можно сказать, что реакция мембраны на частоту сигнала приблизительно следует логарифмической шкале.
Интенсивность звука также влияет на колебательный процесс, возникающий в мембране: чем сильнее звук, тем больше размах колебаний всех участков мембраны, в том числе и участка с максимальным смещением. Размер зоны возбуждения вблизи точки максимального смещения определяется как частотой звука, так и его амплитудой. Связь местонахождения максимального возбуждения базилярной мембраны с частотой звука свидетельствует о частотно-избирательной или фильтрующей функции этого слухового органа, в физиологии слуха связь между местом максимального смещения базилярной мембраны и частотой возбуждающего сигнала называют тонотопическойорганизацией. Этот же термин распространяется и на более высокие уровни слуховой системы для обозначения пространственной упорядоченности нервных элементов в соответствии с их частотной избирательностью [7].
Таким образом, во внутреннем ухе человека осуществляется перекодирование частоты и интенсивности звукового сигнала в активность, локализованную на определенном участке базилярной мембраны. Различные участки мембраны являются своеобразными биомеханическими фильтрами, а мембрана в целом может рассматриваться как набор фильтров, упорядоченных по частоте и покрывающих в совокупности всю область частот, доступных восприятию человека. В техническом спектральном анализе фильтр является устройством, которое, обрабатывая сигнал, пропускает колебания только определенных частот. Результирующее преобразование сигнала во внутреннем ухе человека с точностью до константы совпадает с вейвлет-преобразованием сигнала. Следовательно, восприятие человеческим ухом звуковых колебаний, и в том числе человеческой речи, с математической точки зрения соответствует вейвлет-разложению. Поэтому естественно в системе распознавания речи использовать вейвлет-разложение [6].
Вейвлет-преобразование речевого сигнала
Вейвлет-преобразования одномерного сигнала (формула 1) – это его представление в виде обобщенного ряда или интеграла Фурье по системе базисных функций, сконструированных из материнского вейвлета ψ(t), обладающего определенными свойствами за счет операций сдвига во времени b и изменения временного масштаба a. Множитель 1/√a обеспечивает независимость нормы этих функций от масштабирующего числа a.
![]() (1)
(1)
Для заданных значений параметров a и b функция ψab(t) и есть вейвлет, порождаемый материнским вейвлетом [8].
В частотной области вейвлеты похожи на всплески с пиком на частоте w0, то есть имеют вид полосового фильтра, при этом w0 и ∆w уменьшаются с ростом параметра a.
Следовательно, вейвлеты локализованы как во временной, так и частотной областях.
Вейвлет-преобразование обеспечивает двумерное представление исследуемого сигнала в частотной области в плоскости частота-положение. Аналогом частоты при этом является масштаб аргумента базисной функции – времени, а положение характеризуется ее сдвигом. Это позволяет разделять крупные и мелкие особенности сигналов, одновременно локализуя их на временной шкале. Иными словами, вейвлет-анализ можно охарактеризовать как спектральный анализ локальных возмущений.
Спектральное представление вейвлетов аналогично заданию окна в оконном преобразовании Фурье. Но отличие состоит в том, что свойства окна, его ширина и перемещение по частоте, присущи самим вейвлетам. Это служит предпосылкой их адаптации к сигналам, представляемым совокупностью вейвлетов. Поэтому с помощью вейвлетов можно осуществить анализ и синтез локальной особенности речевого сигнала.
Вейвлет-преобразование не просто «режет» исследуемый объект на куски, а выделяет из него компоненты разных масштабов, и каждая компонента анализируется с той степенью детальности, которая соответствует его масштабу. Следовательно, вейвлет-преобразование можно использовать для обработки нестационарных сигналов, которым и является речевой сигнал.
Представим речевой сигнал как функцию f из бесконечно мерного Гильбертова пространства L2(R). Эту функцию f разложим на некотором заданном уровне разрешения jn, (где n=1,2,3…) в ряд вида, представленного формулой 2.
![]() (2)
(2)
где φjn,kи ψjn,k – масштабированные и смещенные версии скейлинг-функции (масштабной функции) φ и «материнского вейвлета»ψ; sj,k – коэффициенты аппроксимации; dj,k –детализирующие коэффициенты.
Вейвлет-коэффициенты аппроксимации соответствуют передаточной характеристике фильтра низких частот, а коэффициенты детализации соответствуют высокочастотному фильтру [2].
Вейвлет-коэффициенты sj,k и dj,k можно вычислить по формулам 3 и 4.
![]() (3)
(3)
![]() (4)
(4)
Первая сумма в (6) со скейлинг-функциями φj,k содержит средние значения f по диадным интервалам [к2-j, (к+1)2-j). Усреднение проводится с весовыми функциями φj,k(х). Второй член содержит все флуктуации f на данном интервале. Эти флуктуации проистекают из всех меньших интервалов, заключенных внутри данного и соответствующих большим значениям параметра масштабирования f. Можно сказать, что этот член как бы фокусирует наше внимание на все более тонких деталях изучаемого сигнала. Это последовательное изучение свойств сигнала происходит через равные промежутки, как следует из постоянства масштабирующего множителя, причем детали размером 2-j располагаются в точках k2-j. На низшем уровне разрешения j0, наиболее широких интервалах, первая сумма содержит всего один член, дающий общее усредненное взвешенное значение сигнала ‹f›=sj0k0, где к0 обозначает центр гистограммы. Вторая сумма в (6) показывает флуктуации на всех без исключения уровнях. На следующем уровне с более мелким разбиением j1>jо в первой сумме содержатся два члена, отвечающих за средние значения f в полуинтервалах с центрами, расположенными в к1, к2. Число членов во второй сумме уменьшается на единицу – исчезает член, который раньше показывал величину флуктуаций на половинном масштабе. Общее число членов в разложении остается неизменным. Число членов в каждой сумме зависит от выбранного уровня разрешения. Меняя на единицу этот уровень, мы передвигаем некоторые члены в другую сумму, причем каждое из этих представлений является истинным представлением исходной гистограммы на разных уровнях разрешения [3].
Экспериментальные исследования. В процессе исследования фонем были проведены эксперименты в системе Matlab, в результате которых были выделены характерные признаки каждой из фонем, представленных с помощью вейвлет-преобразования [1]. В следующих таблицах приведены вектора из восьми коэффициентов, которые представляют собой средние значения энергий детализирующих коэффициентов, рассчитанные на каждом уровне вейвлет-разложения. Жирным шрифтом выделены характерные особенности каждой из фонем.
Таблица. Вектора средних значений энергий детализирующих коэффициентов, рассчитанные на каждом уровне вейвлет-разложения для фонем ‘а’, ‘и’, ‘о’
|
a1 |
и2 |
o1 |
|
1.0e+003 |
1.0e+003 1.0e+003 |
1.0e+003 1.0e+003 * |
|
0.0020 |
0.0142 |
0.0001 |
|
0.0117 |
0.0575 |
0.0006 |
|
0.1657 |
0.0099 |
0.0041 |
|
5.1521 |
0.0231 |
0.2986 |
|
0.7928 |
0.1897 |
7.1588 |
|
0.3462 |
2.8531 |
0.2790 |
|
0.0895 |
0.0623 |
0.0159 |
|
0.0388 |
0.0081 |
0.0133 |
Из таблицы видно, что вейвлет-преобразование методом многомасштабного вейвлет-анализа позволяет выявить характерные признаки каждой фонемы, также как это происходит на базилярной мембране внутреннего уха человека. Затем вектора подаются на вход нейросети и распознаются, так же как в человеческом мозге. Следовательно, предложенная система работает по алгоритму человеческого уха, идеальной системы распознавания фонем созданной самой природой.
На рисунке 1 показаны результаты распознавания фонем системой с помощью оконного преобразования Фурье.
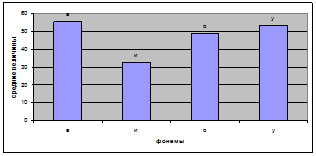
Рисунок 1. График средних арифметических не взвешенных величин результатов распознавания фонем ‘а’, ‘и’, ‘о’, ‘у’ нескольких людей одного пола системой, использующей оконное преобразование Фурье, обученной на фонемах одного из них
Из рисунка 3 следует, что предполагаемая модель и ее исполнение показали хорошие результаты правильности распознавания фонем, но все средние величины результатов распознавания меньше шестидесяти. Это обусловлено тем, что метод Фурье преобразования не решает проблему дикторозависимости системы. Следовательно, все системы, построенные на преобразовании Фурье, являются дикторозависимыми, то есть предназначены для работы только с одним пользователем, на фонемах которого обучалась данная система. Однако в нашем случае это невозможно, так как человек, чьи фонемы должна распознавать система, не может правильно произнести их.
На следующем рисунке 2 приведены результаты распознавания фонем системой с помощью вейвлет-преобразований.
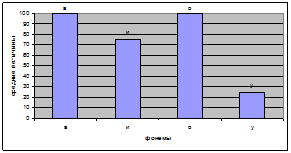
Рисунок 2. График средних арифметических не взвешенных величин результатов распознавания фонем ‘а’, ‘и’, ‘о’, ‘у’ нескольких людей одного пола системой, использующей вейвлет-преобразование, обученной на фонемах одного из них
Из рисунка 4 видно, что система, основанная на методе вейвлет-преобразования, близка к дикторонезависимым, что для решения нашей задачи является необходимым. Система обучается на векторах фонем правильного произношения, а затем распознает искаженное произношение этой фонемы.
Заключение. В результате проделанной работы можно сделать вывод, что вейвлет-анализ как средство многомасштабного анализа может быть успешно применен для исследования особенностей речевого сигнала. Исходя из результатов эксперимента, можно сказать, что при использовании вейвлет-преобразования для решения задач распознавания речи процент распознавания фонем гораздо выше, чем при использовании преобразования Фурье. Это объясняется тем, что вейвлет-преобразование гораздо ближе к естественному восприятию звука человеческим ухом.
Рецензенты:
Кузнецов А.Е., д.т.н., профессор, заместитель директора научно-исследовательского института обработки аэрокосмических изображений (НИИ «Фотон»), г. Рязань.
Мусолин А.К., д.т.н., профессор, зав. кафедрой АИТП Рязанского государственного радиотехнического университета, г. Рязань.



