Новая стратегия построения школьного курса математики, заданная Федеральным государственным образовательным стандартом среднего (полного) общего образования от 2012 г. (ФГОС третьего поколения), предполагает создания условий для развития и самореализации обучающихся, их самоидентификацию посредством личностно и общественно значимой деятельности, социального и гражданского становления, в том числе через реализацию образовательных программ, входящих в основную образовательную программу. Таким образом, продолжена заданная в Концепции модернизации российского образования на период до 2020г. траектория, направленная на профилизацию обучения, которая требует комплексных инноваций, как в сфере определения содержания математического образования, так и в сфере выбора методов обучения, соответствующих высоким целям формирования конкурентно-способной, гармоничной личности ученика, будущего специалиста и абитуриента вуза. Поэтому приведение в соответствие с поставленными задачами процесса обучения математике в средней общеобразовательной школе является важнейшей проблемой, требующей скорейшего решения.
В ФГОС среднего (полного) общего образования выделяются требования к формированию ИКТ:
- компетентности обучающихся, которая, согласно примерной основной образовательной программе, должна формироваться в рамках различных предметов, в том числе и математики. Следовательно, перед нами напрямую встает задача рационального применения информационных и коммуникационных технологий (ИКТ) при обучении математике на всех этапах. Но это применение должно идти не спонтанно, а регулярно и целенаправленно, в зависимости от того, на каком уровне владения ИКТ находятся ученики и на каком профиле они обучаются.
Вопросы методики преподавания математики с использованием ИКТ тесно связаны с вопросами информатизации образования. Сама проблема информатизации математического образования разрабатывается достаточно давно, среди авторов можно отметить В.В. Беспалько, С.А. Бешенков, Ю.С. Барановский, Я.А. Ваграменко, И.Е. Вострокнутов, М.А. Гаврилова, Б.С. Гершунский, О.А. Козлов, Г.А. Кручинина, А.А. Кузнецов, Е.И. Машбиц, В.М. Монахов, И.В. Роберт и др. Но вопрос эффективного использования ИКТ в зависимости от выбранного профиля обучения математике в старшей школе ранее широко не раскрывался.
На старшей ступени выделены несколько профилей, в которых математика попадает в профильные предметы: физико-математический, физико-химический, информационно-технологический, а также в базовые предметы: социально-гуманитарный, филологический.
Анализ существующих методических разработок по проведению урока в старших классах с использованием ИКТ показывает, что на современном этапе развития образование существует большое количество компьютерных средств обучения различного методического назначения: обучающие, развивающие, исследовательские, тренинговые, контролирующие и другие классы программных средств ИКТ. Существуют различные классификации электронных программных средств образовательного назначения (А.А. Кузнецов, В.М. Монахов, И.В. Роберт, и др.). Обобщив множество существующих классификаций, мы предлагаем следующую:
- информационно-справочные системы (для оперативного поиска информации по запросу: электронные библиотеки, распределенные и централизованные издательские системы, сайты научно-образовательных проектов, базы данных по отраслям знаний)
- электронные обучающие программы, включающие в себя электронные учебники, тренажеры, тьюторы, лабораторные практикумы, тестовые системы, прикладные программы;
- интерактивные программные средства;
- обучающие системы на базе мультимедиа-технологий, построенные с использованием персональных компьютеров, планшетных компьютеров, видеотехники, проекторов, мультимедиа систем;
- интеллектуальные и обучающие экспертные системы, используемые в различных предметных областях;
- средства телекоммуникации, включающие в себя электронную почту, телеконференции, локальные и региональные сети связи, сети обмена данными и т.д.
Каждый представленный в классификации вид программного средства может быть использован на различных этапах образовательного процесса, как при подготовке учителя и ученика к уроку, так и при проведении различного вида занятий. Для достижения высокой продуктивности обучения требуется рациональная интеграция средств ИКТ в современный урок математики с учетом его специфики и вариативности. На схеме 1 представлен возможный вариант применения указанных видов ИКТ в различных темах курса математики старшей школы.
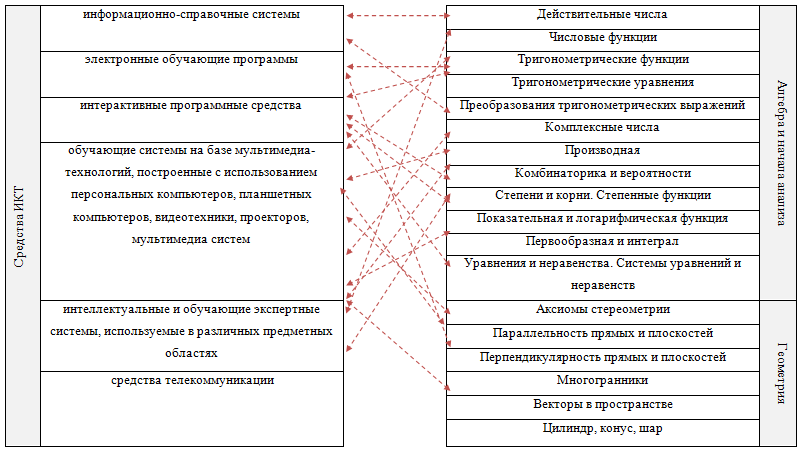
Схема 1. Рациональная интеграция средств ИКТ в курс математики старшей школы
Проблема эффективной организации и методической поддержки профильного обучения математике, в том числе и средствами современных информационных и коммуникационных технологий, является одной из актуальных проблем, стоящих перед современной методической наукой. Особое внимание нужно уделить классам с гуманитарным наклоном. Значение изучения математике в таких классах, может оказаться даже больше, чем в специализированных. Учащиеся гуманитарных классов могут испытывать трудности при работе с теоретическим материалом, так как стремятся видеть конкретное применение, а не обобщенные методы, им может быть свойственна пониженная логическая грамотность, склонность к эмоциональным оценкам, познавательная активность больше нацелена на приобретение новых знаний, а не на использование уже имеющихся. Именно использование ИКТ в данных классах, мотивирует учащихся на исследовательскую деятельность, проявление творческих аспектов при выполнении математических действий, способствует лучшему усвоению теоретического материала.
Для рациональной организации работы на уроке математики нами выделены цели использования ИКТ в гуманитарных профилях:
- Повысить интерес к изучаемому предмету за счет использования различных интерактивных ресурсов.
- Стимулировать активность учащихся в области изучения математике.
- Показать связь математики с другими науками, прежде всего, ведущими для выбранного профиля.
- Изменить формы проведения урока с целью усиления практического компонента (урок-демонстрация).
- Организовать доступ к электронным библиотекам, энциклопедиям, электронным версиям словарей, информационно-справочным сайтам и т.д.
- Развить пространственные представления за счет демонстрации виртуальных моделей, в том числе из галереи фигур.
Рассмотрим подробнее реализацию нескольких целей рационального использования ИКТ на уроке математики с применением интерактивной программной среды GeoGebra. Приведем фрагмент урока по геометрии в 11 классе, тема: «Построение сечений».
Выбор этого программного средства не случаен. GeoGebra – бесплатная программа предоставляющая возможность создания динамических («живых») чертежей для использования на разных уровнях обучения геометрии, алгебры, планиметрии и других смежных дисциплин. В отличие от других программ для динамического манипулирования геометрическими объектами, идея GeoGebra заключается в интерактивном сочетании геометрического, алгебраического и числового представления.
Тема «Сечения» является одной из самых «проблемных» в гуманитарных классах, так как требует не только хорошей геометрической подготовки, но и развитого пространственного мышления, позволяющего представить секущую плоскость и геометрического тела, корректно изобразить сечение и, возможно, применить его к дальнейшему решению задачи.
Задача. Дан параллелепипед ABCDA1B1C1D1. На стороне B1C1 взята точка Р, а на стороне DC – точка K. Построить сечение куба плоскостью A1PK.
Решение:
Учитель заранее подготавливает шаблон параллелепипеда в интерактивной среде GeoGebra (Рис.1).
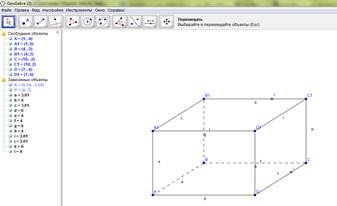
Рис.1. Интерфейс программной среды GeoGebra с шаблоном параллелепипеда.
Учитель предлагает учащимся выполнить построение:
1. Строим прямую A1P. С помощью инструмент – «Прямая по двум точкам» (Рис. 2) это выполняется проще, чем с помощью обычной линейки. Можно наглядно продемонстрировать, как «появляется» искомая прямая.
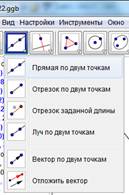
Рис.2. Панель инструментов программы GeoGebra.
2. Строим прямую, проходящую через точку K, параллельно A1P. Обозначим точку пересечения Е. Для этого тоже используются инструменты GeoGebra – «Параллельная прямая» (Рис. 2).
3. Соединяем точки А1 и Е также с помощью инструмента «Прямая по двум точкам» (Рис. 3).
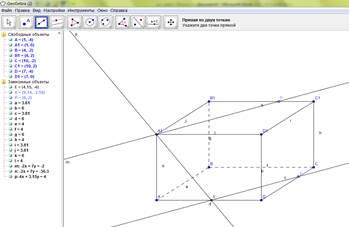
Рис.3. Построение прямой А1Е с помощью GeoGebra.
4. Строим прямую через точку Р, параллельно А1Е. G – точка пересечения этой прямой с ребром СС1. Построить точку нам поможет инструмент «Точка» (Рис.4).
5. Соединяем точки К и G. Сечение А1ЕКGP – искомое (Рис.5).
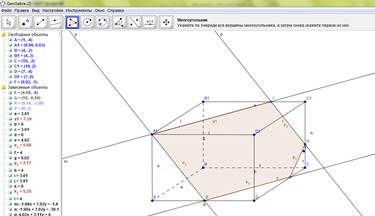
Рис. 5. Сечение А1ЕКGPв программной среде GeoGebra.
Далее учитель предлагает учащимся доказать правильность построения. Программа GeoGebra позволяет не только выполнить эти построения, но и «проиграть» их, то есть, продемонстрировать построение в динамике. Для этого используется инструмент «Проигрыватель».
В гуманитарных профилях у большинства школьников на уроке геометрии, возникает проблема с визуальным восприятием построения сечения геометрических фигур. Этим фрагментом урока мы показали, что для современного школьника, информация, представленная в интерактивной программной среде GeoGebra, воспринимается лучше, чем книжная. Положительный момент использования программы в том, что визуальное представление учебного материала делает его интересным, более информативным, понятным, убедительным, формирует пространственное воображение, способствует лучшему усвоению материала.
В итоге, можно сказать, что комплексная реализация поставленных целей использования ИКТ в гуманитарных профилях помогает, с одной стороны, более эффективному усвоению предмета, повышению интереса и мотивации, усилению практического компонента, развитию пространственных представлений и логического мышления, а с другой – формирует навыки работы с электронными ресурсами, которые необходимы для дальнейшего продолжения образования и профессиональной деятельности.
Рецензенты:
Родионов М.А., д.п.н., профессор, зав. кафедрой «Алгебра и методика обучения и воспитания математике и информатике» ФГБОУ ВПО «Пензенский государственный университет», г. Пенза
Садовников Н.В., д.п.н. профессор кафедры «Компьютерные технологии» ФГБОУ ВПО «Пензенский государственный университет», г. Пенза.



