Введение
Веб-сервисы выполняют обмены в сети и должны удовлетворять критериям качества обслуживания Quality of Service (QoS), которые зависят от вида сообщения. Провайдеры предлагают широкий выбор веб-сервисов с дублированием функций сервисов. Возникает задача выбора сервисов, выполняющих необходимую функцию и обеспечивающих требуемый уровень QoS. Задача выбора композиции сервисов по своей сути является комбинаторной. Большинство математических моделей этой проблемы приводят к NP-трудным задачам. Потребителю сервисов для построения композиции требуются линейные или хотя бы полиномиальные алгоритмы.
Материалы и методы исследования
При создании сложного веб-сервиса в реальных системах можно комбинировать его различными способами из имеющегося набора элементарных сервисов, первое упоминание задачи композиции веб-сервисов появилось в 2004 году [4]. В математической постановке задачи композиции сервисов строится векторная целевая функция по количеству критериев QoS. Ставится многокритериальная задача с ограничениями. В литературе приводится около 40 различных критериев качества для задачи композиции. Если указаны все возможные последовательности выполнения сервисов для реализации заданной функции, то рассматривается оптимизация на графе.
Задача оптимальной композиции сервисов входит в класс комбинаторных задач оптимизации. Моделируются задачи булева программирования, значения 1 или 0 переменных указывают, какие сервисы выбраны для композиции функции. Из Парето-оптимальных решений выбирается одно, для этого критерии задачи взвешенной суммой приводятся единственному. В [5, 6] такая задача решается в два этапа, на первом, локальном, из предложений провайдеров выбирается лучший набор сервисов, на втором, глобальном, по двум критериям выбирается Парето-оптимальное множество. Модели на графах принимают во внимание связи сервисов и ищут оптимальную цепь сервисов на сети. В [8] учтены 5 критериев качества: стоимость, затраты времени, надежность, доступность, рейтинг провайдера сервисов. На решение накладывают ограничения по времени и по стоимости сервисов. Для решения задачи на основе информации брокеров выбирается множество сервисов, выполняющих требуемую функцию, из него создается сеть выполнения работ. Из пяти критериев качества создается единственная целевая функция. Строится критический путь, сервисы которого дают решение. Модель оптимизации на графе рассматривается и в [7], здесь строится модель дискретного программирования в виде многомерной задаче о рюкзаке. Кроме графовой модели и дискретного программирования предлагаются другие подходы, например, моделирование сетью Петри, иерархическую модель доступа к сервисам.
Здесь рассматривается задача одновременной композиции нескольких сервисов.
Постановка задачи и математическая модель
Ставится задача композиции сложных веб-сервисов из наборов элементарных сервисов. Обычно информационная система имеет избыточных набор сервисов, которые частично или полностью дублируют функции друг друга. Сервисы публикуются в реестрах UDDI своих провайдеров, брокеры, программы поиска и предоставления услуг, выбирают требуемые сервисы, по критериям качества QoS формируя сложный сервис. Здесь решается задача композиции нескольких сложных сервисов (далее просто сервисов), для которых требуется выбрать оптимальные наборы атомарных сервисов (атомов). Даны структурные схемы наборов атомов, каждый реализует сервис. Математическую модель задачи представим как оптимизацию векторного критерия на ориентированном взвешенном графе без контуров. Задача может моделироваться и в рамках дискретного программирования.
Без потери общности будем рассматривать минимизацию критериев. Предполагается, что целевые функции определены на всех допустимых решениях задачи и монотонно возрастают. Если есть хотя бы одно допустимое решение, то существует и оптимальное решение. В этой работе многокритериальная задача взвешенной суммой критериев приводится к оптимизации с одной целевой функцией.
Формализуем задачу композиции. Далее будем называть ориентированный конечный граф, не содержащий контуров, сетью. Пусть задан пакет сервисов { S1, S2, … , SN}, которые требуется скомпоновать из доступных атомов. Атомы, связанные в структуры, выполняют заданные сервисы Sk. Структуры представлены сетями, узлы соответствуют событиям, дуги – атомам. Сеть не содержит контуров, то есть атомам нельзя составить цикл. Для повторов фрагмент графа копируется несколько раз.
На основании структур представления сервисов формируется сеть G = (N, A), где N – узлы, A – дуги. Узлы обозначим ti, дугу, связывающую узлы ti и tj обозначим (i, j), ей соответствует атом s(i, j). Сеть G сформирована из структурных связей атомов, которые формируют сервисы Sk, k = 1, 2, … , N. Для каждого k задана сеть Gk атомов, из которых можно сконструировать сервис Sk . Сеть G объединяет сети Gk , k = 1, 2, … , N. Если сети Gk попарно не пересекаются, то задача распадается на N более простых независимых. Положим, что сеть G состоит из одной компоненты. Если у нее несколько начальных узлов, то дополнением фиктивных дуг создадим единственный начальный узел, аналогично создадим единственный конечный узел. Атомы s(i, j) пометим числом Texec(i, j) – продолжительностью его выполнения, эта величина не зависит от Sk, и N-мерным вектором I(i, j), его компонента k равна 1, если атом s(i, j) принадлежит Gk, иначе компонента равна 0.
При распараллеливании сервисов, исходящих из события, возможны два различных случая, в одном случае необходимо выполнить все параллельные ветви (связь типа AND), в другом случае выполняется одна из параллельных ветвей (связь типа OR). Связи типа AND можно преобразовать в единую дугу, параллельные ветви атомов заменяются одним атомом. Будем предполагать, что в сети существуют только связи типа OR.
В сетевой постановке получаем задачу оптимизации нелинейной целевой функции на потоке заданной величины, с ограничениями на дугах. Допустимыми решениями задачи являются N полных цепей Ck, по числу сервисов Sk. Вводится NM булевых функций ![]() для дуг (i, j), где M – число дуг сети G . Отсчет времени начинается в момент t = 0, интервал определения функций [0, Tx] выбирается так, что в момент Tx заканчивается выполнение всех сервисов Sk. Если в момент t0 сервис Sk использует атом s(i, j), то
для дуг (i, j), где M – число дуг сети G . Отсчет времени начинается в момент t = 0, интервал определения функций [0, Tx] выбирается так, что в момент Tx заканчивается выполнение всех сервисов Sk. Если в момент t0 сервис Sk использует атом s(i, j), то ![]() = 1, иначе
= 1, иначе ![]() = 0. Атом не может одновременно обслуживать более одного сервиса, поэтому накладываем ограничения на пропускную способность дуг
= 0. Атом не может одновременно обслуживать более одного сервиса, поэтому накладываем ограничения на пропускную способность дуг

Таким образом, суммарные потоки единиц продуктов k на цепях Ck порождают суммарный поток с величиной N. Цепь Ck описывается функцией ![]() , которая повсюду равна 0, кроме интервала, на котором Sk использует сервис s(i, j), обозначим этот интервал [
, которая повсюду равна 0, кроме интервала, на котором Sk использует сервис s(i, j), обозначим этот интервал [![]() ,
, ![]() ), тогда
), тогда
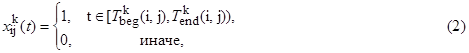
![]()
Необходимо учесть условие баланса потока в сети, для этого определим индикаторы атомов, зависящие от сервиса k и от дуги (i, j). Если атом s(i, j) был задействован при композиции Sk , то значение индикатора положим равным единице

Индикаторы позволяют ввести баланс потока в узлах сети, для любого узла n и любого сервиса k выполняется условие:
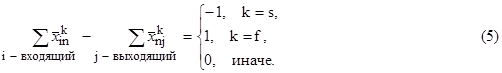
Это означает, что в промежуточных узлах поток, входящий в узел, равен выходящему.
Уточним критерии качества задачи. Пусть для каждого сервиса Sk. имеем L целевых функций, которые взвешенной суммой с положительными весами преобразованы в целевую функцию сервиса Sk. Повторением операции взвешенной суммы получаем единственную целевую функцию F(C1, C2, … , CN) для всех сервисов Sk. Так как все исходные критерии являются суммой параметров на s(i, j) и монотонно возрастают, то это свойство сохраняется и для F(×). Целевая функция является линейной

Ставится задача P найти функции ![]() , минимизирующие целевую функцию (6) при ограничениях (1) – (5) и дополнительным ограничением на время
, минимизирующие целевую функцию (6) при ограничениях (1) – (5) и дополнительным ограничением на время ![]() завершения работы сервисов цепей Ck, если Ck = ((ik1, ik2), … , (ik(m-1), ikm)), то
завершения работы сервисов цепей Ck, если Ck = ((ik1, ik2), … , (ik(m-1), ikm)), то
![]()
Метод решения
В заданном объединении сетей Gk k = 1, 2, … , N, требуется построить N полных цепей Ck, каждая из которых принадлежит сети Gk, цепь k соответствует календарному плану работ выполнения сложного сервиса Sk. Календарные планы дают решение задачи P. Задача композиции одного сервиса сводится к построению кратчайшей цепи, в модели дискретного программирования матрица ее ограничений унимодулярна, и она решается одним из стандартных методов теории сетей (см. [2], стр. 50).
При N > 1 между сложными сервисами возникает конкуренция за атомы и задача усложняется. Дискретная модель этой задачи содержит ограничения (1), (2) на функции, поэтому нельзя говорить о матрице ограничений [2].
Покажем, что к решению задачи P можно применить метод динамического программирования [3]. Метод можно применять к задаче, если на ее решениях выполняется принцип оптимальности: сужение оптимального решения от любой его точки до конца процесса само является оптимальным решением с началом в данной точке. В задаче P рассматриваются цепи, связывающие узлы ts и tf. Промежуточной точкой решения может служить произвольный разрез сети. Пусть имеем оптимальное решение задачи P . Выполним разрез и удалим его дуги, выберем компоненту, содержащую узел tf. Тогда сужением задачи построения полных циклов будет задача построения полных циклов на подсети из заданных узлов с заданными начальными условиями на исходные события. Очевидно, что ввиду суммарного представления целевой функции (6) сужение оптимального решения задачи P на подсети даст оптимальное решение задачи для подсети, иначе исходное оптимальное решение задачи P не оптимально. Таким образом, верно следующее утверждение.
Утверждение. Решение задачи P удовлетворяет принципу динамического программирования.
Применение этого метода возможно, однако для реальных задач требует большого перебора вариантов. Применение этого метода возможно, однако он требует большого перебора вариантов, сложность алгоритма экспоненциальна. Задачи небольшого размера можно решать методом динамического программирования. Здесь предлагается эвристический алгоритм решения задачи, основанный на методе параллельного расписания в классической задаче календарного планирования с ограничениями на ресурсы [1]. Алгоритм последовательно добавляет к каждой цепи Ck следующий атом, выбирая его как максимальный по целевой функции из допустимых исходящих дуг с текущим свободным резервом в заданном интервале. В случае если такой не найден, то выбирается наиболее ценный атом из тех, которые не нарушают ограничение на ресурс времени. Если же нет и таких работ, то делается шаг назад с удалением из рассмотрения пройденной дуги.
Пусть SET = {ti1, ti2, …, tiN} – текущие завершающие события уже найденных начальных дуг цепей Ck. На каждом шаге алгоритма оценивается возможность продолжения цепей из текущих состояний, то есть проверяются текущие критические пути из SET и строится новое множество SET с изменением всех его элементов.
Эвристический алгоритм решения задачи P.
Вход: Граф G, объединяющий сети Gk, k = 1, … , N, вектор директивных сроков T*, целевая функция F(×) (см. (6)).
Выход: Цепи Ck сетей Gk, k = 1, … , N, удовлетворяющие директивным срокам и приближающие целевую функцию F(×).
1. Положить все элементы SET равными ts.
2. Цикл по выбору следующей дуги цепи Ck. Положить k = 1.
3. Если tik = tf, то перейти к 7.
4. Найти критический путь в сети Gk с начальным узлом tik из множества SET, по заданному ![]() вычислить полный резерв R на событии tik. Если нет выбора дуг для поиска критического пути, то это означает, что нет цепи Ck, удовлетворяющей ограничениям задачи, выдать сообщение «нет решения для сервиса k», перейти к 8. Если полный резерв отрицательный, то есть нарушен директивный срок, то перейти к 6.
вычислить полный резерв R на событии tik. Если нет выбора дуг для поиска критического пути, то это означает, что нет цепи Ck, удовлетворяющей ограничениям задачи, выдать сообщение «нет решения для сервиса k», перейти к 8. Если полный резерв отрицательный, то есть нарушен директивный срок, то перейти к 6.
5. На множества дуг сети Gk, исходящих из tik, выбрать дуги, удовлетворяющие ограничениям задачи по критическому пути с обязательным условием включения рассматриваемой дуги, из этих дуг выбрать дугу с наименьшим значением целевой функции, пусть эта дуга ведет в узел j. Заменить SET tik на tj, перейти к 7.
6. Из узла tik вернуться к предыдущему узлу, удаляя дугу перехода из дальнейшего рассмотрения.
7. Положить k = k++, переходя к следующей цепи Ck.
8. Конец.
Эвристика алгоритма используется на шаге 5 выбора очередной дуги. Предложенный выбор гарантирует выполнение ограничений, но может не давать оптимального значения целевой функции. Сложность представленного алгоритма линейна, если гарантировано ограниченное применение шага 6. Таким образом, алгоритм имеет псевдолинейную сложность.
Обсуждение результата и заключение
Для сравнения двух методов были проведены 10 экспериментов с различными числами сервисов и атомов, в каждом эксперименте были случайным образом сгенерированы и решены по 50 задач. В таб. 1 приведены основные параметры задач и полученные результаты.
Таблица 1. Параметры задач и сравнение методов ДП и ЭМ
|
№ |
Колич. сервисов |
Кол. атомов в сетях |
Значение критерия |
Отклонение критерия (%) |
Изменение времени работы (%) |
||
|
Gk |
G |
ДП |
ЭМ |
||||
|
1 |
3 |
14 |
32 |
41 |
44 |
7.3 |
5.4 |
|
2 |
5 |
16 |
65 |
54 |
59 |
9.3 |
8.1 |
|
3 |
8 |
18 |
72 |
58 |
67 |
10.5 |
11.7 |
|
4 |
10 |
21 |
120 |
84 |
92 |
9.5 |
12.2 |
|
5 |
12 |
22 |
155 |
102 |
114 |
11.8 |
9.1 |
|
6 |
15 |
24 |
220 |
156 |
184 |
12.9 |
15.2 |
|
7 |
18 |
25 |
318 |
220 |
312 |
13.8 |
34.4 |
|
8 |
20 |
28 |
416 |
282 |
321 |
13.6 |
36.3 |
|
9 |
23 |
30 |
450 |
355 |
413 |
14.1 |
38.2 |
|
10 |
25 |
31 |
480 |
392 |
484 |
13.2 |
48.6 |
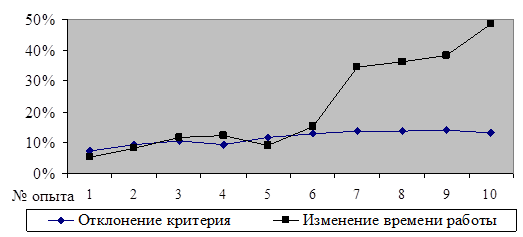
Рисунок 1. Сравнение отклонения критерия и изменения времени работы
Сравнивались 2 метода решения, метод динамического программирования (ДП), который дает точное решение и предложенный эвристический метод (ЭМ), который дает приближенное решение. Сравниваются показатели «Отклонение критерия» и «Изменение времени работы» методов ДП и ЭМ. Результаты показывают (таб. 1 и рис. 1), что эвристический метод быстрее работает во всех случаях, разрыв во времени увеличивается с увеличением числа узлов сети, но при этом уменьшается точность полученных решений задачи.
Рецензенты:
Татур М.М., д.т.н., профессор, заведующий кафедрой электронных вычислительных машин, Белорусский государственный университет информатики и радиоэлектроники, г. Минск.
Садыхов Р.Х., д.т.н., профессор кафедры электронных вычислительных машин, Белорусский государственный университет информатики и радиоэлектроники, г. Минск.



