Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Математическое моделирование акустоэлектромагнитного метода (АЭМ) неразрушающего контроля (НК) композиционных материалов (КМ) и полимеров с применением частотно-импедансного физико-математического подхода позволяет решить большое количество научных задач и полней интерпретировать результаты измерений при оценке механических свойств КМ. Несомненным преимуществом физико-математического моделирования АЭМ является возможность оценки свойств КМ и параметров зондирующих излучений с точки зрения информационной достоверности НК АЭМ, чем это можно было бы выполнить в экспериментах. Недостатком моделирования в некоторых случаях является введение допущений и ограничений в исходные параметры и режимы из-за сложности применяемого для решения задачи математического аппарата или необходимости учета большого количества факторов, не оказывающих серьезного влияния на исследуемый процесс, но существенно усложняющий модель [10].

При математическом моделировании волновых механических и электромагнитных процессов в веществе, как правило, используется волновая теория [9].

В силу новизны рассматриваемой задачи, а также судя по современным литературным данным, в настоящее время нет четкого понимания и толкования физических основ акустоэлектромагнитного метода [3]. Поэтому в материалах этой работы возникает необходимость рассмотреть факторы, влияющие на параметры электромагнитного излучения от кристаллитов частиц сегнетокерамики клеевого слоя, стимулируемые акустическими волнами, а также рассмотреть связь этих факторов от прочности клеевого соединения и установить их функциональную зависимость. Лишь установив эти функциональные зависимости, можно обоснованно выбирать коррелирующие параметры, исключая большое бесполезное количество экспериментальной работы и вычислительных операций по распознаванию образов [3].

Анализ эмпирических результатов АЭМ [1,2,5,6] позволяет сделать заключение, что только процесс синфазного преобразования акустической энергии в электромагнитную кристаллитами частиц сегнетокерамики дает возможность оценить прочностные свойства клеевого соединения. Это становится возможным благодаря тому, что и адгезив, и частицы, введенные в него, одновременно испытывают на себе действие одних и тех же факторов [6].

Знание физических основ АЭМ позволяет: анализировать протекающие процессы в нем, находить границы его применения и выявлять причины корреляции параметров электромагнитного излучения с прочностными свойствами клеевого соединения. Кроме того, позволяет выявить не только реальные уровни корреляции и увеличить чувствительность АЭМ, но находить регрессионные соотношения, описывающие связь электромагнитного излучения АЭМ и адгезионной прочности КМ [1,2,5,6].

Таким образом, задачей настоящей работы является исследование частотной зависимости электромагнитного излучения от прочностных свойств клеевого соединения.

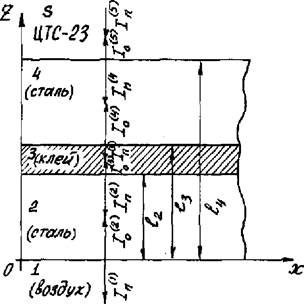
Рис.1. К вопросу о нахождении резонансных свойств трехслойной системы. интенсивность падающей упругой волны соответственно в 1-й, 2-й, 3-й, 4-й, 5-й средах, – толщина второго слоя, толщина второго слоя вместе с клеевым соединением, толщина композиционного трехслойного изделия

При реализации АЭМ в изделие или образец излучают широкополосные механические колебания [5]. При этом механические колебания разных частот взаимодействуют с образцом, усиливаются или ослабляются в зависимости от резонансных свойств КМ. В соответствии с теориями, излагаемыми в [4,7,9], в жестко связанных с большим коэффициентом затухания систе­мах резонансы возникают лишь на частоте системы и ее гармониках. Так как частицы сегнетодобавок имеют размеры (10-5–10-8 м) и соизмеримы или меньше длины акустических волн, лежащие в об­ласти сотен МГц, то они одинаково реагируют на частоты, лежащие в области резонансных свойств изделий. Этот факт позволяет счи­тать в области рассматриваемых частот КМ коэффициент электромехани­ческой связи активированного клеевого шва постоянным.

В общем случае все слои такой системы должны рассматриваться как элементы с распределенными параметрами [4]. Исключив из рассмот­рения площади поперечного сечения луча акустических колебаний, пе­рейдем к удельным величинам. Тогда определяющий резонансные свойства системы входной механичес­кий импеданс можно найти, решая систему волновых уравнений с соответствующими граничными условиями.

При дальнейшем рассмотрении, для упрощения математической модели будем считать, что композиционное изделие состоит из 3-х слоев. При­своим соответственно номера 5, 4, 3, 2 и 1 среде, из которой па­дает волна, слоям системы и среде, в которую проходит волна, это изображено на рис.1.

Система волновых уравнений, с помощью которых найдем вол­новой импеданс КМ, будет иметь вид:

где звуковой поток в й среде, координаты и время соответственно, плотность й среды, сжимаемость й среды, причем решение системы уравнений должно удовлетворять граничным условиям:

 (2)

где соответственно координаты границ от границы слоя 1 – 2. Решение системы дифференциальных уравнений (1) с учетом граничных условий (2) имеет вид волновых функций, характеризующих упругие волны в соответствующих слоях КМ:

 (3)

где амплитуда падающей упругой волны в й среде, амплитуда отраженной упругой волныв й среде, круговая частота упругих колебаний среды, волновое число й среды, скорость распространения упругих волн в й среде.

Зная, что импеданс определяется отношением давления к скорости смещения частиц среды [9], получим, решая систему (3), систему уравнений для давления упругих волн и скорости смещения частиц среды, выразив в соответствии с выражениями:

Таким образом, звуковое давление и скорость частиц в средах композиционного изделия будет иметь вид:

Решая систему (5) методом, описанным в [4], получим для входного импеданса трехслойной системы (при так как среда 1 и 5 – воздух, а среда 2 и 4 – сталь, на границе сталь – воздух происходит полное отражение упругой волны) выражение вида:

где импеданс, толщина слоя.

Модель уравнения (6) для трехслойной системы, у которой слой 4 и 2 имеют одинаковые акустические параметры, будет иметь вид:

где и плотность соответственно клеящего полимера с кристаллитами сегнетокерамики и склеиваемых деталей, и скорость распространения упругих волн соответственно в клеящем полимере с кристаллитами сегнетокерамики и склеиваемых деталях, резонансная частота трехслойного композиционного изделия.

Для произвольной, т.е. имеющей несопоставимые параметры, трехслойной композиционной системы решение уравнения (6) будет иметь вид:

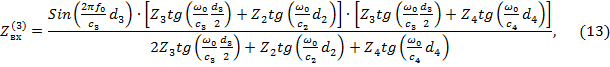
где соответственно толщины 2, 3 и 4-го слоев КМ. Решение уравнения (13) аналогично решению уравнения (7), но имеет более сложное решение и описывает большее количество резонансных частот. Для понимания АЭМ достаточно решения уравнения (7).

Найдем резонансные частоты композиционного материала, описанного уравнением (7), для этого представим это уравнение в виде.

где , ,

продифференцируем дважды выражение (9), получим второе уравнение, характеризующее процесс распространения акустических волн в нашей трехслойной системе, которое будет иметь вид:

Решая совместно уравнения (9) и (10), найдем значения тангенсов,

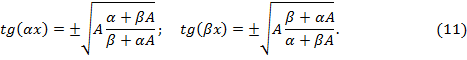
откуда получим, что наша композиционная система имеет восемь основных резонансных частот и 8n гармоник, которые описываются системой уравнений:

,,

,

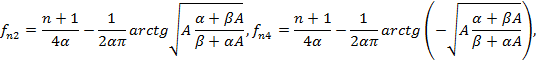
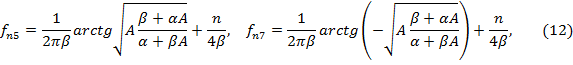
Рассмотрим модели композиционных материалов, отображающих: качественное изделие КМ №1, изделие с дефектом типа «пустота» КМ №2, изделие с дефектом типа «прижатый непроклей» КМ №3.

1. Композиционный материал № 1 состоит из двух стальных пластин (), качественно склеенных эпоксидным клеем с добавками кристаллитов сегнетокерамики (). КМ будет иметь характеристики уравнения (9):, , . Подставляя эти значения в систему (12), получим значения резонансных частот от основной до n гармоники, соответствующих нашему композиционному изделию. Изделие имеет восемь основных () резонансных частоты и бесконечное множество гармоник.

2. Композиционный материал № 2 состоит из двух стальных пластин имеет непроклеи толщиной заполненный воздухом, для которого . Вычислим параметры для уравнения (9) , , . Подставляя эти значения в выражение (12), получим значения восьми резонансных частот основных гармоник, соответствующих изделию при наличии таких дефектов в зоне контроля.

3. Рассмотрим КМ №3, состоящий из двух стальных пластин , имеющий прижатый непроклей с толщиной слоя а воздух и клей отсутствуют. Вычислим параметры для уравнения (9) , ,,. Подставляя эти значения в выражение (12), получим значения восьми резонансных частот основных гармоник упругих колебаний, соответствующих изделию при наличии такого дефекта в зоне контроля.

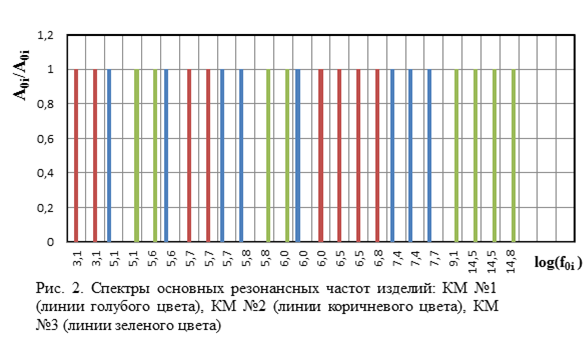
Вычисления сведем в таблицу, на основании которой построим диаграмму и проанализируем результаты. В первом столбце таблицы размещены номера резонансных основных частот спектра, вычисленных в порядке системы (12). Второй третий и четвертый столбец, соответственно резонансные частоты соответствующих изделий. Нижняя строка, вычисленная средняя частота спектров. Используя данные таблицы, построим диаграмму спектров. По оси абсцисс отложены десятичные логарифмы частот, по оси ординат приведенные амплитуды резонансных частот. На основании этой диаграммы сделаем выводы.

Таблица. Резонансные частоты, вычисленные для: КМ №1, КМ №2, КМ №3

Выводы

1. Из диаграммы следует, что КМ № 2, имеющий дефект типа «Пустоты», имеет резонансный спектр, сдвинутый в сторону меньших частот относительно спектра нормального КМ № 1, и уменьшает в 2,14 раза среднюю частоту спектра. КМ № 3, имеющий дефект типа «Прижатый непроклей», сдвигает резонансный спектр в сторону больших частот относительно спектра нормального КМ №1 и увеличивает в 15 раз среднюю частоту спектра.

2. Активированный ориентированными кристаллитами сегнетокерамики клеящий полимер выступает в композиционном изделии как датчик упругих волн и способен регистрировать резонансные частоты, присущие этому изделию. При этом активированное адгезионное соединение выявляет пустоты и прижатые непроклеи как в себе, так и в соседних не активированных адгезионных соединениях.

3. Полученные данные хорошо согласуются с данными акустического резонансного метода [8], дающего аналогичные экспериментальные результаты, но имеющего меньшую точность за счет присоединенных импедансов излучателя и приемника и соответственно большее количество основных резонансных частот.

Рецензенты:

Сидуленко О.А., д.т.н., с.н.с., директор «АНО «Научно-исследовательский институт интроскопии», г. Томск.

Каленский А.В., д.ф.-м..н., доцент, профессор кафедры химии твердого тела ФГБОУ ВПО «Кемеровский государственный университет» «КемГУ», г. Кемерово.