При построении вычислительного алгоритма для расчета течений с использованием неявных разностных схем возникает важная задача, связанная с решением системы линейных алгебраических уравнений (СЛАУ) большой размерности. В задачах моделирования несжимаемых течений с использованием метода SIMPLE вычислительный алгоритм строится на основе метода расщепления по физическим процессам, сводящегося к последовательному решению систем дифференциальных уравнений [2]. Выбор метода решения разностных уравнений оказывает существенное влияние на устойчивость вычислительного алгоритма и скорость сходимости итерационного процесса.
При решении задач вычислительной гидродинамики методом SIMPLE до 90% вычислительного времени приходится на решение СЛАУ, составленной относительно поправки давления. Данная матрица СЛАУ симметрична и не имеет строгого диагонального преобладания. Из мировой практики известно, что наиболее подходящим методом для решения таких СЛАУ является алгебраический многосеточный метод (AMG) [5], который существенно позволяет увеличить скорость сходимости и минимизировать затраты машинного времени и памяти. Кроме вышеуказанных свойств этого метода, он обеспечивает монотонную сходимость, что немаловажно, так как в методе SIMPLE нет смысла решать СЛАУ с высокой точностью – многократное повышение точности лишь незначительно сокращает общее число шагов решателя SIMPLE. Это дает преимущество на данных задачах перед, например, предобусловленным методом сопряженных градиентов (PCG), что показано на рисунке 1. На данном графике сравнивается сходимость алгебраического многосеточного метода, которому посвящена данная статья, и метода сопряженных градиентов с предобуславливателем Эйзенштата [4].
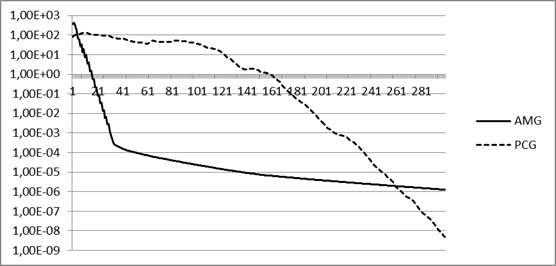
Рисунок 1. Сходимость методов решения СЛАУ.
В многосеточном методе обычный итерационный процесс комбинируется с коррекцией решения на последовательности грубых сеток. Рассмотрим систему уравнений:
. (1)
Оператор интерполяции P с грубой сетки H на подробную сетку h позволяет представить оператор 
на грубой сетке в виде
, (2)
где 
. Шаг коррекции решения имеет вид:
. (3)
Коррекция решения 
является точным решением уравнения
, (4)
где 
.
Таким образом, многосеточный метод, использующий схему коррекции решения, представляет собой следующую последовательность шагов.
1. Делается 
приближений решения на сетке h при помощи метода Зейделя (предварительное сглаживание).
2. Невязка 
проецируется на пространство 
, т.е. 
.
3. Находится приближенное решение на грубой сетке. Для этого рекурсивно делается 
циклов многосеточного метода.
4. Коррекция интерполируется на подробную сетку и производится коррекция решения на подробной сетке .
5. Делается 
приближений решения на подробной сетке для подавления ошибки интерполяции (заключительное сглаживание).
В зависимости от числа рекурсивных вызовов метода на каждом сеточном уровне выделяют различные типы циклов.
При 
имеет место быть V-цикл, а при 
– W-цикл (рис. 2).
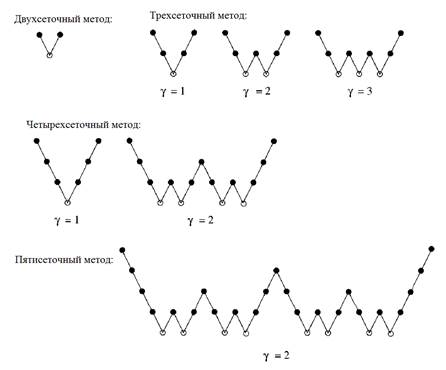
Рисунок 2. V- и W-циклы.
Если на каждом уровне рекурсивно сначала вызывать один W-цикл, а затем V-цикл, получим F-цикл (рис. 3).
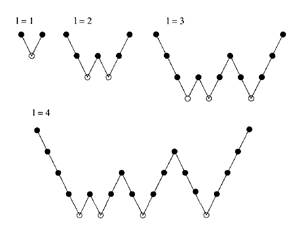
Рисунок 3. F-цикл.
В данной работе реализован агрегативный метод огрубления с постоянной интерполяцией [6]. Все переменные разделяются на агрегаты 
, где содержит все индексы i, соответствующие ячейкам, которые включены в агрегат k.
Построение оператора на грубой сетке производится при помощи соотношения:
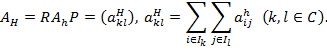(5)
Рассмотрим сетку, огрубление которой показано на рисунке 4.
Рисунок 4. Пример огрубления сетки.
Вычисление матрицы грубого уровня, в данном случае, будет происходить следующим образом:
.
Для хранения матрицы использован ячеечно-граневый формат. Отдельно хранятся диагональ D, верхнетреугольная U и нижнетреугольная L части матрицы. Соответственно, 
. Эти три массива являются одномерными. Массив, хранящий диагональ, индексируется номером соответствующей ячейки. Два других массива индексируются номерами граней, определяющих значения соответствующих коэффициентов. Упорядочение массивов представлено на рисунке 5.
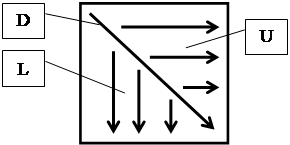
Рисунок 5. Расположение матрицы в памяти.
В данной работе в качестве сглаживателя используется метод Зейделя [1]:
, (6)
где N – число ячеек.
Но в данном представлении метода (6) возникают сложности при работе с матрицей в ячеечно-граневом формате, кроме того, доступ к данным осуществляется не по порядку, плохо используется кэш (рис. 5). Преобразовав данный алгоритм к виду (7), можно добиться строго последовательного доступа к элементам массивов хранения коэффициентов матрицы.
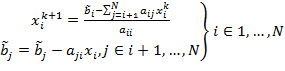, (7)
где 
– копия вектора b, подвергающаяся модификации в процессе работы алгоритма.
Распараллеливание организовано с помощью фиктивных ячеек. На рисунке 6 показана передача информации, возникающая при применении данного подхода.
Рисунок 6. Передача информации в фиктивные ячейки.
Огрубление происходит независимо на каждом процессе. Фиктивные ячейки огрубляются в соответствии с огрублением их действительных прообразов на соответствующих процессах. Таким образом, в процессе огрубления число связей между процессами уменьшается.
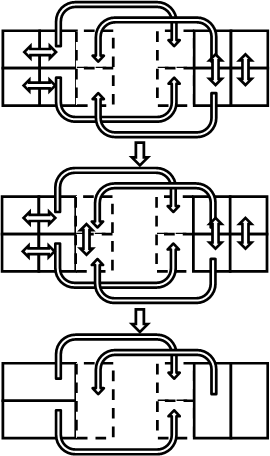
Рисунок 7. Огрубление ячеек в параллельном режиме.
Следует отметить, что данный подход к распараллеливанию огрубления порождает две проблемы. Во-первых, огрубление останавливается в случае, если на каждом процессе осталось по одной действительной ячейке. Во-вторых, на грубых уровнях, где размерность матриц невелика, время, затрачиваемое на межпроцессорные обмены, из-за латентности коммуникационной среды начинает многократно превосходить время, затрачиваемое на вычисления. Для решения данных проблем в рамках данной работы предложено выполнять сбор всех матриц небольшого размера на одном процессе, формировать из них глобальный уровень и продолжать огрубление и решение в последовательном режиме (рис. 8).
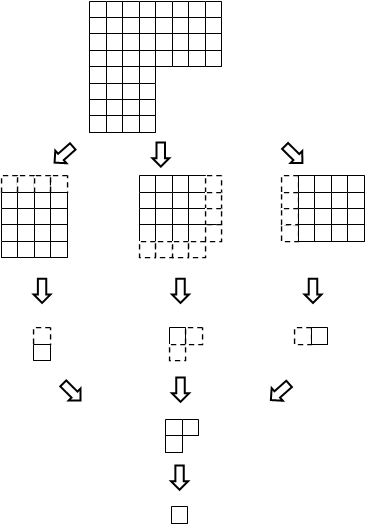
Рисунок 8. Глобальный уровень.
Алгебраический многосеточный метод был протестирован на нескольких задачах. СЛАУ давления в этих задачах решались многосеточным решателем, которому посвящена данная работа, и внешним алгебраическим многосеточным решателем BoomerAMG [3] с оптимизированными параметрами (Strong threshold = 0.25, Interpolation type: direct, Coarsen type: HMIS, Relax type: HSGS). Относительная точность в обоих случаях была равна 
, максимальное число циклов многосеточного метода – 30. Выполнялись 1000 шагов метода SIMPLE. Результаты вычислительного эксперимента задачи расчёта турбулентного обтекания потоком вязкого несжимаемого газа (воздуха) грузового автомобиля КАМАЗ (рис. 9) представлены в таблице 1, а задачи течения охлаждающей жидкости в монолитной головке рубашки охлаждения блока цилиндров двигателя автомобиля (рис. 10) – в таблице 2.
Рисунок 9. Задача расчёта турбулентного обтекания потоком вязкого несжимаемого газа грузового автомобиля КАМАЗ.
Таблица 1 – Результаты вычислительного эксперимента задачи расчёта турбулентного обтекания потоком вязкого несжимаемого газа грузового автомобиля КАМАЗ
|
Тип решателя |
Число процессов |
Время решения, секунд |
|
Внутренний многосеточный |
288 |
1198 |
|
Внешний многосеточный |
288 |
3418 |
Рисунок 10. Задача течения охлаждающей жидкости в монолитной головке рубашки охлаждения блока цилиндров двигателя автомобиля.
Таблица 2 – Результаты вычислительного эксперимента задачи течения охлаждающей жидкости в монолитной головке рубашки охлаждения блока цилиндров двигателя автомобиля
|
Тип решателя |
Число процессов |
Время решения, секунд |
|
Внутренний многосеточный |
96 |
218 |
|
Внешний многосеточный |
96 |
608 |
Таким образом, на модели памяти ЛОГОС был реализован алгебраический многосеточный метод. Тестирование метода на различных задачах показало его устойчивую работу и высокую скорость решения СЛАУ. Реализованный метод в составе программного комплекса ЛОГОС был передан на предприятия в сентябре 2012 г.
Рецензенты:
Щенников В.Н., д.ф.-м.н., профессор, заведующий кафедрой дифференциальных уравнений факультета математики и информационных технологий ФГБОУ ВПО «Мордовский государственный университет им. Н.П. Огарёва», г. Саранск.
Малыханов Ю.Б., д.ф.-м.н., профессор, профессор кафедры физики и методики обучения физике физико-математического факультета ФГБОУ ВПО «Мордовский государственный педагогический институт имени М.Е. Евсевьева», г. Саранск.