Введение
Известно, что распределение химических веществ на земной поверхности, в том числе в почве, может носить фрактальный характер [9, 10]. По результатам отбора проб на местности и данным результатов экологического мониторинга в работе [6] показано, что фрактальные модели могут успешно использоваться для изучения полей поверхностных загрязнений. В то же время вопрос чувствительности значения фрактальной размерности Df к тем или иным метеорологическим факторам (направление, скорость ветра и др.), физико-химическим характеристикам загрязняющих веществ (размер и плотность частиц, фазовый состав и др.), особенностям эмиссии (высота и интенсивность источника загрязнения, геометрическое расположение источников и др.) остается открытым. Поскольку отбор и анализ проб являются трудоемкими процедурами, а реальные природные условия не позволяют провести серию однозначно интерпретируемых экспериментов, на начальном этапе исследования целесообразно использовать поля загрязнений, рассчитанные по соответствующим моделям. Наиболее удобными в этом отношении являются имитационные модели клеточных автоматов (КА) [4]. Клеточные автоматы нашли устойчивое применение в качестве концептуальных и практических моделей пространственно-распределенных динамических систем, для которых физические системы являются первыми и наиболее важными прототипами (модели уравнения теплопроводности, волнового уравнения и др.). КА применяются для изучения коллективных явлений – упорядочения, хаоса, нарушения симметрии, фрактальности – в системах, состоящих из большого числа частиц, нелинейно взаимодействующих друг с другом [8].
Целью настоящей работы является определение чувствительности значения фрактальной размерности Df модельных полей поверхностных загрязнений к количеству и взаимному расположению источников загрязнения.
Имитационная модель формирования полей поверхностных загрязнений
Модель реализуется в вычислительной среде клеточных автоматов (КА) на трехмерной решетке. Управляющие правила КА модели формализуют явления эмиссии (выброса) загрязняющих веществ, их массопереноса и выпадения на подстилающую поверхность, а также явления вторичного массопереноса [2].
Независимость трудоемкости расчетов моделей клеточных автоматов от количества правил позволяет реализовать в одной численной модели комплекс физических процессов и естественно учитывать суперпозицию источников загрязнений, различающихся как по форме и интенсивности, так и по длительности выбросов [5]. Благодаря правилам локального взаимодействия соседних ячеек решетки, учитывается конечная скорость распространения примеси, задаются дискретные граничные условия любой сложности [8].
Все расчеты полей загрязнений в настоящей работе проведены с использованием автоматизированного комплекса для расчета полей поверхностных загрязнений EcoCALab [1], позволяющего моделировать полный жизненный цикл формирования полей поверхностных загрязнений [3].
В модельных расчетах использовались правила КА, описывающие следующие процессы:
- эмиссия загрязняющего вещества (мощность, количество и расположение источников загрязнения);
- массоперенос (ветровой перенос, турбулентная диффузия);
- выпадение загрязняющего вещества на подстилающую поверхность.
В каждой ячейке решетки КА задано значение концентрации загрязняющего вещества, величина которого на каждом цикле расчета изменяется по заранее заданным управляющим правилам КА с учетом значений концентраций в соседних ячейках. Результатом расчета является поле выпадения – совокупность значений концентраций в каждой ячейке самого нижнего слоя решетки, соответствующего подстилающей поверхности.
Модельное поле загрязнений (рис.1 а, б) от одного точечного источника получено при следующих условиях: площадь ячейки Sя = 100 м2, поле 2000 м на 2000 м и высотой атмосферы 1000 м, с постоянным коэффициентом диффузии Dдиф = 10 м2/с, постоянной скоростью седиментации vсед = 0,5 м/с, с постоянной вероятностью эмиссии pэм = 1,0, в отсутствие ветра vветра=0.
Значение фрактальной размерности Df поля рассчитано согласно фрактальной модели поверхностных загрязнений [7]. Основу расчета Df по этой модели составляет исследование зависимости массы загрязняющего вещества от занимаемой им площади при концентрации выше заданного уровня, построенной в дважды логарифмических координатах. Для расчета фрактальной размерности модельного поля загрязнений использовались значения концентрации выпадений в каждой ячейке нижнего слоя решетки.
Ячейки объединялись в группы с одинаковой концентрацией Ci, подсчитывалось количество ячеек Ni в каждой группе. Общая площадь всех ячеек Si, концентрация загрязняющего вещества в которых равна Ci, определяется как:
Si = Nя Sя (1)
Общая масса загрязняющего вещества Mi, находящегося в ячейках i-й группы:
Mi= Ci Si (2)
Для построения в соответствии с фрактальной моделью [7] зависимости Ln(∑Mi)~Ln(∑Si) необходимо подсчитать суммарную площадь ∑Si и суммарную массу ∑Mi для групп с концентрациями Ci и больше.
∑Si = Si +Si-1+ Si-2+…+ S1 (3)
∑Mi = Mi +Mi-1+ Mi-2+…+ M1 (4)
Два вектора значений площади ∑Si и массы ∑Mi позволяет построить требуемую зависимость Ln(∑Mi)~Ln(∑Si), рис.1,в, г. Наличие линейного участка кривой подтверждает справедливость фрактальной модели распределения загрязнений. Df равна удвоенному значению угла наклона этой зависимости [6]. Не всегда эта зависимость является линейной во всем диапазоне концентраций, поэтому появляется необходимость выделения на полученном графике линейного участка.
а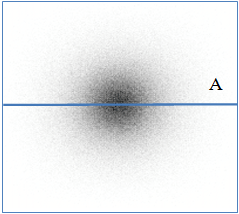 б
б 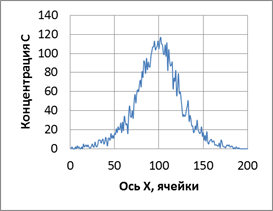
в 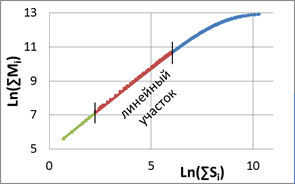 г
г 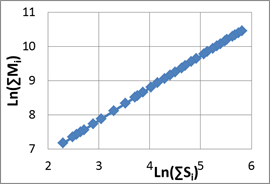
Рис.1 – а) вид сверху, поле загрязнений одного точечного источника; б) распределение концентраций загрязняющего вещества в сечении A; в) зависимость Ln(∑Mi)~Ln(∑Si) для полного диапазона значений концентрации; г) расчет фрактальной размерности по зависимости Ln(∑Mi)~Ln(∑Si), Df = 1,88±0,01
Зависимость значения фрактальной размерности от количества и взаимного расположения источников
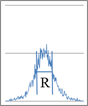
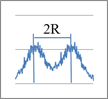
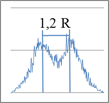
Были рассчитаны 2 серии полей загрязнений для 1, 2, 3, 4-х точечных источников, отличающихся расстоянием между источниками. Расстояние между «далеко» расположенными источниками составляло 2R ≈ 1 км (серия А), «близко» расположенными источниками – 1,2R ≈ 0,6 км (серия В), табл. Условия для каждого эксперимента серий А и В аналогичны условиям для единственного источника, изображенного на рис.1. На рис. 2 приведена итоговая зависимость значения фрактальной размерности Df от количества и взаимного расположения источников.
Таблица – Модельные поля поверхностных загрязнений
|
Nист Серия |
1 |
2 |
3 |
4 |
Расстояние* |
|
А |
|
|
|
|
|
|
B |
|
|
|
|
*Расстояние между источниками
Примечание. R – полная ширина на половине высоты сечения одного источника.
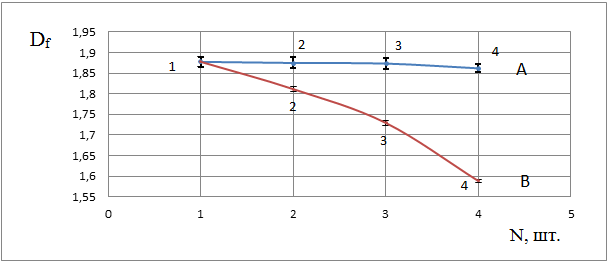
Рис.2 – Зависимость значения фрактальной размерности Df от количества источников N и расстояния между ними. Серия А – «далекое» расположение источников (2R ≈1 км), серия В – «близкое» (1,2R ≈ 0,6 км).
Видно, что значение Df значимо зависит от количества источников только при их относительно «близком» (серия В) расположении. Это объясняется тем, что при таком расположении имеет место взаимное наложение друг на друга полей загрязнений от разных источников, вклад каждого источника является нелинейным, что качественно меняет картину загрязнения. Значение Df изменяется от 1,88±0,01 (для 1 источника) до 1,591±0,003 (для 4-х источников).
В случае относительно «далекого» расположения источников (серия А) такое наложение отсутствует, их вклад является аддитивным, и качественных изменений поля загрязнения не наблюдается. Значения Df для 1, 2, 3, 4-х «далеко» расположенных точечных источников равны 1,86 и находятся в пределах погрешности расчета, составляющей ∆ ≈ 0,05.
Выводы
Значение фрактальной размерности, рассчитанное для модельных полей загрязнений, оказалось чувствительным к расстоянию между источниками и их количеству в случае, когда имеет место наложение полей загрязнений от различных источников друг на друга.
Таким образом, данный параметр является информативным для исследования полей поверхностных загрязнений. Для корректной интерпретации результатов измерений фрактальной размерности реальных полей загрязнений необходимо изучить чувствительность Df к метеорологическим факторам, физико-химическим характеристикам и др.
Работа была выполнена при частичной поддержке проекта ориентированных фундаментальных исследований УрО РАН "Арктика" - №12-2-3-010- АРКТИКА.
Рецензенты:
Максимов В.И., д.ф.-м.н., профессор, заведующий отделом дифференциальных уравнений ФГБУН Института математики и механики им. Н.Н.Красовского УрО РАН, г. Екатеринбург.
Вараксин А.Н., д.ф.-м.н., профессор, заведующий лабораторией математического моделирования в экологии и медицине ФГБУН Института промышленной экологии УрО РАН, г. Екатеринбург.