Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Введение

При численном решении многомерных уравнений Навье-Стокса требуется аппроксимировать с высоким порядком точности как конвективные, так и диффузионные члены.

В настоящей статье предлагается численный алгоритм решения уравнений диффузионного типа на основе разрывного метода Галёркина [4], который хорошо зарекомендовал себя для решения уравнений Навье-Стокса [5, 6, 8]. Численный алгоритм рассматривается на примере решения начально-краевой задачи для двумерного уравнения теплопроводности. В статье [2] были рассмотрены несколько численных схем, отличающиеся вычислениями на границе расчетной области. В этой работе рассматривается самый оптимальный с точки зрения точности и сходимости вариант. Было введено масштабирование базисных функций, что увеличивает устойчивость рассматриваемой численной схемы. Рассматриваемый алгоритм сравнивался с хорошо известным методом конечных объемов и хорошо зарекомендовавшим себя методом Галёркина с разрывными базисными функциями. На основе разработанного численного алгоритма находится решение ряда модельных задач.

Описание предлагаемого метода на основе разрывного метода Галёркина для уравнения теплопроводности.

Построение и исследование алгоритма метода решения уравнений диффузионного типа на основе разрывного метода Галёркина [4] проведем на примере двумерного уравнения теплопроводности:

(1)

с начальным условием

и граничным условием

при

где – коэффициент теплоемкости при постоянном объеме, – плотность, – коэффициент теплопроводности, – температура в точке в момент времени – плотность тепловых источников, – граница области расчета, – заданные функции. Область – произвольная односвязная. Для применения метода на основе разрывного метода Галёркина в области зададим множество точек содержащее внутренние и граничные точки области . На построим триангуляцию Делоне: Пусть содержит все узлы ; все треугольники имеют ненулевую площадь и пересекаются не более чем по образующим их вершинам или ребрам. В каждом из треугольников определим центр и середины сторон. В треугольнике с вершинами в точках центр определим как: Также примем в рассмотрение двойственную сетку, составленную из барицентрических объемов вокруг каждой из точек , образованных отрезками, соединяющими центры треугольников с серединами сторон (Рис. 1). Точка из будет являться центром соответствующей ей ячейки двойственной сетки.

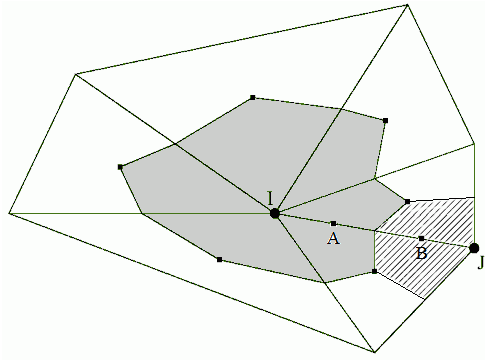
Рис. 1. Барицентрический объем вокруг вершины (серый цвет) и часть барицентрического объема вокруг вершины (заштрихован) и две квадратурные точки Гаусса ( и ) на ребре треугольника.

Для аппроксимации уравнения (1) с помощью разрывного метода Галёркина необходимо преобразовать его к системе дифференциальных уравнений в частных производных первого порядка. Для этого введем дополнительные переменные [5]: , .

Тогда уравнение (1) можно переписать в виде:

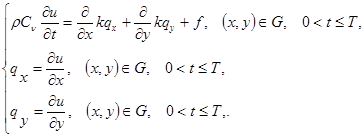(2)

На каждом треугольнике приближенное решение (2) будем искать в виде проекции на пространство полиномов степени 1 в базисе где – центр треугольника , – проекции треугольника на соответствующие оси.

На каждой ячейке двойственной сетки приближенное решение (2) будем искать в виде проекции на пространство полиномов степени 1 в базисе где – центр ячейки , – проекции ячейки двойственной сетки на соответствующие оси.

В каждой ячейке основной и двойственной сетки линейная комбинация базисных функций определяет решение в ячейке:

, ,

, , ,

, , ,

Определим коэффициенты разложения из условия ортогональности невязки всем пробным функциям на каждом треугольнике [6].

, (3)

Отсюда получаем систему для определения .

Определим коэффициенты разложения из условия ортогональности невязки всем пробным функциям на каждой ячейке двойственной сетки .

, , (4)

, , (5)

Отсюда получаем систему для определения .

Для вычисления интегралов будем использовать квадратурные формулы Гаусса необходимой точности.

Вычисление криволинейного интеграла первого рода по границе треугольника и ячейки двойственной сетки

В случае вычисления интеграла по некоторому отрезку , т.е. 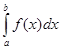, необходимо сделать замену вида: . В этом случае получаем:

.

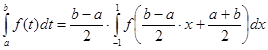В вычислениях мы использовали двухточечный шаблон. При этом значение и в точке берем из ячейки двойственной сетки вокруг вершины , а значение и в точке берем из ячейки двойственной сетки вокруг вершины (рисунок 1).

Вычисление двойного интеграла по треугольнику и ячейке

Двойной интеграл по ячейке двойственной сетки считаем как сумму двойных интегралов по треугольникам, из которых она состоит.

Следуя работе [7] возьмем три точки на каноническом треугольнике:

Значение интеграла по треугольнику с вершинами в точках равно

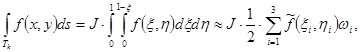
где – якобиан перехода к каноническому треугольнику, – значение подынтегральной функции в образах точек , , и в исходном треугольнике .

Описание тестовых задач и результаты расчетов

Были выполнены тестовые расчеты двух модельных задач. В качестве первой модельной задачи рассматривалась задача:

точное решение которой . Расчет производился до значения с одним и тем же числом Куранта.

Рис. 2. Пример «плохой» (слева) и «хорошей» (справа) сетки.

Результаты работы предлагаемого метода сравнивались с классическим разрывным методом Галёркина со стабилизационными добавками [8] и хорошо известным методом конечных элементов (FVM). В таблице 1 указано значение погрешности метода , где – площадь -го треугольника. В таблице представлены результаты работы предлагаемого метода (DG), классического разрывного метода Галёркина со стабилизационными добавками (CDG) и метода конечных элементов (FVM). Расчеты производились на «хорошей» сетке с минимальным углом треугольника и «плохой» сетке с произвольным углом треугольника (рисунок 2, «плохие» ячейки выделены серым цветом).

Таблица 1. Значения погрешности , полученные при решении задачи 1.

«Хорошая» сетка

«Плохая» сетка

В качестве второй модельной задачи рассматривалась задача [1]:

где . Решение сравнивалось с решением , полученным по чисто неявной разностной схеме с помощью метода расщепления [3] на подробной структурированной сетке. Расчет производился до значения с одним и тем же числом Куранта.

В таблице 2 указано значение погрешности метода , где – площадь -го треугольника. В таблице представлены результаты работы предлагаемого метода (DG), классического разрывного метода Галёркина со стабилизационными добавками (CDG) и метода конечных элементов (FVM).

Таблица 2. Значения погрешности , полученные при решении задачи 2.

«Хорошая» сетка

«Плохая» сетка

Выводы

Как видно из результатов расчетов, метод конечных объемов и классический метод Галёркина с разрывными базисными функциями сильно зависят от качества сетки, в то время как предлагаемый метод показывает работоспособность и на «хорошей», и на «плохой» сетках. Предлагаемый алгоритм не теряет работоспособности на «плохой» сетке за счет разнесенной сетки и вычисления градиентов на двойственной сетке, в то время как классический разрывный Галёркин и метод конечных объемов перестают работать из-за погрешности округления на сильно вытянутых ячейках, характерных для «плохой» сетки. При этом следует отметить, что предлагаемый метод на «хорошей» сетке не сильно отличается по точности от классического разрывного метода Галёркина со стабилизационными добавками.

Рецензенты:

Малыханов Ю.Б., д.ф.-м.н., профессор, профессор кафедры физики и методики обучения физике физико-математического факультета ФГБОУ ВПО «Мордовский государственный педагогический институт имени М.Е. Евсевьева», г. Саранск.

Чаткин М.Н., д.т.н., профессор, ректор ФГБОУ ДПО «Мордовский институт переподготовки кадров агробизнеса», г. Саранск, рп. Ялга.