На сегодняшний день в теории и практике высшей школы, реализующей Федеральный государственный образовательный стандарт, наиболее сложными являются вопросы диагностики сформированности компетенций как в целом – «на выходе» выпускника, так и после изучения дисциплин, профессиональных модулей, междисциплинарных курсов. Дискуссионными, требующими глубоких исследований являются вопросы о критериях и механизмах объективной динамической оценки уровня сформированности компетенций по результатам педагогических измерений на особых контрольно-измерительных материалах, содержание которых является главным в компетентностном подходе.
В этом контексте, на наш взгляд, заслуживает внимания методика использования системы критериальных компетентностно-ориентированных задач для диагностики уровня сформированности компетенций как после освоения учебной дисциплины, так и на завершающем этапе аттестации выпускника, разработанная М.В. Шингаревой [7].
Однако в рамках нашего исследования нами был разработан математический инструментарий, позволяющий определить зависимость вероятности достижения необходимого условного уровня обученности от времени для создания условий их мобильности на различных ступенях профессионального образования, в основу которого легла модель, предложенная Ириной Владимировной Самойло, для управления целенаправленным профессиональным выбором и последующим обучением различным дисциплинам с целью обеспечения компетенций, как на базовом уровне, так и на уровне профессиональной подготовки студентов вуза.
Различные исследователи предлагают использовать в качестве дидактических единиц диагностики следующие составляющие: оперативная единица деятельности (А.И. Галактионов, В.Н. Янушкин), типовая функциональная единица деятельности (А.И. Губинский), действия или операции (А. Н. Леонтьев), задачи деятельности (виды деятельности), адекватные им (Н.Ф. Талызина), учебный элемент (В.П. Беспалько), операторы целенаправленной деятельности при моделировании деятельности организационно-технических систем (Н.И. Буренин, Е.С.Кветковский), а также типовые единицы деятельности (ТЕД) (А.П. Свиридов), которые выделяются в учебной дисциплине (или в деятельности) в качестве элементарных составляющих.
Для создания математического инструментария, позволяющего производить диагностику сформированности компетенций, могут применяться методы математического моделирования, позволяющие описывать систему в компактной форме, используя для этого абстрактно-символическую форму записи. Однако необходимо учитывать, что при использовании математических методов возникает потребность в применении соответствующих средств автоматизации.
При разработке оценочного механизма учитывается тот факт, что «процесс обучения и управление знаниями вследствие присутствия человеческого фактора можно отнести к классу стохастических процессов[1] (при определенных условиях)», который можно рассматривать «как полумарковские процессы[2], вероятность перехода, при которых из одного состояния в другое зависит как от этого состояния, так и от состояния, в которое будет осуществлен следующий переход» [2]. Непрерывный процесс обучения при этом можно рассматривать в виде так называемых «графов перехода» из одного состояния знаний в другое в некотором интервале времени.
При построении математического инструментария необходимо учитывать, что каждый человек в силу развития своих способностей способен запоминать только определенное количество информации, при этом какая-то часть ее будет потеряна, вследствие развития памяти. Однако вся получаемая информация может служить источником для новых знаний.
Многочисленными теоретическими и эмпирическими исследованиями закономерностей формирования навыков, научения как процесса обучения в целом занимались Р. Аткинсон, Л. Брайен и Р. Вудвортс, В.П. Беспалько, Р. Буш и Ф. Мостеллер, В.Ф. Венда, А.М. Новиков, Д.А. Новиков, А.Б. Коган, Н.П. Наумов, В.Г. Режабек и О.Г. Чораян, И.И. Нурминский и Н.К. Гладышева, В.Ф. Присняков и Л.М. Приснякова, др.
Для оценки количества получаемой информации введем понятие «шаг обучения», под которым будем подразумевать «период времени между занятиями» [2].
Рассмотрим группу студентов общим количеством N, каждого обучающегося условно обозначим через in. Пусть этот i – обучающийся должен достигнуть состояния обученности Li, который складывается из объема знаний по данному предмету (Li = Qi, который Qi= Q1 + Q2 + Q3 +… Qn) – сумма всех зачетных единиц, которые должен иметь/знать i – обучающийся к концу изучения учебного элемента, субмодуля, модуля (рис. 11).
Отметим, что если в учебной группе всего N обучающихся, то «каждый из них должен достигнуть какого-либо состояния обученности L1, L2, L3, …, Li, …, Ln и эти состояния могут быть либо различными, либо одинаковыми (например, L), что определяется целями обучения» [2]. Иными словами:
1-й обучаемый может достигнуть уровня обученности L1 = Q1= Q1 + Q2 + Q3 +… Qn;
2-й обучаемый может достигнуть уровня обученности L2 = Q2= Q1 + Q2 + Q3 + Q4 … Qn; и т.д.
В начальный период времени, когда дисциплина только начинает изучаться для каждого обучающегося объем знаний, измеряемый в трудоемкости, равен Q0, а значит Ln= Q0, переход от одного учебного элемента к другому осуществляется со временем T0 (шаг обучения – период времени между учебными элементами).
Учитывая тот факт, что не все студенты постоянно посещают занятия, мы считаем, что это время отводится на самоподготовку (интерактивные методы обучения и т.д.), а, следовательно, периодичность посещения студентами группы можно считать относительно одинаковой (усредненный показатель). Кроме того, изученный материал усваивается у различных групп людей по-разному, вводим понятие «интенсивность потоков учебного материала или забывания» (λ, λi), которая показывает «какая часть знаний, умений и навыков теряется в единицу времени» и «интенсивность усвоения или обработки знаний» (μ, μi), которая показывает «какая часть знаний, умений и навыков усваивается в единицу времени» [2].
На основании вышесказанного считаем, что за один шаг обучения обучающийся усваивает Q – информации, которая характеризуется интенсивность усвоения μ и забывания λ за один шаг обучения T0.
После каждого шага обучающийся переходит в одно из k–возможных состояний в зависимости от количества усваиваемой учебной информации (УЭ* – учебный элемент) в данный момент времени (оно может быть от 0 до Lmax=Qmax).
Введем понятие вероятности нахождения состояния обучаемого (Р) в том или ином значении. Схематически процесс перехода, представлен на рис.
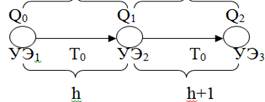
Рис. 1 Процесс перехода от одного учебного элемента к другому
После нескольких шагов обучения h (h=T0+T0+…+T0n) получаем следующие результаты на шаге h+1: РQ-μ.h – вероятность обладания уровнем знаний (Q-μ), при этом РQh – уровень знаний, равный необходимому объему знаний; РQ+λ.h– вероятность обладания уровнем знаний (Q+λ).
Получаем следующую математическую зависимость:
PQ,h+1= PQ-μ,h+PQ+λh- PQ,h (1)
Введем t=h·T0, где t – время процесса обучения, h – номер шага, T0 –длительность одного шага. Переходя от h к t, разложим уравнение (1) в ряд
Тейлора и, учитывая в правой и левой части полученного уравнения не более, чем вторые производные, получим:
![]() (2)
(2)
Разложив данное уравнение на составные части, получим следующую зависимость:
![]() – показывает общее изменение обученности во времени;
– показывает общее изменение обученности во времени;
![]() – показывает, что знания структурируются и сами становятся источником дополнительных знаний;
– показывает, что знания структурируются и сами становятся источником дополнительных знаний;
![]() – описывает упорядоченный переход либо в состояние, когда знания увеличиваются (μ›λ), либо когда уменьшаются (μ‹λ);
– описывает упорядоченный переход либо в состояние, когда знания увеличиваются (μ›λ), либо когда уменьшаются (μ‹λ);
![]() – описывает случайное изменение степени обученности.
– описывает случайное изменение степени обученности.
Далее вводится значение «плотность вероятности» (p(Q,t)) с целью получения граничной задачи (поскольку процесс считается непрерывным), решение которой и будет описывать процесс обучения.
Первым ограничением считаем, что когда уровень обученности будет равен объему получаемой информации, при расчете вероятности данный процесс может быть закончен, однако при p(Q,t)Q=L = 0.
Вторым ограничением считаем, что если уровень обученности не достигнут, а, следовательно, процесс усвоения равен 0, вводим данное ограничение с целью его недопущения p(Q,t)Q=0 = 0.
Считаем, что показатели интенсивности усвоения и забывания (ввиду введения ограничений) не зависят от объема информации. Тогда получаем следующие показатели: ![]() ;
; ![]() , подставим полученные значения в формулу 2 и получим следующую зависимость:
, подставим полученные значения в формулу 2 и получим следующую зависимость:
![]() (3)
(3)
Используя методы операционного исчисления для плотности вероятности ρ1(Q,t) и ρ2(Q,t) обнаружения состояния обученности i- обучаемого, в одном из значений на отрезке от 0 до L можно получить следующие уравнения:
- при условии Q›Q0
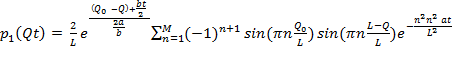 (4)
(4)
- при условии Q≤Q0
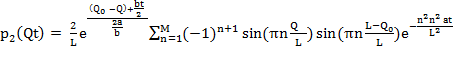 (5)
(5)
С точки зрения практики λ>μ представляет наибольший интерес для процесса обучения, знания накапливаются. Если вычислить интеграл P(L,t):
![]() (6)
(6)
то функция P(L,t) будет задавать вероятность того, что состояние обученности к моменту времени t будет находиться на отрезке от 0 до L, т.е. порог необходимой обученности L не будет достигнут.
Соответственно, вероятность Qi(t) того, что необходимый порог L окажется к моменту времени t достигнутым, можно определить следующим образом:
![]() (7)
(7)
График зависимости ![]() от времени (рис. 2) показывает, что первоначально уровень обученности не изменяется со временем, что свидетельствует о том, что получаемые знания не складываются в цельную структурированную картину о дисциплине. Далее наблюдается, постепенный рост степени обученности, а к концу освоения дисциплины у двадцати пяти процентов студентов этот показатель достигает максимального значения.
от времени (рис. 2) показывает, что первоначально уровень обученности не изменяется со временем, что свидетельствует о том, что получаемые знания не складываются в цельную структурированную картину о дисциплине. Далее наблюдается, постепенный рост степени обученности, а к концу освоения дисциплины у двадцати пяти процентов студентов этот показатель достигает максимального значения.
«Вероятность достижения обучающимися необходимого уровня обученности напрямую отражает долю изученного им материала, а также оценку, которую он может получить при проверке. Если критерием отличной оценки является доля изученного материала от 0,85 и выше, то критерием оценки «хорошо» является доля изучения материала от 0,65 до 0,85, а оценка «удовлетворительно» – от 0.65 до 0.45 и т.д.» [2].
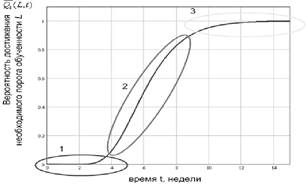
Рис. 2 Зависимость вероятности (Qi(t)) достижения необходимого условного уровня обученности L от времени
Таким образом, использование методов математического моделирования позволяет проанализировать динамику процессов формирования профессиональных компетенций средствами учебной дисциплины и определить вероятность достижения требуемого уровня обученности, в зависимости от индивидуальных возможностей каждого студента.
При переходе на следующий уровень профессионального образования в системе непрерывной профессиональной подготовки происходит сокращение сроков обучения за счет уменьшения объема изучаемой дисциплины, этот процесс также можно описать с помощью математической зависимости. В коллективной работе [5] учеными предложено следующее математическое уравнение:
![]() (8)
(8)
где Q1 – конечный объем знаний.
Оценку уровня обученности можно производить по количеству и сложности решаемых задач (некоторые источники предлагают данный показатель рассчитывать по количеству вопросов в тестах).
Показатель λ – интенсивность забывания, экспериментально получен И.В. Самойло и составляет λ=25*10-6![]()
После окончания колледжа студенты осваивают программу высшего образования за три года, в связи с этим уменьшается количество учебных часов, а, следовательно, уменьшается и значение передаваемого объема обученности по сравнению со студентами, изучающими данный курс в пятилетний срок.
Для получения более точной оценки необходимо учитывать остаточный объём знаний, умений, навыков, накопленных студентами при получении среднего специального образования. Это возможно при использовании специальной математической программы, описываемой выше.
Кроме того, данные значения можно определить, считая и интенсивность получения знаний, и забывания соответственно у студентов трех лет и пяти одинаковыми, не забывая при этом, что объем знаний у студентов полной программы обучения, только начинающих изучать данную дисциплину равен нулю.
Получаем первоначальный объем знаний у студентов сокращенной программы обучения, приравнивая остаточные знания к максимальному объему, передаваемых знаний:
![]() (9)
(9)
где Q1 – максимальный объем передаваемых знаний;
t5 – длительность полной программы обучения;
t3 – длительность сокращенной программы обучения.
Полученное выражение может быть использовано для определения соотношения в количестве часов планируемой учебной нагрузки для сокращенной и полной программы обучения.
Таким образом, объём начальных знаний Qос является эффективным инструментом для уменьшения времени обучения. Для специальной дисциплины это могут быть понятия, усвоенные при изучении других дисциплин, но забытые. Поэтому чем ранее забытая информация будет восстановлена для изучения нового материала, тем прочнее пройденный материал усваивается и закрепляется на основе создания ассоциативных связей в понимании обучаемого [4].
Из общей теории восстановления знаний (А.П. Свиридов, О.А. Бондин) известно, что время восстановления, как правило, гораздо меньше, чем время изучения и забывания («мгновенное» восстановление). Поэтому применение в начале занятий «восстановления» пройденного материала может дать существенный положительный результат. Использование расчетов степени обученности возможно при правильном построении учебной дисциплины, которая отвечала бы не только запросам инновационного развития, иными словами, была бы компетентно-ориентированной, но также имела бы четкую структуру, которую можно было подвергнуть математическому анализу.
Однако с учетом научной и практической новизны, сложности и многоаспектности проблемы диагностики процесса и результата формирования компетенций в условиях вуза, вышеназванные методики можно рассматривать лишь в качестве первого приближения к оптимальному решению этой проблемы. Определенную долю в ее решении может внести и использование модульной технологии построения структуры содержания учебных дисциплин, методики их освоения и контроля результатов обучения студентов.
Рецензенты:
Силайчев П.А., д.п.н., профессор, декан факультета заочного образования ФГБОУ ВПО «МГАУ им. В.П. Горячкина» г. Москва.
Степанов С.А., д.п.н., профессор, президент НОУ ВПО «Академия МНЭПУ» г. Москва.
[1] Стохастический процесс большинство источников трактуют как случайная функция в зависимости от некоторых параметров времени или координат.
[2] Цепь Маркова — последовательность случайных событий с конечным или счётным числом исходов, характеризующаяся тем свойством, что, говоря нестрого, при фиксированном настоящем будущее независимо от прошлого. Отличие полумарковского процесса динамики знаний от однородных цепей Маркова с непрерывным временем тем, что распределения времени пребывания в различных состояниях не экспоненциально.
* УЭ1, УЭ2, УЭ3 – учебные элементы, дидактически завершенные единицы в структуре содержания учебной дисциплины, по объему примерно равные вопросам изучения темы



