Введение
Высокий расход энергии на электролизерах с обожженными анодами (ОА) (13.0–14.5 кВт*ч/т Al) заставляет искать пути его снижения. Как известно [7; 8], удельный расход электроэнергии W определяется соотношением
, (1)
где U – напряжение на электролизере (В);
k – электрохимический эквивалент алюминия (г/А*ч);
η – выход по току (доли единицы).
Ясно, что следует снижать напряжение и/или увеличивать выход по току.
Написано множество книг и статей [7-9], в которых анализируется вклад той или иной составляющей в величину напряжения U, представляемого в виде:
, (2)
где Eр - равновесная ЭДС цепи
Al | Al2O3 | CO2, C; (3)
- сумма анодных перенапряжений;
- сумма катодных перенапряжений;
- падение напряжения в электролите;
- падение напряжения в аноде;
- падение напряжения в пузырьковом слое под анодом;
- падение напряжения в теле катода;
- средняя добавка к U за счет анодных эффектов;
- падение напряжения в ошиновке;
U – величина напряжения изменяется в пределах 3.7–4.8 В.
Что касается выхода по току, то количество книг и статей [9], в которых анализируется зависимость выхода по току от параметров электролиза, ничуть не меньше, а число параметров даже больше, поскольку потери металла (1-η) зависят от сложных условий электротепломассопереноса в общем процессе электролиза.
Несложные вычисления и простые инженерные соображения, основанные на анализе соотношения (1), показывают, что одним из путей снижения W, которому следуют многие компании мира, является уменьшение напряжения, и в частности величин 
, 
, 
. Среди указанных составляющих самой значимой является , которую в первом приближении можно оценить по уравнению
, (4)
где i – средняя плотность тока (А/м2);
l – межэлектродное расстояние (м);
ρ – удельное электрическое сопротивление (Ом*м).
Следует отметить, что в принципе естественно использовать способы уменьшения за счет снижения каждого из сомножителей в формуле (4).
Путь снижения межэлектродного расстояния очень привлекателен и может быть использован. Одной из его реализаций является размещение в межэлектродном пространстве дополнительных проводников (электродов) с величиной электрического сопротивления много меньшей, чем у электролита [5]. Форма, размер и материалы этих проводников могут быть различны, и для того чтобы определить их влияние на снижение величины , необходимо проведение экспериментов для анализа изменения распределений электрических полей в электролизере при различных геометрических размерах, форме и способах размещения дополнительных электродов. Ввиду сложности и высокой стоимости натурных и модельных физических экспериментов на первом этапе исследований целесообразно проводить вычислительные эксперименты на основе компьютерного моделирования электрических полей.
Компьютерное моделирование
Моделирование работы электролизера основывается на численном решении задач изменения, распределения и взаимодействия электромагнитных, тепловых, магнитогидродинамических полей и электрохимических процессов. Математическое моделирование и расчет взаимодействующих физических и химических процессов, с учетом конструктивных особенностей электролизера, представляет сложную проблему [1-3; 6]. При численном моделировании таких процессов в вычислительных технологиях для решения общей задачи эффективно применяются методы расщепления [4] по физическими процессам, которые рассчитываются последовательно по этапам для малых интервалов времени с учетом характерных скоростей изменения и последующими итерациями, учитывающими эффекты взаимодействия. Непосредственные оценки по энергетическому вкладу и скоростям изменения параметров приводят к необходимости в первую очередь проводить расчет распределения электрических полей при изменении геометрических параметров электролизера. Полученные решения могут быть использованы как первое приближение с последующим уточнением базового решения с учетом других факторов.
Для проведения компьютерного моделирования установившегося поля в вертикальном сечении электролизера рассматривается двухмерная краевая задача электростатики для кусочно-неоднородной среды Ω в координатах (y, z), где y – горизонтальная и z – вертикальная координаты.
На рис. 1 и 2, показан вид фрагментов вертикальных сечений электролизера без вставок и с двумя углеродными вставками соответственно. Геометрические размеры в миллиметрах приведены на рисунках.
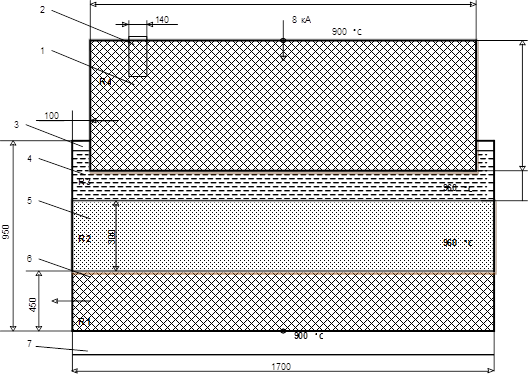
Рис. 1. Вертикальное сечение фрагмента электролизера без вставок: 1 – анод, 2 - стальные ниппели, 3 – глиноземная корка, 4 – электролит, 5 – жидкий алюминий, 6 – катод, 7 – блюмс.
Приведенные ниже результаты расчета основаны на сопоставлении численных решений о распределении электрических потенциалов φ(y, z) для разных вариантов положения вставок.
Для однородных сред потенциал φ удовлетворяет уравнению Лапласа, для неоднородных сред с гладко изменяющейся по координатам электропроводностью σ(y, z), которая в первом приближении полагается не зависящей от температуры среды, распределение потенциала φ описывается эллиптическим дифференциальным уравнением вида
div(σ(y,z)gradφ) = -f(y,z), (5)
где f(y, z) – удельная мощность источников (стоков) распределенных электрических зарядов. В рассматриваемой далее постановке задачи плотность распределенных электрических зарядов пренебрежимо мала и полагается нулевой.
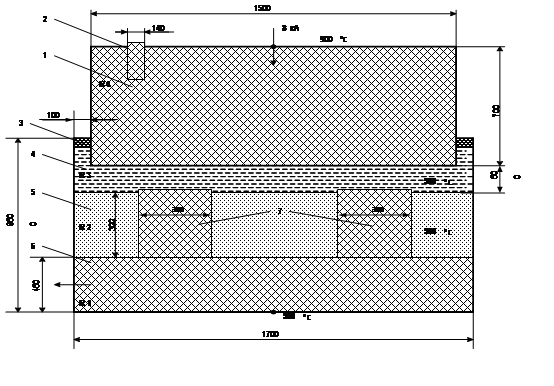
Рис. 2. Вертикальное сечение фрагмента электролизера с углеродными вставками: 1 – анод, 2 - стальные ниппели, 3 – глиноземная корка, 4 – электролит, 5 – жидкий алюминий, 6 – катод, 7 - углеродные вставки, 8 – блюмс.
Особенность рассматриваемой в данной работе постановки задачи состоит в том, что электропроводность σ(y, z) является разрывной функцией координат (y, z) по границам кусочно-неоднородного сечения электролизера (рис. 1, 2). Поэтому, чтобы не решать задачу для каждого однородного слоя или подобластей, с необходимостью в дальнейшем удовлетворения сложным смешанным граничным условиям Неймана – Дирихле на границах сопряжения областей, целесообразно использовать вместо дифференциальной постановки (5) интегральную формулировку задачи для всей области Ω или, как говорят, формулировку задачи в слабой форме [4; 10]. Интегральная формулировка задачи является удобным математическим приемом для возможности проведения расчетов в области Ω с разрывной функцией электропроводности σ(y, z) и какой-либо специальной физической интерпретации не имеет. Умножая правую и левую часть уравнения (5) на произвольную кусочно-гладкую пробную функцию 
и интегрируя по области Ω, получим
= 
. (6)
После применения интегральной формулы Грина соотношение (6) преобразуется к виду
(7)
Интеграл по границе области Ω преобразуется в соответствии с заданными граничными условиями общего вида 
, которые в предельном случае могут быть представлены как условия Неймана или Дирихле. Тогда соотношение (7) принимает вид
. (8)
Требуемое интегральное соотношение далее представляется в форме
(
. (9)
Соотношение (9) должно выполняться для любой пробной функции и представляет собой интегральную формулировку исходной задачи (5).
За счет проведенных интегральных преобразований в математической формулировке задачи в слабой форме (9) снижается требование на гладкость функции электропроводности σ(y, z), которая может являться разрывной функцией координат (y, z) на границах кусочно-неоднородной расчетной области Ω.
Далее в расчетной методике проводится дискретизация расчетной области Ω на конечные элементы. Совокупность приведенных процедур и лежит в основе построения метода конечных элементов (МКЭ) [10], который является более универсальным и продуктивным для численного решения подобных задач по сравнению с традиционно применяемыми конечно-разностными методами [1-3; 6].
Представленные ниже результаты компьютерного моделирования получены на базе использования среды MATLAB и математического пакета расширений Partial Differential Equation (PDE) Toolbox [10], в котором программно реализован МКЭ для аналогичных задач с автоматическим разбиением расчетной области на треугольные конечные элементы.
При проведении расчетов были использованы следующие параметры электропроводности 1/[Ом*м]: для анодного углерода 0.0384615*106, для стальных ниппелей и блюмсов 1.0*106, для электролита 0.02134*104, для жидкого алюминия 3.6036036*106, для катодного углерода и углеродных вставок 0.04* 106.
На вертикальных внешних границах расчетной области Ω задавалось условие 
(отсутствие тока в направлении, нормальном к границе). В нижней части катода, с учетом блюмсов, задавалось граничное условие 
, в правом выходном вертикальном сечении блюмса полагалось φ=0. На свободной поверхности горизонтальных участков (рис. 1, 2) задавалось условие 
. Для трех стальных ниппелей шириной по 150 мм и входной плотностью тока 26,666 кА/м2 задавалось эквивалентное равномерное распределение плотности тока на поверхности анода величиной 8 кА/м2.
На рис. 3 и 4 представлены результаты расчета распределения электрического потенциала φ и векторного поля плотности электрического тока 
в области Ω, что соответствует геометрии рис. 1 с учетом стального блюмса в нижней части катода.
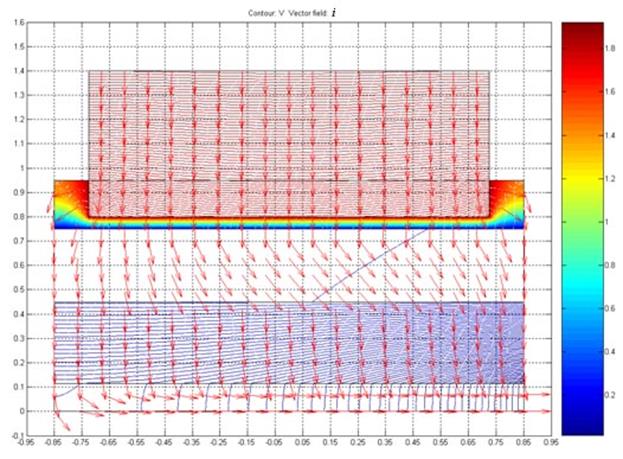
Рис. 3. Распределение нормированного векторного поля плотности электрического тока 
в вертикальном сечении электролизера и изолинии электрического потенциала ( 
- обозначает норму вектора, которая соответствует величине плотности электрического тока).
На рис. 4 представлены результаты расчета распределения электрического потенциала φ и векторного поля плотности электрического тока в области Ω с четырьмя углеродными вставками под анодом. При этом высота вставок над поверхностью жидкого алюминия составляет 25 мм c расстоянием между вставками 50 мм.
Приведенные расчеты сделаны для конечно-элементных сеток, дробление которых уже не приводит к каким-либо качественным и количественным изменениям численных результатов. Таким образом, установлена стабилизация численных решений.
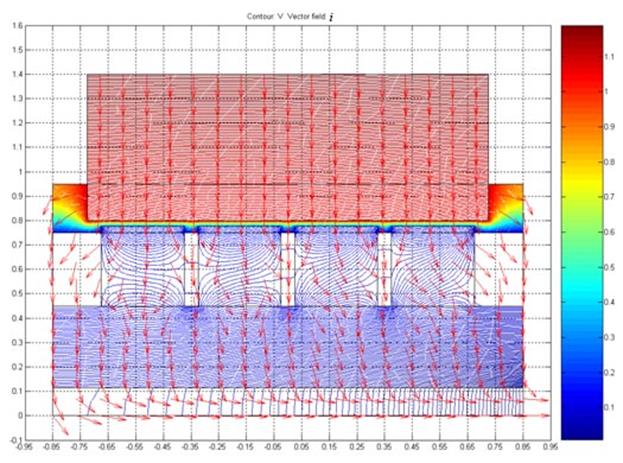
Рис. 4. Распределение нормированного векторного поля плотности электрического тока и изолинии распределения электрического потенциала в вертикальном сечении электролизера с углеродными вставками. Длина стрелок характеризует его интенсивность, при использовании четырех углеродных вставок с высотой 25 мм над поверхностью жидкого алюминия; шкала изменения электрического потенциала от 0 до 1.2 В. Блюмс находится в нижней части катода.
Заключение
Результаты проведенных расчетов для предложенных новых инженерных решений показывают, что при использовании углеродных вставок может быть достигнута значительная экономия электроэнергии за счет снижения рабочего напряжения на 0.8 В и вставки по патенту [5] следует рекомендовать к испытаниям. При среднем напряжении на алюминиевом электролизере 4.5 В снижение рабочего напряжения может составлять (0.8/4.5)*100% = 18%. Так как доля электроэнергии в структуре себестоимости производства 1 т алюминия составляет от 25 до 50%, то, например, при 30%-ной доле электроэнергии, при цене алюминия 2000 USD/тAl на заводе производительностью 1 млн тAl/год экономия может составить 0.18*(0.30*2000[USD/тAl]*1[млн тAl/год]) = 108 млн USD/год.
Рецензенты:
Пашков Г.Л., д.т.н., профессор, Федеральное государственное бюджетное учреждение науки «Институт химии и химической технологии» Сибирского отделения РАН (ИХХТ СО РАН), г. Красноярск.
Шепелев И.И., д.т.н., директор, Научно-исследовательская организация общество с ограниченной ответственностью «ЭКО-Инжиниринг» (НИО ООО «ЭКО-Инжиниринг»), г.Ачинск.