Введение
Одной из тенденций развития информационно-измерительной техники является переход от прямых методов измерения к косвенным и совокупным. при этом основная тяжесть в решении проблем переносится с аналоговых методов обработки измерительной информации на цифровые. Такой переход позволяет исключить из состава автоматизированных систем сложные и дорогостоящие аналоговые измерительные преобразователи.
Применение цифровых методов делает также возможным использование персонального компьютера, оснащенного стандартным АЦП в качестве универсальной измерительной станции, способной совместить процессы получения и обработки измерительной информации [2]. Такая станция может заменить целый ряд универсальных измерительных приборов, которые часто называют виртуальным прибором. Процесс измерения, который представляет собой оцифровку электрического напряжения и обработку по определенным алгоритмам полученных значений.
Постановка задачи. Во многих областях науки и техники перед исследователем возникает задача, как на основе данных, полученных на конечном интервале времени, сформировать максимально достоверное представление об основных характеристиках исходного сигнала. Развитие цифровой вычислительной техники значительно расширило сферы применения численных методов к оценке параметров сигнала.
Наиболее распространенные и простые в реализации методы спектрального оценивания, такие как БПФ и подход Блекмана-Тьюки, не дают необходимой точности, особенно при обработке зашумленных сигналов [5]. Исследования метода быстрого преобразования Фурье показывают, что погрешность определения амплитуды и частоты зашумленного гармонического сигнала составляет 1.5-2% [1]. Подход, часто называемый оценкой СПМ Блэкмана–Тьюки, имеет плохое разрешение даже для слабозашумленных сигналов [4]. Поэтому для определения параметров сигналов в условиях действия шумов и помех с высокой точностью необходимо использовать методы, которые лишены или хотя бы менее подвержены этим недостаткам.
К одним из таких методов оценивания параметров сигнала принадлежит метод разложения на собственные числа, который основан на анализе собственных значений автокорреляционной матрицы или одной из матриц данных. Этот метод обеспечивает лучшие характеристики разрешения и оценивания параметров, чем другие параметрические методы, особенно при низких отношениях сигнал/шум, когда эти методы не в состоянии различить близкие по частоте синусоиды или другие узкополосные спектральные компоненты [3].
Метод разложения автокорреляционной матрицы сигнала на собственные числа наилучшим образом соответствует задаче измерения параметров электрических сигналов в шумах на основании того факта, что при анализе собственных значений автокорреляционной матрицы происходит разделение информации на два векторных подпространства – подпространство сигнала и подпространство шума.
Автокорреляционная последовательность (АКП), состоящая из М комплексных синусоид описывается как
где Pj — мощность i-й синусоиды, а 
— дисперсия белого шума.
Тёплицева автокорреляционная (р+1)×(р+1) – матрица в случае комплексных синусоид в белом шуме имеет следующую структуру:
,
где I — единичная (р+1) × (р+1) — матрица, а 
— вектор сигнала размерности р+1, несущий информацию о частоте i-й синусоиды. Матрицу Rp можно представить как сумму автокорреляционной матрицы сигнала Sp и автокорреляционной матрицы шума Wp:
,
где 
, а 
Матрица сигнала будет иметь следующее разложение по собственным значениям:
,
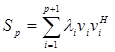Где 
— собственные числа, 
— собственные векторы, причем 
≥ 
> … > 
[4].
Разложение автокорреляционной матрицы на собственные значения можно использовать для получения спектральных оценок или, точнее говоря, улучшенных процедур оценок частоты. Сохранение одной лишь информации, соответствующей собственным векторам подпространства сигнала, эффективно способствует увеличению отношения сигнал/шум, поскольку устраняет вклад мощности компонент подпространства шума.
Для гармонической составляющей в белом шуме наблюдаемым является процесс
,
матричная запись которого имеет следующий вид
(1)
Это выражение представляет собой собственное уравнение процесса, в котором дисперсия шума 
является собственным значением автокорреляционной матрицы Ryy, вектор АРСС – параметров А является собственным вектором, связанным с собственным значением 
, позволяет определить значения АРСС – параметров в том случае, когда известно значение автокорреляционной функции. Это уравнение составляет основу процедуры разложения на собственные числа и позволяет определить точные частоты и мощности р вещественных синусоид в присутствии белого шума, если точно известны 2р+1 значений автокорреляционной функции [4]. Так как известными полагаются только значения автокорреляционной функции, информация о фазе каждой синусоиды теряется.
После нахождения собственных векторов и соответствующих им собственных значений определяются коэффициенты полинома
корни zi=exp(j2πfiΔt), формируемые из этих коэффициентов, будут определять частоты синусоид
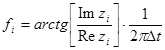
После определения частот по корням полинома для А можно определить мощности синусоид. Значения автокорреляционной функции от Ryy(1) до Ryy(р) можно записать в матричной форме
FP = r , (2)
F =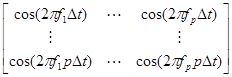 
, P = 
, и r = 
Матрица F состоит из членов, зависящих от частот синусоид, которые определяются посредством нахождения корней полинома. Мощности этих синусоид находятся посредством решения системы уравнений (2) относительно вектора мощности Р.
Очевидно, что данный метод наиболее приспособлен к решению задачи оценивания параметров колебаний, так как в нем доходят до физических параметров сигналов, и одновременно устраняется влияние шума за счет разделения информации на подпространство сигнала и шума.
Однако актуальным останется вопрос обеспечения требуемой точности оценивания параметров сигналов, так как реализация метода сама по себе лишь обеспечивает их вычисление. Следовательно, необходима метрологическая поддержка – методика измерения. Будем исходить из того, что можно создать методику, позволяющую указать погрешности, обеспечиваемые данным методом, а также установить значения параметров регистрации, при которых можно гарантировать обеспечение необходимой точности.
Моделирование. Для оценки точности определения параметров гармонического сигнала были смоделированы различные влияющие факторы. Т.к. моделирование всех зависимостей проводилось параллельно, то значение остальных влияющих факторов, кроме исследуемого, устанавливалось либо по результатам других экспериментов, либо такими образом, чтобы исключить влияние этого параметра.
Квантование сигнала приводит к появлению равномерного шума, а так как на входе алгоритма обработки моделируется выходной сигнал двоичного АЦП, то число уровней квантования оказывает заметное влияние на точность определения параметров сигнала. Отсюда возникает задача – определить число разрядов АЦП, при котором достигаются минимальные погрешности и не изменяются в дальнейшем. Зависимость погрешности от числа разрядов приведена на рисунке 1а).
а)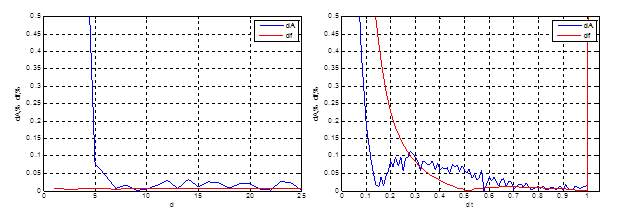
б)
Рисунок 1 – Влияние на погрешность измерения амплитуды и частоты:
а) числа разрядов АЦП; б) шага дискретизации
Откуда видно, что 8-12 разрядов АЦП является вполне достаточным, чтобы минимизировать погрешности при заданном уровне случайных помех. Использование более точного АЦП при приеме исследуемого сигнала является необоснованным в данном случае, т.к. увеличивает стоимость АЦП, но не приводит к повышению точности вычисляемых характеристик сигнала. При этом погрешность остается стабильной на уровне 0,02% и 0,01% для амплитуды и частоты соответственно.
В следующем эксперименте при фиксированном числе отсчетов (N=1000) изменялось значение шага дискретизации в диапазоне 
. При этом максимальный шаг принят за единицу, и шкала 
представлена в долях от максимального шага. Здесь опять видны ограничения частотного диапазона «снизу» и «сверху» (рис 2).
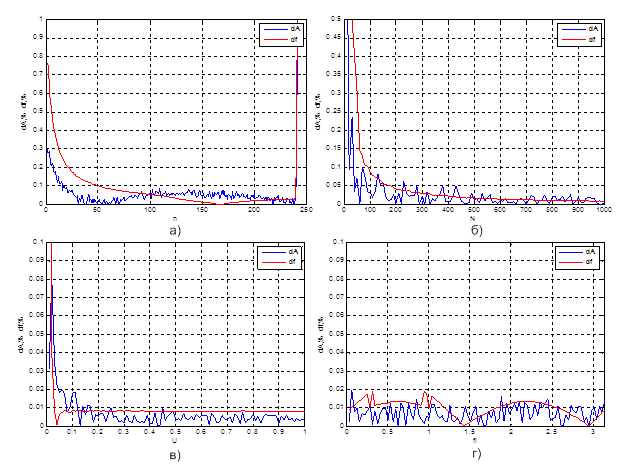
Рисунок 2 – Влияние на погрешность измерения амплитуды и частоты: а) числа периодов, б) числа отсчетов сигнала, в) амплитуды сигнала; г) начальной фазы сигнала.
При исследовании влияния количества периодов за время измерения, показанного на рисунке 2а), было выявлено, что для стабильного определения параметров сигнала необходимо, чтобы количество периодов сигнала было больше пятидесяти, при таком условии погрешности определения параметров находятся на уровне 0,05% и 0,01% для амплитуды и частоты соответственно.
Число точек на период можно исследовать другим способом, зафиксировав число периодов измеряемого сигнала и меняя число отсчетов. Зависимость погрешностей измерения амплитуды и частоты синусоидального сигнала от количества отсчетов приведена на рисунке 2б). По характеру изменения графика можно сделать вывод, что при большом числе отсчетов погрешности начинают уменьшаться. Если принять верхнюю границу равной 1000 отсчетов, то получаем 50 точек на период, а количество отсчетов, которое необходимо для обеспечения стабильно низкой погрешности, составляет 60-80. Это соответствует 3-4 точкам на период.
Значения погрешности от изменения амплитуды сигнала при обработке гармонического колебания в присутствии равномерного шума имеет вид, приведенный на рисунке 2в), при этом погрешность определения амплитуды и частоты в основном составляет 0,05% и 0,01% соответственно, за исключением очень низких уровней сигнала.
На практике процесс измерения не синхронизирован с принимаемым сигналом, поэтому при моделировании гармоническое колебание будет с ненулевой начальной фазой. Отсюда возникает необходимость исследовать влияние начальной фазы на точность контрольных параметров сигнала. Из рисунка 2г) видно, что момент измерения мало влияет на точность обработки полученного с АЦП временного дискретного ряда. Неравномерность кривой обусловлена, скорее всего, влиянием шума.
Также одной из задач является исследование помехоустойчивости обработки данных по методу разложения на собственные числа. При исследовании помехоустойчивости будем рассматривать величину, которая называется коэффициент подавления шума. Он представляет собой отношение сигнал/шум на выходе алгоритма обработки представленных данных к тому же отношению на входе. Будем исследовать зависимость коэффициента подавления от отношения сигнал/шум. Также немаловажным параметром, от которого зависит коэффициент подавления шума, является число двоичных разрядов АЦП.
Из графиков, приведенных на рисунке 5, можно сделать вывод, что использовать этот метод цифрового оценивания имеет смысл уже при отношении сигнал/шум выше 30.
а)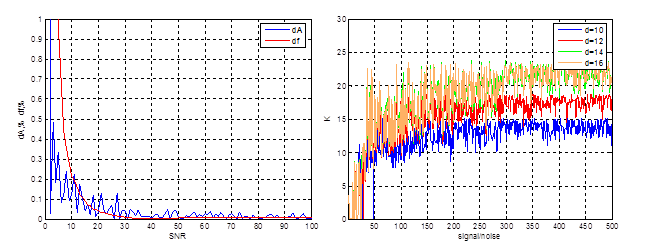
б)
Рисунок 5 – а) график зависимости от отношения сигнал/шум; б) зависимость коэффициента подавления шума
При достаточном количестве разрядов АЦП обработка по методу разложения на собственные числа может успешно использоваться для подавления сильных помех, а при работе со слабозашумленным сигналом, т.е. при больших значениях сигнал/шум, малого количества разрядов АЦП оказывается недостаточным, чтобы обеспечить стабильный коэффициент подавления шума. 12 разрядов АЦП является достаточным, чтобы коэффициент подавления оставался стабильным и при высоких значениях сигнал/шум.
Заключение. В результате проведенной работы были выявлены факторы, обуславливающие погрешность определения параметров гармонического сигнала методом разложения автокорреляционной матрицы сигнала на собственные числа. К этим факторам относятся параметры регистрации (длина реализации, число периодов), оцифровки (разрядность АЦП, шаг дискретизации), условия воспроизведения сигнала (амплитуда и фаза сигнала, уровень шума).
При правильной организации процесса измерения влияние систематической помехи и случайного шума сводится к минимуму, коэффициент подавления шума устанавливается на уровне 15, что свидетельствует о хорошей помехоустойчивости метода даже при низких значениях отношения сигнал/шум.
Полученные результаты исследований подтверждают актуальность использования метода разложения автокорреляционной матрицы сигнала на собственные числа в виртуальных измерительных приборах, и открывают перспективу применения данного метода в микропроцессорах цифровой обработки сигналов.
Рецензенты:
Трофимов А.А., д.т.н., доцент, заместитель начальника учебно-научного центра, ОАО «НИИФИ», г. Пенза.
Бодин О.Н., д.т.н., профессор, ФГБОУ ВПО «Пензенский Государственный Университет», г.Пенза.