Введение
Задача локализации источников роста плотности потока нейтронов (ППН) в реакторе по сигналу ИК, распределённых под активной зоной, актуальна для повышения безопасности установки. Для обеспечения безопасной эксплуатации реактора важно иметь возможность оперативно определять координаты тепловыделяющей сборки (ТВС) или поглощающего стержня, являющихся причиной роста ППН. Локальный рост ППН может возникать, например, вследствие ошибки в ходе перегрузки топливных сборок или при самопроизвольном перемещении стержней системы управления и защиты (СУЗ). Независимо от причины возникновения локального роста ППН в задачу системы контроля энерговыделения (СКЭ) входит определение его координат и выдача рекомендаций по блокировке извлечения ближайших стержней СУЗ.
Известны решения подобных задач (определение координат источника излучения по сигналу трёх детекторов) для случая электромагнитного излучения. Для этого случая задача упрощается, так как известны скорость распространения электромагнитных волн и зависимость интенсивности излучения от расстояния между источником и приёмником. Два распространённых метода локализации источника электромагнитного излучения – трилатерация [3] и мультилатерация [4]. В работе [5] описан метод локализации источника нейтронного излучения в городских условиях с помощью сети детекторов нейтронов, распределённых по городу. Для локализации необходимо три или более детектора, регистрирующие повышенный уровень нейтронного излучения. Локализация источника повышенной ППН в активной зоне реакторов типа ВВЭР описана в работе [1]. Контроль неравномерностей поля энерговыделения в реакторах данного типа, как правило, осуществляется с помощью большого числа датчиков нейтронов, распределённых внутри активной зоны.
Методы трилатерации [3] и мультилатерации [4] нельзя применить для задачи определения двухмерных координат источника роста ППН в активной зоне реактора, так как зависимость сигнала детектора от расстояния до источника имеет более сложный вид, чем квадратичная зависимость в случае точечного источника электромагнитного излучения. Метод локализации источника нейтронов в городских условиях [5] не применим к задаче локализации всплеска энерговыделения по активной зоне реактора, так как в нём заложена квадратичная зависимость сигнала датчиков нейтронов от расстояния. Такое упрощение не применимо к сигналу ИК рассматриваемого реактора, регистрирующих нейтронное излучение активной зоны больших размеров. Использование множества внутризонных датчиков для контроля поля энерговыделения в активной зоне, как на реакторах типа ВВЭР [1], на рассматриваемом реакторе также неосуществимо. Расположить датчики нейтронного потока внутри активной зоны данного реактора невозможно по конструктивным причинам. Также по конструктивным и экономическим соображениям невозможно значительно увеличить количество подзонных ИК.
Задачи данной работы:
1) предложить алгоритм определения двухмерных координат источника локального роста ППН в активной зоне ядерного реактора, использующий в качестве входных данных координаты трёх подзонных камер и их токовые сигналы;
2) реализовать предлагаемый алгоритм в виде программы для персонального компьютера и протестировать его с использованием данных, полученных в ходе испытаний на рассматриваемом реакторе в 2007-2008 годах, в которых регистрировались сигналы подзонных камер при внесении в отдельные ячейки дополнительной реактивности.
Подзонные ИК входят в систему СКЭ, контролирующую энерговыделение в активной зоне. В задачу системы СКЭ входит определение координат источника локального роста ППН на энергетических уровнях мощности реактора, выдача этой информации оператору и рекомендации по блокировке стрежней СУЗ, перемещаемых вблизи источника роста ППН.
Метод решения задачи и описание эксперимента в обоснование алгоритма
При решении задачи была использована двухмерная модель. Сигнал подзонной ИК, регистрирующей рост ППН, также зависит от неравномерной загрузки активной зоны и выгорания топлива в ближайших ТВС. Непосредственный нейтронно-физический расчёт сигналов подзонных ИК при возникновении в активной зоне локального роста ППН пока не представляется возможным из-за сложностей, связанных с заданием начальных условий, описывающих текущий вариант загрузки и выгорание
На рисунке 1 показан фрагмент активной зоны в проекции на горизонтальную плоскость. Показано возможное расположение ячейки-источника роста реактивности и камер, регистрирующих рост ППН. Серым цветом закрашены ячейки, в которых находятся поглощающие стержни СУЗ. Расстояние между центрами соседних стержней СУЗ – 2,65 шага решётки.
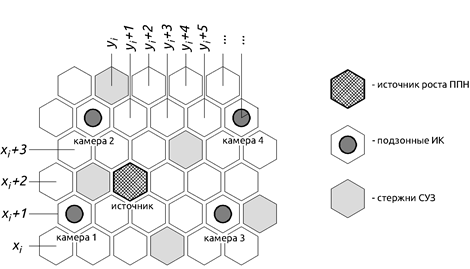
Рисунок 1. Фрагмент активной зоны с возможным расположением источника роста ППН и трёх камер, регистрирующих этот рост
В данном алгоритме в качестве меры скорости изменения ППН, регистрируемой камерами, выбрано изменение токового сигнала i камеры за некоторое время t (1).
![]() ,(1)
,(1)
Алгоритм определяет координаты источника роста ППН неизвестной величины, используя экспериментально полученную зависимость изменения сигнала подзонной камеры от расстояния до источника роста ППН. Зависимость была получена в ходе проведения испытаний прототипа системы СКЭ на реакторе до его остановки, в ходе которых осуществлялось внесение в отдельные ячейки активной зоны дополнительной реактивности.
С учётом усреднения сигналов ИК при различных вариантах загрузки активной зоны и различном выгорании в рассмотренных испытаниях, зависимость сигнала ИК от расстояния до источника роста ППН была приближена радиально симметричной функцией Ψ(r), гладкой и непрерывной на промежутке от нуля до бесконечности. Физический смысл функции Ψ(r) – величина сигнала камеры, находящейся на расстоянии r от источника всплеска реактивности, по отношению к сигналу камеры, если бы она находилась непосредственно под источником (r=0). Функция Ψ(r) имеет вид, показанный на рисунке 2.
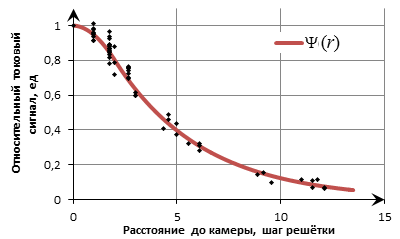
Рисунок 2. Функция относительного сигнала камер от расстояния до источника роста ППН
Степень соответствия экспериментальным точкам выбранной кривой была оценена с помощью коэффициента детерминации R2 [2], вычисляемого по формуле (2):
![]() (2)
(2)
где ![]() – сумма квадратов остатков регрессии,
– сумма квадратов остатков регрессии, ![]() ,
, ![]() – фактические и расчётные значения переменной, а
– фактические и расчётные значения переменной, а ![]() – сумма квадратов отклонений от среднего. Коэффициент детерминации приближения выбранной кривой: R2=0,981.
– сумма квадратов отклонений от среднего. Коэффициент детерминации приближения выбранной кривой: R2=0,981.
Используется предположение, что относительное изменение сигналов камер, находящихся на различном расстоянии от источника роста ППН, растёт пропорционально друг другу. Пусть в некоторой ячейке имеется источник роста реактивности и камера, находящаяся непосредственно под этой ячейкой, регистрирует изменение ППН на W процентов, тогда относительное изменение сигнала Ii камеры, находящейся на расстоянии ri , будет равно:
![]() ,(3)
,(3)
Была проведена оценка соответствия выбранной радиально симметричной функции существующим теоретическим расчётам, описывающим вклад каждой из ТВС в сигнал подзонной ИК. Для этого было проведено сравнение сигнала ИК, вычисленного по формуле (3) с сигналом, теоретически вычисленным как сумма вкладов каждой из ТВС, находящейся в радиусе 5 шагов решётки от ИК. Расхождения теоретического сигнала ИК и сигнала, вычисленного с помощью эмпирической функции Ψ(r), составило от 0 до 13% в зависимости от взаимного расположения источника роста ППН и ИК, что подтверждает достаточное соответствие существующих теоретических расчётов и выбранной упрощающей модели.
Также в алгоритме используется обратная функция Ψ -1(I) , определяющая расстояние от ИК до источника всплеска реактивности, вызывающего относительное изменение сигнала на 100% в ИК, находящейся непосредственно под этим источником. При этом, Ψ(Ψ -1(r))= r. Функция Ψ ?1(I) показана на рисунке 3.
![]()
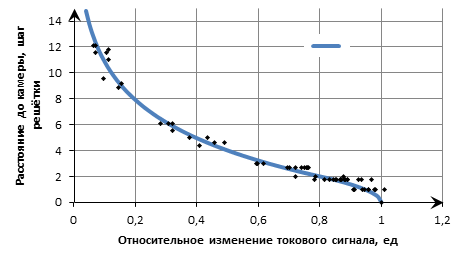
Рисунок 3. Функция расстояния до источника роста ППН от сигнала камеры
Алгоритм работает следующим образом.
При регистрации одной из подзонных ИК изменения сигнала, превышающего выбранную уставку, из всех подзонных ИК выбираются три, регистрирующие наибольшее изменение сигнала. Координаты этих камер и регистрируемые ими сигналы используются в качестве входных данных алгоритма.
Используя функцию Ψ(r), можно выразить относительные изменения сигналов трёх камер через неизвестные расстояния до источника всплеска реактивности:
![]() , (4)
, (4)
где I1,2,3 – относительное изменение сигнала трёх ИК, r1,2,3 – расстояние от ИК до источника всплеска ППН, W – теоретическое относительное изменение сигнала камеры, находящейся непосредственно под ячейкой – источником всплеска ППН. Таким образом, зная сигналы ИК, можно выразить через расстояние от одной из камер – r1 – расстояния от двух других камер до источника – r2 и r3:
![]() (5)
(5)
Суть алгоритма поиска источника заключается в поиске точки, расстояния от которой до камер удовлетворяют выражениям (5). Геометрический смысл задачи – поиск точки пересечения трёх окружностей с известными координатами центров и радиусами, связанными выражением (5).
Алгоритм заключается в поиске значения r1, при котором три окружности с радиусами, связанными выражением (5), пересекутся в одной точке. Задавшись некоторым значением r1, и получив из (5) значение r2, можно геометрически рассчитать расстояние от точек пересечения окружностей c радиусом r1 с центром в точке (x1, y1) и радиусом r2 с центром в точке (x2, y2) до третьей ИК в точке (x3, y3). Геометрическая задача показана на рисунке 4.
Рисунок 4. Геометрическая задача поиска расстояния от точек пересечения двух окружностей до центра третьей окружности.
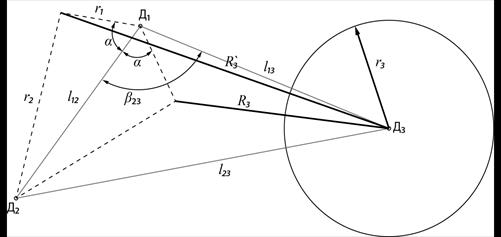
l12, l23, l13 – отрезки, соединяющие центры трёх ячеек, под которыми находятся ИК, длины отрезков равны расстояниям между соответствующими камерами,
R3 и R3' – соответственно меньшее и большее расстояния от третьей ИК до точки пересечения первой и второй окружностей,
a – угол между отрезком, соединяющим центр первой окружности и точками пересечения первой и второй окружности, и отрезком l12. Угол a может принимать значения от 0° до 180°,
β23 – меньший (от 0° до 180°) угол между отрезками l12 и l13,
β23ПОЛН – полный (от 0° до 360°) угол между отрезками l12 и l13.
Задача сводится к нахождению такого r1, при котором расстояния R3, R3' будут равны ![]() , таким образом, все три радиуса будут удовлетворять выражению (5).
, таким образом, все три радиуса будут удовлетворять выражению (5).
Угол a можно выразить через радиус первой окружности, записав теорему косинусов для треугольника со сторонами![]()
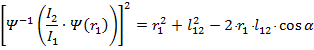 (6)
(6)
Большее и меньшее расстояния от третьей камеры (центра третьей окружности) до точек пересечения первой и второй окружности можно записать, используя теорему косинусов (рисунок 4):
![]() (7)
(7)
![]() (8)
(8)
Так как β23 и a изменяются в пределах от 0 до 180, то R3 ≤ R3' . При этом R3 будет равно R3' только в граничном случае, когда все три камеры находятся на одной прямой.
Введём функции fr(r1) и fR(r1):
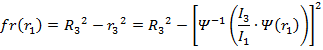 (9)
(9)
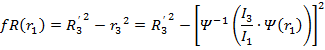 (10)
(10)
Корни уравнений fr(r1)=0 и fR(r1)=0 – это значения радиуса первой окружности, при котором все три окружности пересекаются в одной точке. Подставив ![]() и
и ![]() из (7)-(8) в (9)?(10), получим:
из (7)-(8) в (9)?(10), получим:
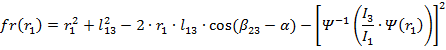 (11)
(11)
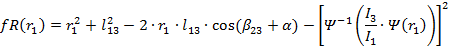 (12)
(12)
Функции (11)-(12) будут определены при существовании точек пересечения окружностей, соответствующих первой и второй камерам. Обозначим граничные значения отрезка, на котором определены (11)-(12), как rmin и rmax. Минимальное значение, при котором определены функции (11)-(12), определяется как радиус, при котором происходит первое касание окружностей, соответствующих первой и второй камерам, и находится из выражения (13):
![]() (13)
(13)
Максимальное значение, при котором определены функции (11) и (12), соответствует моменту, когда одна из двух окружностей окажется внутри другой, и определяется из выражения (14):
![]() (14)
(14)
Соответственно, в граничных точках – rmin и rmax – значения функций fr(r1) и fR(r1) будут равны, так как при этих значениях окружности, соответствующие первой и второй камерам, касаются в одной точке. Во всех других точках отрезка [rmin, rmax] функции различны, вне отрезка [rmin, rmax] функции (11)-(12) – не определены.
В используемой программе корни уравнений были рассчитаны методом бисекции.
В результате решения совокупности уравнений (11)-(12) получается значение расстояния от первой ИК до источника. Зная это расстояние, можно восстановить координаты предполагаемого источника.
Тестирование метода на модельной задаче
Алгоритм был реализован в программе для ПК на языке С++ и был опробован на результатах испытаний, проведённых на реакторе в 2007-2008 годах, в которых создавались источники локального роста ППН в отдельных ячейках.
В качестве входных данных для программы задавались координаты трёх ИК и величина изменения их токового сигнала, соответствующие различным состояниям реактора в ходе испытаний. Затем предполагаемые координаты источника, рассчитанные программой по предложенному алгоритму, сравнивались с координатами источника всплеска реактивности, в действительности использованного в данный момент испытаний. Сравнение предсказаний алгоритма и фактических координат источника роста реактивности показано в таблице 1.
Таблица 1. Сравнение предсказаний алгоритма с действительными координатами источника
|
Действительный номер ячейки |
Предсказанный номер ячейки |
Δx, шаг решётки |
Δy, шаг решётки |
Расстояние от реальной ячейки, шаг решётки |
||
|
20 |
29 |
19,29 |
28,80 |
0,71 |
0,19 |
0,62 |
|
20 |
29 |
18,97 |
29,46 |
1,02 |
-0,47 |
0,92 |
|
20 |
29 |
18,97 |
29,46 |
0,16 |
0,30 |
0,20 |
|
20 |
29 |
19,83 |
28,65 |
0,17 |
0,34 |
0,23 |
|
20 |
29 |
19,92 |
28,36 |
0,08 |
0,63 |
0,32 |
|
20 |
29 |
19,92 |
28,36 |
0,47 |
0,29 |
0,43 |
|
21 |
16 |
21,34 |
14,65 |
-0,34 |
1,35 |
0,74 |
|
21 |
16 |
21,45 |
15,01 |
-0,45 |
0,98 |
0,63 |
|
21 |
16 |
21,41 |
15,37 |
-0,41 |
0,63 |
0,48 |
|
21 |
30 |
20,51 |
29,39 |
0,48 |
0,61 |
0,52 |
|
21 |
30 |
20,01 |
29,59 |
0,98 |
0,40 |
0,88 |
|
21 |
30 |
20,40 |
29,15 |
0,59 |
0,84 |
0,67 |
|
21 |
30 |
20,65 |
29,11 |
0,35 |
0,89 |
0,53 |
|
21 |
30 |
20,40 |
29,19 |
0,59 |
0,80 |
0,65 |
|
21 |
30 |
20,59 |
28,98 |
0,40 |
1,01 |
0,62 |
|
21 |
30 |
20,87 |
29,21 |
0,12 |
0,78 |
0,40 |
|
21 |
30 |
19,96 |
29,58 |
1,03 |
0,42 |
0,92 |
|
21 |
30 |
20,70 |
28,77 |
0,30 |
1,23 |
0,67 |
|
21 |
30 |
20,93 |
29,12 |
0,07 |
0,87 |
0,44 |
|
21 |
30 |
20,08 |
29,44 |
0,91 |
0,56 |
0,84 |
|
21 |
30 |
20,77 |
28,69 |
0,23 |
1,30 |
0,68 |
|
21 |
30 |
20,95 |
29,13 |
0,05 |
0,86 |
0,43 |
|
21 |
30 |
20,11 |
29,45 |
0,89 |
0,55 |
0,82 |
|
21 |
30 |
20,79 |
28,70 |
0,21 |
1,29 |
0,67 |
|
21 |
30 |
21,09 |
29,37 |
-0,09 |
0,62 |
0,32 |
|
21 |
30 |
19,86 |
29,98 |
1,13 |
0,01 |
0,98 |
|
21 |
30 |
20,89 |
28,79 |
0,11 |
1,20 |
0,61 |
|
Средняя ошибка, шаг решётки |
0,60 |
|||||
|
Максимальная ошибка, шаг решётки |
0,98 |
|||||
|
Минимальная ошибка, шаг решётки |
0,20 |
|||||
Кроме того, в качестве входных данных были заданы сигналы камер, искажённые погрешностью измерительных каналов (примерно 0,2%) и флуктуациями ППН на рассматриваемых уровнях мощности (до 1%). Ошибки в предсказаниях, вызванные этими факторами, не превысили минимальную ошибку в 0,28 шага решётки, полученную при обработке алгоритмов исходных экспериментальных данных.
Обсуждение результатов
Алгоритм исправно определял местоположение источника всплеска ППН с ошибкой не более одного шага решётки независимо от величины внесённой реактивности. Более того, из рассчитанных координат источника и сигнала трёх камер можно вычислить условную «амплитуду» всплеска – W – сигнал гипотетической подзонной ИК, находящейся непосредственно под ячейкой, в которую была внесена дополнительная реактивность.
Наличие ошибок можно объяснить тем, что реальная зависимость сигнала камеры от расстояния не является радиально симметричной и зависит от многих факторов, таких как расположение поблизости погружённых стержней СУЗ, неравномерная загрузка активной зоны и выгорание, влияние которых в данной работе не учитывалось при использовании функции Ψ(r).
При поведении эксперимента в некоторых случаях в результате решения уравнений (12)-(13) получалось два корня и, соответственно, две возможные пары координат предполагаемого источника. В таком случае неверный источник можно отбросить, исходя из дополнительных условий. Например, найденную точку можно считать ложной, если её координаты выходят за область активной зоны или если она находится ближе в камере, зарегистрировавшей меньшее изменение сигнала, чем три камеры, используемые в алгоритме.
Необходимо совершенствование алгоритма с учётом расширения доступных данных. В дальнейшем, при проведении испытаний уже на модернизированном реакторе, следует получить данные для уточнения вида зависимости Ψ(r). Также, используя эти данные, можно будет скорректировать функцию Ψ(r) с учётом возможных конструктивных изменений в активной зоне, сделанных в ходе модернизации реактора.
Заключение
На основе данных, полученных в ходе испытаний по регистрации сигналов подзонных камер при внесении в активную зону возмущений по реактивности, проведённых в 2007-2008 годах на реакторе, был разработан алгоритм определения координат источника аномального роста ППН.
Алгоритм базируется на использовании координат и сигналов трёх подзонных ионизационных камер деления, регистрирующих наибольшее относительно изменение ППН. Разработанный алгоритм был реализован в программе для персонального компьютера на языке C++. В ходе тестирования алгоритма в качестве входных данных задавались координаты и сигналы камер, регистрировавших локальный рост ППН в ходе испытаний, проведённых на реакторе в 2007-2008 годах.
Результаты сравнения предсказаний алгоритма и действительных координат источника повышения ППН находятся в хорошем соответствии. Ошибка определения координат не превышает одного шага решётки активной зоны. Средняя ошибка в определении координат – 0,60 шага решётки. Погрешность, обусловленная флуктуацией сигналов ИК и оцифровкой токового сигнала измерительной аппаратурой, примерно на порядок меньше погрешности, обусловленной отклонением реальных сигналов ИК от приближённой функции Ψ(r) .
В будущем для совершенствования работы алгоритма необходимо проведение испытаний для уточнения формы зависимости Ψ(r). Для повышения точности полученных результатов следует учесть влияние на сигналы камер положения ближайших стержней СУЗ.
Данный алгоритм может быть использован для поиска в двухмерных координатах источника возмущений, для которых теоретически или экспериментально получена некоторая зависимость величины сигнала от расстояния – Ψ(r). Для использования данного алгоритма не требуется знать интенсивность источника возмущения.
Автор выражает благодарность Б.В. Кутееву за помощь в обсуждении результатов.
Рецензенты:
Пупков К.А., д.т.н., профессор, заведующий кафедрой кибернетики и мехатроники, Российский университет дружбы народов, г. Москва.
Кутеев Б.В., д.ф.-м.н., профессор, начальник отдела термоядерных реакторов, ИФТ КЦЯТ НИЦ «Курчатовский институт», г. Москва.



