Введение
Увеличение мощности в единице оборудования может быть достигнуто за счет параллельной работы нескольких силовых модулей. В частности, этот прием часто применяется в системах электроснабжения на основе устройств силовой электроники. В настоящей работе решается задача построения линеаризованной модели системы распределения мощности между компенсированными инверторами тока, объединенными по выходу. Такая модель необходима при исследовании динамических процессов в системе при изменении нагрузки или напряжения питающей сети.
Цель исследования
Разработка методики моделирования динамических режимов систем распределения мощности между объединёнными по выходу силовыми преобразователями.
Выбор и обоснование метода
Известно, что практическое использование параллельного инвертора тока без использования компенсаторов избыточной реактивной мощности конденсаторной батареи ограничено. Мягкая внешняя характеристика не позволяет использовать его для питания сильно меняющейся нагрузки. Для стабилизации внешней характеристики параллельного инвертора применяют его совместную работу с тиристорно-реакторными или диодно-реакторными компенсаторами [2].
На рис. 1 и 2 показаны схемы однофазных инверторов тока с тиристорно-реакторными (ТРК) и диодно-реакторными компенсаторами (ДРК).
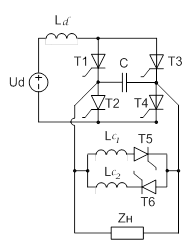
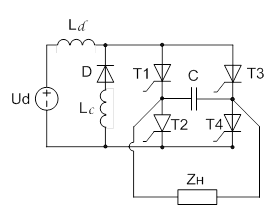
Рисунок 1. Однофазный инвертор тока с тиристорно-реакторным (слева) и с диодно-реакторным (справа) компенсаторами
Отличие работы ТРК и ДРК состоит в характере управления током в реакторе компенсатора. В ТРК длительность токопротекания через реактор задается внешней системой автоматического управления, тогда как в ДРК длительность компенсирующего импульса тока реактора определяется углом запирания β [2].
Строго говоря, оба инвертора являются нелинейными объектами, т.е. непосредственное применение методики построения линейной дискретной динамической модели к ним неправомерно. Однако для каждой из них можно предложить прием аппроксимации процесса компенсации, который приводит к линейной модели. Покажем это для инвертора тока с ТРК.
На интервале симметрии инвертор с ТРК последовательно принимает три состояния, показанные на рис. 2. Соответствующие эпюры токов реакторов компенсатора и напряжения на коммутирующем конденсаторе приведены на рис. 3.
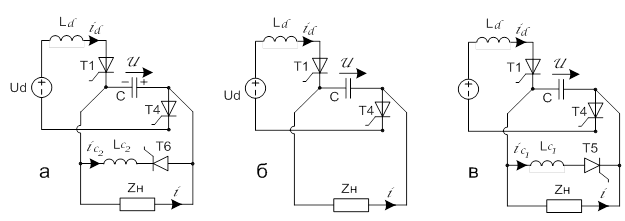
Рисунок 2. Состояния инвертора с ТРК на интервале симметрии
На первом подынтервале [0, θ1] (рис. 3 слева) реализуется состояние инвертора, показанное на рис. 2а. В начале этого подынтервала включились тиристоры Т1 и Т4, что благодаря показанной на рисунке полярности напряжения u привело к выключению ранее проводивших ток тиристоров Т2 и Т4. Тиристор Т6, включенный на предыдущем интервале, проводит токic2 индуктивности![]() , который имеет отрицательное значение.
, который имеет отрицательное значение.
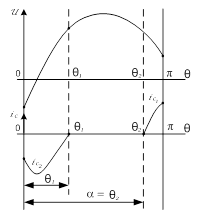
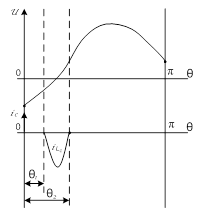
Рисунок 3. Эпюры выходного напряжения и тока реактора Lc инвертора с ТРК на интервале симметрии при α < π (слева) иα > π (справа)
Поскольку напряжение u, перезаряжаясь током id, меняет знак, то ток ![]() , увеличивающийся по абсолютной величине, пока сохраняется отрицательное значение напряжения, начинает уменьшаться по модулю и в момент времени, соответствующий электрическому углу q1, становится равным нулю.
, увеличивающийся по абсолютной величине, пока сохраняется отрицательное значение напряжения, начинает уменьшаться по модулю и в момент времени, соответствующий электрическому углу q1, становится равным нулю.
С этого момента наступает второе состояние (второй подынтервал, рис. 2 б). Оно заканчивается, когда на тиристор Т5 подается управляющий импульс и, поскольку напряжение u в этот момент θ2 положительное, он открывается. Под действием напряжения u в индуктивности ![]() развивается импульс тока
развивается импульс тока ![]() (рис. 3, подынтервал [θ2, π]).
(рис. 3, подынтервал [θ2, π]).
Если импульсы токов индуктивности ![]() и
и ![]() не перекрываются во времени, то вместо двух индуктивностей используют однуиндуктивность Lc. При этом ток этой индуктивности состоит из двух разнополярных колоколообразных импульсов, длительность каждого из которых регулируется моментом подачи импульса на соответствующий тиристор ТРК (на рассматриваемом интервале это Т5, момент времени θ2).
не перекрываются во времени, то вместо двух индуктивностей используют однуиндуктивность Lc. При этом ток этой индуктивности состоит из двух разнополярных колоколообразных импульсов, длительность каждого из которых регулируется моментом подачи импульса на соответствующий тиристор ТРК (на рассматриваемом интервале это Т5, момент времени θ2).
Для регулирования напряжения на выходе инвертора необходимо изменить коэффициент передачи по напряжению. При этом, чем меньше длительность и амплитуда импульсов тока ![]() , тем большее значение имеет этот коэффициент и, наоборот, при их увеличении коэффициент передачи инвертора по напряжению уменьшается. По определению коэффициент передачи инвертора по напряжению равен
, тем большее значение имеет этот коэффициент и, наоборот, при их увеличении коэффициент передачи инвертора по напряжению уменьшается. По определению коэффициент передачи инвертора по напряжению равен
![]()
где U – действующее напряжение на выходе инвертора, Ud – постоянное значение напряжения на его выходе.
В предположении о синусоидальности кривой выходного напряжения длительность каждого из разнополярных импульсов тока ![]() равна
равна ![]() где
где
![]()
Здесь α – электрический угол управления, равный углу задержки относительно начала соответствующего интервала импульса, открывающего очередной тиристор ТРК (в нашем случае ![]() , рис. 3); b – угол запирания рабочего тиристора, соответствующий моменту смены знака выходного напряжения на интервале.
, рис. 3); b – угол запирания рабочего тиристора, соответствующий моменту смены знака выходного напряжения на интервале.
Если угол ![]() задается системой управления ТРК и может считаться известным, то угол b является функцией параметров схемы инвертора и нагрузки.
задается системой управления ТРК и может считаться известным, то угол b является функцией параметров схемы инвертора и нагрузки.
В [4] показано, что при регулировании по цепи питания инвертора и постоянной нагрузке угол b изменится незначительно (2–3 %). Это значение угла может быть найдено из следующего нелинейного уравнения
![]()
где 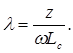
Определив из этого уравнения угол b при данных значениях параметров нагрузки Z,![]() , параметров схемы C и Lc, частоты w и угла α, мы можем найти значения угла d, а, следовательно, длительность каждого из подынтервалов а, б, в (рис. 2).
, параметров схемы C и Lc, частоты w и угла α, мы можем найти значения угла d, а, следовательно, длительность каждого из подынтервалов а, б, в (рис. 2).
Из второго из этих рисунков имеем длительность первого подынтервала
![]()
длительность второго подынтервала
![]()
длительность третьего подынтервала
![]()
При α > π последовательность состояний меняется. В начале интервала имеет место состояние б рис. 2, поскольку импульс управления, последовательный на тиристоре Т6 при α > π, задерживается с предыдущего интервала. Если α < π+β, то при θ = α-π возникает состояние а рис. 2.
Если α > π+β, то этого не происходит, поскольку напряжение на конденсаторе в момент подачи импульса на Т6 имеет запирающую полярность. Поэтому в этом случае инвертор функционирует как параллельный инвертор без компенсатора.
Состояние а имеет место, пока ток через реактор ![]() сохраняет направление, проводящее для тиристора Т6. В момент прохождения этого тока через нуль инвертор снова переходит в состояние б и находится в нем до конца интервала.
сохраняет направление, проводящее для тиристора Т6. В момент прохождения этого тока через нуль инвертор снова переходит в состояние б и находится в нем до конца интервала.
Из рис. 2 длительность первого подынтервала в случае α > π+β равна
![]()
длительность второго подынтервала
![]()
длительность третьего подынтервала
![]()
Случай α = π фактически сводит работу инвертора с ТРК к работе инвертора с ДРК, так как ток в индуктивности Lc начинается в начале интервала (см. рис. 2).
Таким образом, при сделанных предположениях, используя знание моментов перехода инвертора из одного состояния в другое, мы можем построить дискретную динамическую модель инвертора с ТРК при его управлении по цепи питания со стороны звена постоянного тока. Именно такой способ управления потоками энергии через инверторы используется в системе распределения мощности между инверторами тока с ТРК, блок-схема которой приведена на рис. 4.
Динамическая модель системы распределения для инверторов с ТРК строится по методике, описанной в работе [5].
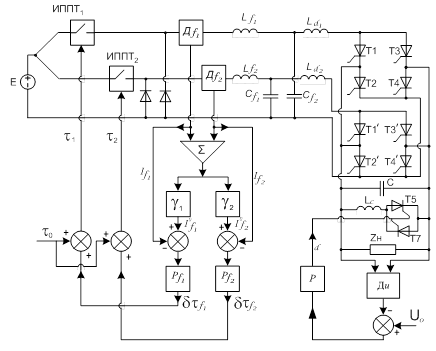
Рисунок 4. Блок-схема системы распределения мощности для двух инверторов с ТРК
Отличие рассматриваемой системы (рис. 4) от системы распределения мощности между некомпенсированными инверторами [3] состоит в отсутствии «смешивания» сигналов обратной связи системы стабилизации выходного напряжения и системы распределения мощности. В результате обе автоматические системы функционируют автономно, что обеспечивает развязку переходных процессов в этих системах. Сказанное позволяет строить динамическую модель системы распределения независимо от системы стабилизации, ограничившись параметрическим влиянием угла ![]() управления цепью ТРК через силовое воздействие импульсов тока индуктивности Lc на исследуемые процессы.
управления цепью ТРК через силовое воздействие импульсов тока индуктивности Lc на исследуемые процессы.
Сначала рассмотрим случайα < π. Поскольку на интервале симметрии инвертора в данном случае последовательно возникают три состояния силовой схемы, то мы получаем три соответствующие системы дифференциальных уравнений (ДУ).
![]()
![]()
![]()
Вектор переменных состояния имеет вид
![]()
Матрица L имеет вид
![]()
Сами системы ДУ отличаются только матрицами при векторе состояния ![]() , которые имеют следующий вид:
, которые имеют следующий вид:
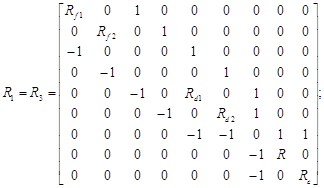
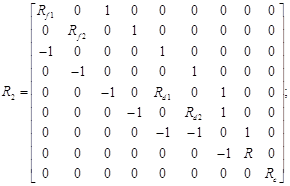
Очевидно, что эти отличия определяются наличием или отсутствием на соответствующем подынтервале тока индуктивности Lc.
Длительности временных подынтервалов, в течение которых справедливы системы уравнений, определены выше. Поэтому эти значения τ1, τ2, τ3 мы считаем заданными.
После записи системы ДУ в форме Коши
![]()
где ![]()
находим значения расчетного вектора ![]() в граничные моменты указанных подынтервалов:
в граничные моменты указанных подынтервалов:
![]()
![]()
![]()
Здесь мы, как и ранее, используем матричные экспоненты![]() ,
,![]() ,
,![]() , позволяющие компактно записать результат решения ДУ аналитическим методом [1]. Вектор
, позволяющие компактно записать результат решения ДУ аналитическим методом [1]. Вектор ![]() представляет собой вектор входных напряжений разомкнутой системы.
представляет собой вектор входных напряжений разомкнутой системы.
Объединяя записанные решения для подынтервалов и используя метод одного интервала, для значения вектора расчетных переменных в начале следующего интервала получаем равенство
![]()
где в данном случае
![]()
получаем искомую связь между двумя последовательными значениями и, т.е. дискретную динамическую модель разомкнутой системы
![]()
где
![]()
![]()
Для получения модели замкнутой системы распределения дополним последние соотношения уравнениями обратных связей и регуляторов
![]()
![]()
В матрично-векторной форме уравнение для вектора ![]() теперь может быть записано так:
теперь может быть записано так:
![]()
где
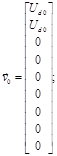
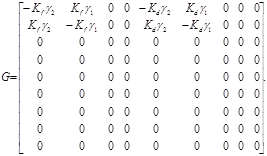
Здесь ![]() – текущее значение выпрямленного напряжения, подаваемого на вход ИППТ.
– текущее значение выпрямленного напряжения, подаваемого на вход ИППТ.
Подставив последнее выражение для вектора![]() в уравнение разомкнутой системы, получим окончательную дискретную динамическую модель замкнутой системы распределения мощности
в уравнение разомкнутой системы, получим окончательную дискретную динамическую модель замкнутой системы распределения мощности
![]()
где
![]()
В случаеα > π порядок сомножителей в формулах для матриц D и F модели системы меняется. Эти матрицы в этом случае имеют вид
![]()
![]()
Построенная модель системы распределения была использована при исследовании ее динамики и выборе коэффициентов усиления регуляторов.
Заключение
Разработанная модель служит основой для исследования систем заданного автоматического распределения нагрузки между объединенными по выходу силовыми агрегатами. Информация о динамических свойствах системы и о влиянии отдельных параметров на устойчивость и качество регулирования содержится в матрице D модели и прежде всего в ее спектре.
Рецензенты:
Игнатьев А.А., д.ф.-м.н., профессор, заведующий кафедрой «Автоматизация, управление, мехатроника» Саратовского государственного технического университета имени Гагарина Ю. А., г. Саратов.
Коломейцев В.А., д.т.н., профессор кафедры «Радиоэлектроника и телекоммуникации» Саратовского государственного технического университета имени Гагарина Ю. А., г.Саратов.



