В современном мире активизируется академическая мобильность, расширяются международные контакты, происходит глобализация и интернационализация образования. Рост числа иностранных студентов делает актуальной проблему обучения на неродном языке в неродной социокультурной среде. В связи с расширением масштабов высшего образования остро встает проблема качества обучения. Факторами повышения качества и эффективности высшего образования являются академическая мобильность и предоставление образовательных услуг [3].
Одной из задач Программы повышения конкурентоспособности Национального исследовательского Томского политехнического университета среди ведущих мировых научно-образовательных центров в области совершенствования образовательной деятельности на 2013–2020 гг. является совершенствование организации учебного процесса, что предполагает снижение доли аудиторной работы студентов (лекций), повышение роли ресурсно-обеспеченной самостоятельной работы [4]. Также в Программе делается акцент на интернационализацию образования, что должно повлечь за собой привлечение в университет иностранных студентов.
Современные тенденции модернизации вузовского образования ориентированы на развитие личности студента – на личностно-ориентированный подход. В связи с этим уделяется повышенное внимание созданию образовательных технологий, при которых основная цель преподавателя – это активизация и поддержка профессионального саморазвития студентов, организация самоуправляемой учебной деятельности. Основой образовательного процесса становится самостоятельная работа студентов (СРС), которая носит непрерывный и систематический характер на протяжении всего периода обучения в вузе.
С помощью СРС осуществляется главная функция образования – получение новых знаний, закрепление и превращение их в устойчивые умения и навыки, формирование профессиональных компетенций будущих выпускников. Некоторыми из факторов, от которых зависит эффективность самостоятельной работы, являются характер знаний, источники знаний, организация самостоятельной работы. При обучении иностранных студентов необходимо учитывать неоднородность аудитории по уровню знаний, степени владения и восприятия дисциплины на неродном языке. Задача преподавателей общенаучных и общепрофессиональных дисциплин: формирование уровня предметной грамотности на фоне недостаточного уровня владения русским языком иностранных студентов [2]. Таким образом, коммуникативная и академическая адаптация являются главными условиями для успешного обучения иностранных студентов в техническом вузе.
Необходимость осуществлять учебно-познавательную деятельность студентов на неродном языке сталкивается с комплексом проблем, вследствие чего снижается эффективность учебной деятельности [3]. К таким проблемам относятся:
- недостаточно высокий уровень владения русским языком для усвоения предлагаемого теоретического материала;
- низкий уровень базовой подготовки;
- трудности в освоении специальной терминологии;
- отсутствие опыта творческой и профессиональной деятельности.
В результате иностранным студентам требуется больше времени для усвоения материала, а преподавателям – для объяснения необходимого учебного материала.
В связи с этим для организации самостоятельной работы иностранных студентов, обучающихся на русском языке, и для повышения эффективности академической адаптации иностранных студентов в российском вузе возникла необходимость в разработке и создании учебно-методического комплекса по математике.
Математический текст, предназначенный для иностранных студентов, имеет свои особенности конструирования. Отметим некоторые из них:
- объем текста должен быть относительно небольшим;
- тексты должны иметь достаточно прозрачную структуру;
- языковое оформление текста должно способствовать вычленению ключевой информации по теме.
На основе десятилетнего опыта работы с иностранными студентами преподавателями математики междисциплинарной кафедры ТПУ ведется активная работа по созданию учебных пособий для обеспечения учебного процесса иностранных студентов. Авторы статьи совместно с преподавателем кафедры Русского языка как иностранного Л.И. Ярицей разработали учебное пособие «Математика 1. Линейная алгебра и аналитическая геометрия» объемом 15,18 условных печатных листов. Содержание пособия соответствует его названию и рабочей программе по дисциплине «Математика. Линейная алгебра и аналитическая геометрия» (80 академических часов: 24 ч. лекций, 24 ч. практических занятий, 32 ч. самостоятельной работы).
При составлении пособия авторы ставили цели:
- изложить материал в доступной форме на русском языке;
- помочь иностранным студентам овладеть математической терминологией на русском языке;
- активизировать лексический запас иностранных студентов при ответе на вопросы и объяснении решения задач;
- помочь иностранным студентам овладеть методами решения задач.
Основа пособия – три главы: «Элементы линейной алгебры», «Векторная алгебра» и «Аналитическая геометрия», каждая из которых содержит необходимый теоретический материал и образцы решений типовых задач. Главы разбиты на структурные единицы – параграфы. Часть примеров взята из известных задачников Д.В. Клетеника [2], Р.Ф. Апатенок, А.М. Маркиной и В.Б. Хейман [1]. Большинство задач представляет собой авторские разработки. В конце каждого раздела имеется блок теоретических вопросов и задания для самостоятельного решения, которые позволят проверить освоение учебного материала. Учебное пособие начинается общим предисловием, введением и таблицами основных обозначений. В конце пособия проводятся решения и ответы к задачам, имеются заключение, список литературы, справочные приложения и глоссарий.
Структура и содержание предложенного пособия соответствуют традиционным подходам к изложению разделов математики в вузе, а также специфическим требованиям, предъявляемым к учебным материалам для иностранных студентов, проходящим обучение на неродном языке в неродной социокультурной среде. Освоенный надлежащим образом материал пособия позволяет организовать аудиторную и внеаудиторную работу иностранных студентов и будет служить им хорошей базой для успешного изучения других разделов математики и широкого спектра естественнонаучных дисциплин.
Ориентация на ограниченность словарного запаса у иностранных студентов, изучающих математику на русском языке, обуславливает в процессе подготовки учебных материалов для данного контингента учащихся необходимость тщательного отбора форматов изложения, терминов, вариантов формулировок определений, теорем, свойств и т.п. При этом приходится находить компромисс между стремлением унифицировать и упрощать лексические формы изложения материалов, относящихся к разным разделам курса, и желанием обеспечить их полноту и логическую завершенность.
Отличительная черта пособия – предложение для ряда задач нескольких способов решения. Наличие нескольких способов решения заставляет студентов вспомнить и обобщить весь изученный материал, выбрать оптимальный метод решения, реализовать их творческие возможности. Приведем пример нахождения уравнения плоскости, удовлетворяющей некоторым условиям двумя способами: используя уравнение плоскости, проходящей через точку перпендикулярно вектору, и с помощью условия компланарности трех векторов [2].
Пример. Записать уравнение плоскости, которая походит через точку А(1, 3, 5) и прямую ![]() .
.
Решение. Первый способ. Сделаем рисунок плоскости Р, уравнение которой надо найти (рис.1).
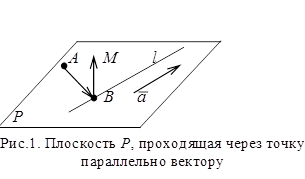
Составим уравнение плоскости, содержащей прямую ![]() , где В(1, –1, 2) – точка прямой l,
, где В(1, –1, 2) – точка прямой l, ![]() – направляющий вектор прямой l. Составим ещё два вектора
– направляющий вектор прямой l. Составим ещё два вектора![]() и
и ![]() , где M(x, y ,z) – произвольная текущая точка плоскости Р.
, где M(x, y ,z) – произвольная текущая точка плоскости Р.
Вычисляя смешанное произведение векторов ![]() ,
,![]() ,
, ![]() , запишем уравнение плоскости в векторной и координатной формах:
, запишем уравнение плоскости в векторной и координатной формах:
![]() , или
, или
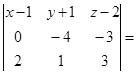
![]()
Запишем уравнение плоскости
![]() ,или
,или![]() .
.
Второй способ. Сделаем рисунок плоскости Р, уравнение которой надо найти (рис. 2).
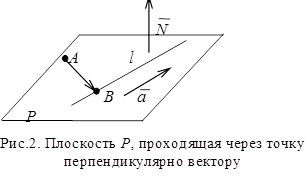
Для нахождения уравнение плоскости воспользуемся формулой
![]() ,
,
где ![]() – точка, лежащая в плоскости,
– точка, лежащая в плоскости, ![]() – нормальный вектор плоскости.
– нормальный вектор плоскости.
Координаты нормального вектора найдем по формуле
![]() ,
,
где В (1, –1, 2) – точка прямой l, ![]() – направляющий вектор прямой l.
– направляющий вектор прямой l.
Найдем координаты векторов ![]() и
и![]() :
:
![]() ;
;
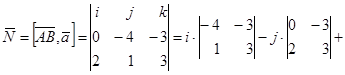
![]()
![]() .
.
Таким образом, ![]() – нормальный вектор искомой плоскости Р.
– нормальный вектор искомой плоскости Р.
Запишем уравнение плоскости
![]() ,или
,или![]() .
.
Независимо от способа решения, результаты совпали.
Таким образом, мы можем проследить взаимосвязь между разделами учебного пособия. Вычисление определителей студенты рассматривают в разделе «Линейная алгебра». К разделу «Векторная алгебра» относится нахождение координат векторов и вычисление векторного и смешанного произведения. Различные способы задания плоскости описываются в разделе «Аналитическая геометрия». Использование рисунка делает наглядным условие задачи и помогает выбрать способ решения. Описание хода решения позволяет активизировать лексический запас иностранных студентов при ответе на вопросы и объяснении решения других задач как математических дисциплин, так и профессионального профиля.
Отличительными элементами пособия, предназначенного для студентов, которые изучают математику на неродном языке, являются глоссарий и лексический минимум. Студент имеет возможность обратиться к ним на любом этапе освоения дисциплины. Глоссарий состоит из терминов, которые студентам необходимо усвоить в процессе изучения материала. Лексический минимум содержит наиболее часто встречающуюся в пособии лексику, знание которой необходимо иностранному студенту для чтения текста, для ответов на вопросы и для освоения профессиональных дисциплин в будущем.
Задания для самостоятельного решения по каждой теме играют важную роль в освоении теоретического материала. Студент может выполнять их в процессе подготовки к занятию, непосредственно на самом занятии под руководством преподавателя или в качестве домашнего задания для закрепления учебного материала.
Прочтение текста, разбор примеров, ответы на вопросы – это составляющие самостоятельной внеаудиторной работы студентов по подготовке к работе в аудитории. Таким образом, реализуется принцип опережающего обучения, и на занятиях можно расширять и углублять понимание изучаемого материала. Разработка специальных учебных пособий может стать одним из условий решения методических проблем и позволит более эффективно организовать аудиторную и внеаудиторную работу иностранных студентов, формировать их академическую адаптацию.
В заключение отметим, что учебное пособие:
- соответствует рабочей программе дисциплины;
- рассчитано на аудиторию иностранных студентов;
- включает в себя комплекс заданий, позволяющих организовать весь цикл обучения дисциплине;
- является одним из условий эффективной работы по подготовке иностранных студентов к профессиональной деятельности;
- является инструментом их академической адаптации.
Каждый студент в ходе обучения выбирает индивидуальную траекторию для самостоятельной работы и может воспользоваться материалами при ликвидации пробелов в той или иной области знаний. Организация самостоятельной работы студентов и создание учебно-методического комплекса дисциплины призваны реализовать личностно-ориентированный подход в обучении и определить результат качественного образования.
Рецензенты:
Рожкова С.В., д.ф.-м.н., профессор Томского политехнического университета, г. Томск.
Килин В.А., д.ф.-м.н., профессор Томского политехнического университета, г. Томск.



