Введение
Освоение морских территорий требует эффективных методов обнаружения подводных технических объектов. Решающая роль в обнаружении отводится пассивной гидроакустике, основанной на совокупном применении гидрофонов, как стационарных, так и подвижных.
Основным признаком присутствия подводного технического объекта в акватории является типичная для данного класса акустическая шумовая сигнатура, сильно изменяющаяся как от параметров морской среды, так и от характера перемещения объекта. Частотная и пространственная неоднородность затухания звука в морской среде, снижение заметности современных подводных технических объектов, а также медленное изменение сигнала, связанное с низкой скоростью перемещения, крайне затрудняют задачу оперативного обнаружения классическим способом превышения порога при минимальном накоплении информации [1]. Это вынуждает использовать дополнительные признаки присутствия объекта в наблюдаемом сигнале, например уровень дисперсии и показатель скорости увеличения интенсивности сигнала [2]. Для совокупного принятия решения на основе анализа нескольких признаков необходим математический аппарат и инструментальная программная среда. В работе для решения задачи обнаружения по интенсивности гидроакустического шума был использован алгоритм на основе нечеткой логики в совокупности с методами цифровой обработки сигнала.
Описание системы
В работе за основу была принята типовая многоканальная система пассивной гидролокации, состоящая из ненаправленных автономных гидрофонов, где сигнал передается по радиоэфиру на единый блок обработки информации и принятия решения об обнаружении.
Входные данные для такой системы представляют собой потоки акустического сигнала, вызванного гидростатическим давлением в гидрофоне, размещенном в заданной части акватории. Первичная обработка информации включает в себя методы цифровой обработки сигналов, такие как фильтрация, преобразование Фурье, методы свертки и взаимных корреляционных вычислений. Далее результат обработки поступает на вход порогового устройства, где принимается решение об обнаружении среди шума сигнала от технического объекта на основе выбранного уровня порога в соответствии с характеристиками вероятности ложной тревоги и правильного обнаружения. Как правило, уровень порога устанавливается на двукратном превышении амплитуды сигнала над шумом. Решение задачи локации путем триангуляции требует одновременного обнаружения сигнала тремя датчиками, при этом уровень мощности каждого обнаруженного акустического сигнала необходимо перевести в расстояние до объекта. На практике используется приближенная формула зависимости расстояния от уровня мощности сигнала, что вносит погрешность в определение расстояния от датчика до объекта.
Таким образом, в оценке местоположения объекта типовой системой пассивной гидролокации используется информация только с датчиков, где пороговое устройство зафиксировало необходимое превышение уровня сигнала, остальные датчики не участвуют в анализе.
Авторами предложен иной подход к задаче обнаружения [3-4]. Вместо порогового принятия решения используется аппарат нечеткого вывода на основе анализа двух критериев: мощность сигнала в заданном участке спектра и характер изменения сигнала во времени. В результате на выходе системы обнаружения для каждого датчика возвращается степень истинности присутствия технического объекта (далее СИП), которая может принимать значения от 0 до 1. Таким образом, в анализе местоположения объекта участвует информация со всех датчиков, но со своей степенью истинности. Например, каналу, в котором явно отсутствует полезный сигнал, соответствует нулевая степень истинности.
В рамках данного подхода возникла необходимость отобразить на карте единую суммированную информацию с датчиков в виде двумерного распределения степеней истинности присутствия.
Описание решения
В каждый момент времени на вход системы с датчиков поступает информация, которая после обработки обозначается как нормированная мощность полезного сигнала (Ei) в точке приема i-м датчиком.
Для начала установим зависимость расстояния до объекта (r) от мощности полезного сигнала в точке приема (E) в соответствии с законом затухания в степени 3/2:
![]()
Далее установим закон спада СИП объекта в зависимости от предполагаемого местоположения. Для этого используем формулу закона нормального распределения плотности вероятности с домножением на уровень мощности E:
![]() , (2),
, (2),
где ![]() – коэффициент «размазанности»,
– коэффициент «размазанности»,
![]() – расстояние от какой-либо точки карты Z(x,y) до точки датчика Di(xd;yd).
– расстояние от какой-либо точки карты Z(x,y) до точки датчика Di(xd;yd).
Максимум функции соответствует предполагаемому расстоянию объекта от датчика, а абсолютное значение равно уровню мощности в точке приема датчиком. Таким образом, с увеличением предполагаемого расстояния до объекта увеличивается и размазанность функции СИП (рис. 1).
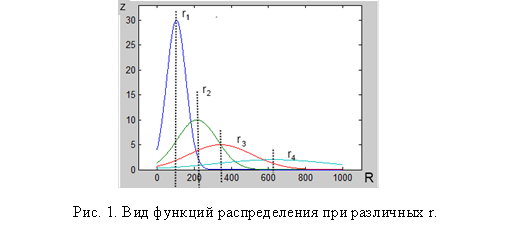
Решение задачи отображения карты для одного датчика сводится к вычислению степени истинности для каждой точки карты Z(x,y) исходя из рассчитанного удаления этой точки от датчика R и заданного в начальных условиях r.
В результате получим карту распределения истинности присутствия, где максимальный уровень истинности сосредоточен на окружности с радиусом r (рис. 2).
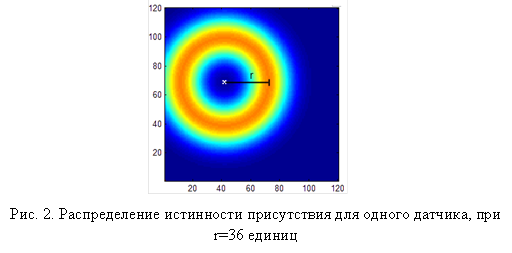
На следующем этапе выполняется матричное суммирование значений СИП для всех датчиков, участвующих в анализе. В результате получаем единую карту, на которой яркому пятну (цвет ближе к красному) соответствует зона с максимальной степенью истинности присутствия объекта в данный такт моделирования.
Моделирование проводилось в программной среде MATLAB, где для вывода на экран содержимого двумерного массива использовалась функция «imagesc()» с автоматическим масштабированием по цветовой карте «jet».
Динамика изменений карты СИП при движении объекта по прямолинейной траектории мимо четырех датчиков показана на рисунке 3, для наглядности датчики расположены не на одной прямой.
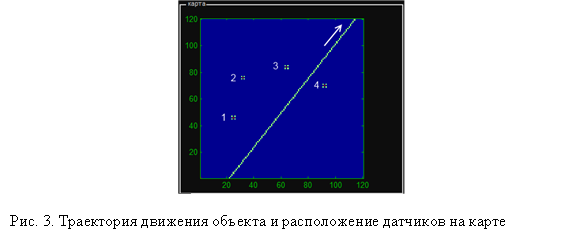
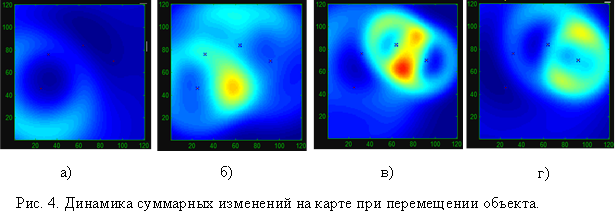
Зонам, обозначенным цветом ближе к синему (по цветовой карте «jet»), соответствует минимальное значение функции СИП объекта. Отметим особенности данного способа отображения.
1. Датчики, находящиеся на значительном удалении от объекта, вносят минимальный вклад в решающее значение функции.
2. По мере приближения объекта к нескольким датчикам уменьшается площадь зоны максимальных значений функции СИП объекта.
3. В случае когда объект находится между двумя датчиками на близком расстоянии (рис. 4в), удаленные датчики вносят решающий вклад в выбор «более истинного» местоположения объекта.
4. Отсутствует необходимость принудительного округления данных при указании координат.
Для проверки работы данной модели на реальном сигнале требуется указать входные параметры, такие как координаты датчиков, шумность объекта и зависимость расстояния от интенсивности шума, получаемого датчиком. Работа с реальными данными, а также выбор оптимальных параметров обработки сигнала является предметом дальнейшей работы.
Рецензенты:
Игнатюк В.А., д.т.н., профессор кафедры электроники, Владивостокский государственный университет экономики и сервиса, г. Владивосток.
Павлов А.Б., д.ф.-м.н., заведующий лабораторией, Институт автоматики и процессов управления, г. Владивосток.



