В настоящее время в распределенных моделях формирования весеннего стока расчеты интенсивности снеготаяния выполняются по уравнению теплового баланса снежного покрова (в предположении, что температура тающего снега равна 0°) [9]; по среднесуточной температуре воздуха (обычно для расчета стока с водосборов горных рек, слабо освещенных сетью наблюдений) [2]; или на основе эмпирических формул, связывающих элементы теплового баланса снежного покрова с метеорологическими параметрами [6].
Выбор метода для расчета снеготаяния определяется имеющимися исходными данными, изученностью водосбора, плотностью и репрезентативностью наблюдательной сети. В любом случае одной из основных проблем при моделировании является корректное восстановление входных полей метеоэлементов, с учетом их пространственной неоднородности, обусловленной особенностями рельефа и растительного покрова.
В настоящей статье рассмотрены методы восстановления входных полей метеоэлементов, для распределенного моделирования процесса снеготаяния по методу теплового баланса. Также проанализированы результаты расчетов снеготаяния с применением различных методов. Подготовка исходных данных и расчеты выполнены средствами программных продуктов ArcGis 10.1, Scanex Image Processor v. 3.6.9, и SAGA 2.0.
В качестве входных данных в моделях снеготаяния используются цифровые модели рельефа; карты типизации растительного покрова; данные о максимальном запасе воды в снежном покрове; ежедневные данные наблюдений на сети метеостанций в период снеготаяния; данные ДЗЗ низкого и среднего разрешения – для калибровки модели и проверки результатов. В зависимости от выбора метода расчета интенсивности снеготаяния используется различный набор входных метеорологических данных.
Расчет снеготаяния по тепловому балансу обеспечивает, в большинстве случаев, наиболее высокую точность [4]. Решение уравнения теплового баланса строгими методами предполагает наличие комплекса наблюдений, который возможно осуществить лишь на экспериментальных водосборах и воднобалансовых площадках. Поэтому в чистом виде метод теплового баланса на практике не применяется. Для оценки составляющих теплового баланса П.П. Кузьминым разработаны упрощенные эмпирические способы [4]. Они позволяют определить радиационную и адвективную составляющую снеготаяния, а также испарение с поверхности снежного покрова, при использовании только данных стандартных наблюдений за температурой и влажностью воздуха, облачностью, осадками и ветром.
С использованием предложенных П.П. Кузьминым эмпирических формул для расчета теплового баланса снежного покрова нами выполнен расчет интенсивности снеготаяния за весенний период 2011-2012 гг. Период расчета в 2011 г. – с 4 апреля по 10 мая, в 2012 г. – с 30 марта по 25 апреля. Территория исследования – водосбор Воткинского водохранилища.
В качестве ЦМР водосбора использована глобальная модель рельефа Etopo2 (GLOBE), с пространственным разрешением 30 угловых секунд. Для получения актуальных данных о типах растительного покрова на водосборе Воткинского водохранилища была создана карта типизации подстилающей поверхности (LandCover), с пространственным разрешением 250 м, на основе разносезонных данных со спутника Terra MODIS (за 2010 и 2011 гг.).
Восстановление максимального запаса воды в снежном покрове выполнено на основе данных снегомерных съемок. Интерполяция снегозапаса по данным снегомерных съемок выполнялась по методу, предложенному В.А. Шутовым [7], раздельно для леса и поля, с учетом зависимостей снегозапасов от высоты местности, и поправочных коэффициентов на тип растительного покрова (предложенных в работе [7]). Изменчивость снегозапасов, связанная с перераспределением снега на мезо- и микрорельефе, метелевым переносом, учитывается с помощью кривой распределения снегозапасов. Вертикальный градиент запасов воды в снеге принят равным 15%/100 м в нижних высотных поясах и 10% в верхних, что соответствует данным, приведенным в работе [1].
Расчет снеготаяния по методу П.П. Кузьмина позволяет выделить радиационную и адвективную составляющие снеготаяния, а также учесть испарение со снежного покрова. Уравнение теплового баланса снежного покрова, без учета его второстепенных составляющих, записывается следующим образом:
W = WР + WК + WИ (1)
где WР - радиационный баланс, WК - турбулентный поток тепла, WИ - поток тепла на испарение снега.
Радиационная составляющая снеготаяния (MR) рассчитывается по уравнению:
MR =Qsw – Qls + Qlw , (2)
где Qsw – баланс коротковолновой радиации, Qls – эффективное излучение снега, Qlw – встречное излучение атмосферы. Составляющие радиационного баланса определяются по формулам (3-5):
Qsw = 0,125(Q + q)(1 – R)(1 – 0,2No – 0,47Nn) – Qls + Qlw , (3)
Qls = k(e×s×T04) , (4)
Qlw= k(e×s×T04)(0,62+0,05(E200))0,5)(1+0,12 No +0,12 Nn) , (5)
где Q+q – суточная сумма прямой и рассеянной радиации (без учета облачности), R – альбедо снежного покрова, No и Nn – общая и нижняя облачность в %, T0 – абсолютная температура воздуха, E200 – парциальное давление водяного пара на высоте 2 м, s - постоянная Стефана-Больцмана (8.16×10-11 кал/(см2×мин×К4)), e - относительная излучательная способность снега в тепловом диапазоне, принятая равной 0,99 [4].
Расчет радиационного баланса снежного покрова в лесу представляет собой крайне сложную задачу, поскольку он теснейшим образом связан с характером самого леса. Кроме того, в лесу значимым источником энергии снеготаяния является поступление длинноволновой радиации от стволов и крон деревьев. В работе П.П. Кузьмина [4] приведены зависимости интенсивности снеготаяния в лесу от породного состава и полноты насаждения. В данной работе для расчета радиационной составляющей снеготаяния в лесу были использованы полученные на основе этих зависимостей коэффициенты в предположении, что среднее значение полноты насаждений составляет 0,7. Для темнохвойного леса данный коэффициент принят равным 0,33, для мелколиственного леса 0,6, для соснового леса 0,4. В ночные часы, радиационная составляющая снеготаяния принималась равной нулю.
Адвективная составляющая снеготаяния определяется турбулентным теплообменом снежного покрова с атмосферой и притоком тепла вследствие конденсации водяного пара на поверхности снега:
Ma = k(1+0.544×U10)(q2 – q0 + 1,75(Е2 – Е0)), (6)
где U10 – скорость ветра на высоте 10 метров, q2 и Е2 – температура воздуха и парциальное давление водяного пара на высоте 2 м, q0 – температура поверхности снежного покрова, Е0 - максимальная упругость водяного пара по температуре поверхности снега.
Коэффициент k перед формулой (6) зависит от временного шага модели, при расчете с шагом 12 ч. он принимается равным 0,434.
Испарение с поверхности снежного покрова вычисляется по формуле Кузьмина [4]:
E = 0,18 +0,098×U10(Е2 – Е0) . (7)
Восстановление входных полей метеоэлементов для расчета теплового баланса снежного покрова за каждый день периода снеготаяния выполнялось средствами ГИС-технологий на основе методов, предложенных в работах С.Г. Яковченко и Шутова [7; 8].
Расчет суммарной солнечной радиации (по цифровой модели рельефа и широте местности, без учета облачности) является стандартной функцией многих ГИС. Для решения этой задачи нами использована ГИС SAGA (System for Automatized Geoscientific Analysis). Поправки на облачность были введены по формуле (3). Общая и нижняя облачность интерполировалась по данным сети метеостанций.
Альбедо снежного покрова вычислялось по эмпирической формуле, предложенной авторами гидрологической модели DHVSM [10].
![]() , (8)
, (8)
где 0,9 – альбедо свежевыпавшего снега, λ – параметр, принимаемый равным 0,85.
Альбедо снега является весьма изменчивой величиной, и достоверность его оценки при отсутствии инструментальных наблюдений в значительной мере определяет точность расчета интенсивности снеготаяния.
Поле температуры воздуха восстанавливалось на основе данных наблюдений 34-х метеостанций (расположенных как в пределах исследуемого водосбора, так и за его границами), с учетом вертикального градиента температуры, который оценивался по данным радиозондирования атмосферы. Альтернативным вариантом является вычисление вертикального градиента температуры на основе выходных данных глобальной численной модели прогноза погоды GFS/NCEP (с пространственным разрешением 0,5° и временным разрешением 6 ч). Данные GFS/NCEP были получены в формате Grib2 и конвертировались в формат ГИС с помощью программы tkDegrib.
Поле влажности воздуха (парциального давления водяного пара) имеет меньшую связность, чем поле температуры. Для его восстановления использовалась следующая методика: влажность воздуха интерполировалась по данным метеостанций, на основе данных модели GFS/NCEP определялась влажность на изобарической поверхности 900 гПа. Далее восстанавливалось поле влажности воздуха с учетом ее вертикального градиента.
Поле скорости ветра восстанавливалось по данным модели GFS/NCEP и далее корректировалось с учетом рельефа местности и типов растительного покрова. Для коррекции на высоту местности использована эмпирическая зависимость скорости ветра от высоты, в которой коэффициент K принимается равным 0,25:
V1 = V0(H1/H0)k, (9)
где H1 – высота местности, H0 – высота ближайшей метеостанции, V0 – скорость ветра на метеостанции.
Чтобы учесть снижение скорости ветра в лесу, были введены специальные поправочные коэффициенты: для темнохвойного леса – 0,15; для смешанного леса 0,2; для мелколиственного леса 0,25. Аналогичные значения поправок приведены в работе [3].
Температура поверхности снежного покрова q0 = 0°, если температура воздуха q2 ≥0. Если q2 < 0°, то q0 = q2.
Максимальная упругость водяного пара по температуре поверхности снега Е0 = 6,11 гПа, если q2≥0. Если q2<0, то Е2 = Е0.
На рис. 1 приведены примеры результатов расчета радиационной и адвективной составляющих снеготаяния и испарения со снежного покрова, за сутки 08.04.2012 г.
Осадки в период снеготаяния интерполировались с учетом вертикального градиента, принятого равным 10%/100 м высоты.
Вычисленные величины интенсивности снеготаяния и испарения суммировались за суточные интервалы времени, и дальнейший расчет площади снежного покрова, водоотдачи и остаточного снегозапаса выполнялся с суточным шагом. Площадь снежного покрова определялась по методу А.Г. Ковзеля на основе модульных коэффициентов и кривых распределения снегозапаса. Параметры кривых распределения для лесной и безлесной части территории получены из работы [5]. Для озер и водохранилищ задано равномерное распределение снегозапаса. Водоотдача снежного покрова рассчитывается по методике [5], с учетом водоудерживающей способности снега, которая принимается равной для леса – 20%, для поля – 15%. Также учитывается снижение влагоемкости снега за счет выпадения жидких осадков. При расчете поступления талых вод на водосборы учитываются жидкие и твердые осадки, формирование и таяние временного снежного покрова. Пример результатов расчета динамики запаса воды в снеге с шагом 5 суток (за 2011 год) показан на рис. 2.
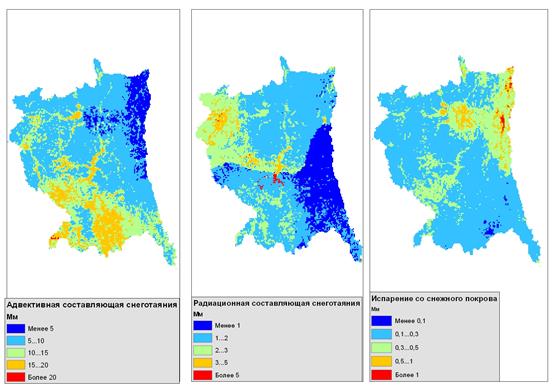
Рис. 1. Результаты расчета составляющих снеготаяния и испарения за сутки 08.04.2012 г.
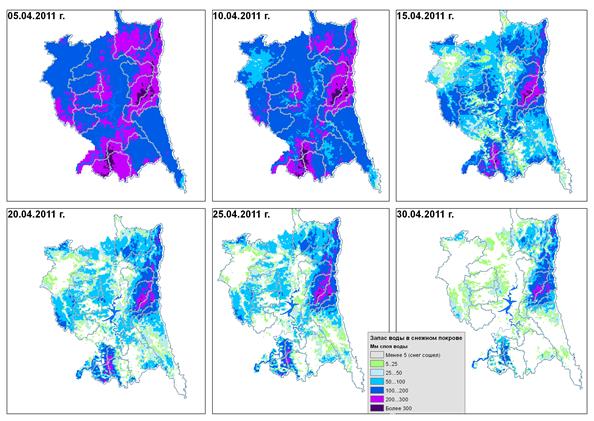
Рис. 2. Динамика процесса снеготаяния в 2011 г. на водосборе Воткинского вдхр.
Обсуждение результатов
Валидация расчетной площади снежного покрова проводилась на основе космических снимков низкого и среднего разрешения. Валидация результатов расчета запаса воды в снеге выполнена по данным снегомерных съемок. Кроме того, результаты расчетов по вышеописанной методике были сопоставлены с результатами, полученными по упрощенному варианту модели, в котором интенсивность снеготаяния в пределах безлесной территории рассчитывались на основе формул Е.Г. Попова, а в лесу – по температурным коэффициентам стаивания. На рис. 3 приведено сопоставление расчетной и фактической (со снимку LANDSAT-5) заснеженности территории (на 04.05.2011 г.). На рис. 4. показано распределение ошибок расчетного запаса воды в снеге за 2011 год. На рис. 5 приведено сопоставление запаса воды в снежном покрове, рассчитанного с использованием двух разных методов, для водосборов рек Яйва, Коса и Ирень.
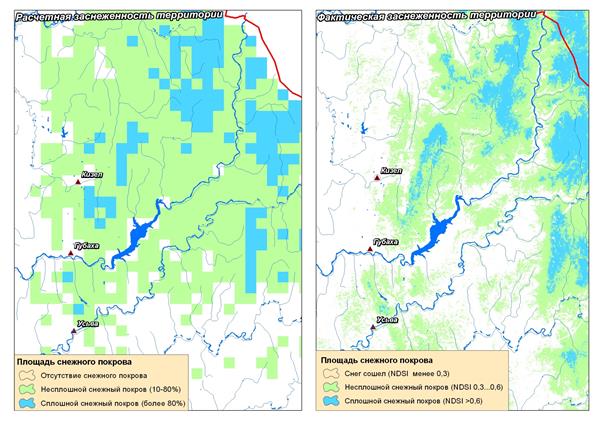
Рис. 3. Сопоставление фактической и расчетной заснеженности территории
Результаты расчета по методу П.П. Кузьмина за 2011 год являются в целом достоверными. На это указывает как хорошая сходимость расчетной и фактической площади заснеженности, так и распределение ошибок расчетного снегозапаса. Ошибки имеют в основном случайный характер, они связаны с локальными особенностями участков снегомерных съемок. Систематическое занижение расчетного снегозапаса наблюдается лишь на севере территории.
Результаты расчетов за 2012 год характеризуются систематическим завышением интенсивности снеготаяния (рис. 5). В наибольшей степени оно проявляется в начале второй декады апреля. Поскольку результаты расчета по методу Е.Г. Попова и по среднесуточной температуре воздуха также характеризуются некоторым систематическим завышением интенсивности снеготаяния, ошибки расчета по методу П.П. Кузьмина оказываются весьма значительными.
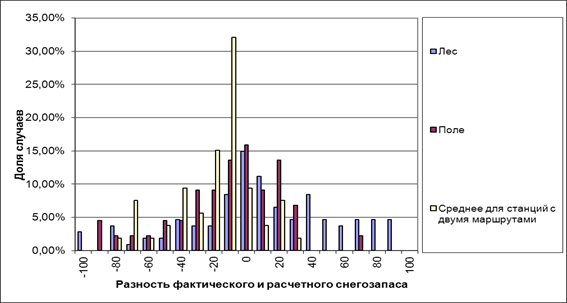
Рис. 4. Распределение ошибок расчетного запаса воды в снежном покрове (2011 год)
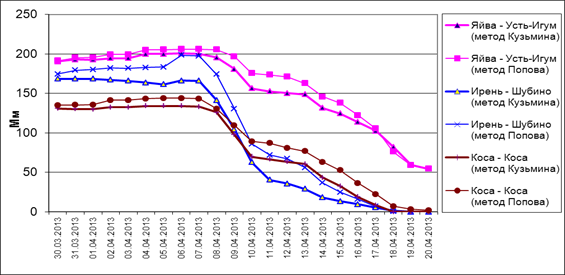
Рис. 5. Сопоставление запаса воды в снежном покрове, рассчитанного по методу П.П. Кузьмина (1) и по методу Е.Г. Попова (2) в апреле 2012 г.
Основными причинами систематического завышения интенсивности снеготаяния, рассчитанной по методу П.П. Кузьмина, в 2012 г. являются низкая точность оценки альбедо снежного покрова и некоторое завышение адвективной составляющей интенсивности снеготаяния в условиях высокой влажности воздуха (10-12 апреля). Именно в этот период сформировались значительные отклонения расчетного запаса воды в снеге и площади заснеженности, рассчитанной по разным методам. В то же время стоит отметить и некоторые значительные преимущества метода П.П. Кузьмина для расчета снеготаяния – его физическую обоснованность, применимость в широком спектре климатических условий, более высокую точность расчета в условиях преобладания «радиационного» типа снеготаяния. В обоих случаях ошибки при расчете снеготаяния связаны в значительной степени с низкой точностью оценки максимального снегозапаса на отдельных участках исследуемой территории.
Исследование выполнено в рамках реализации федеральной целевой программы «Научные и научно-педагогические кадры инновационной России» на 2009 – 2013 годы, в ходе выполнения работ по Соглашению № 14.B37.21.18, а также при поддержке гранта РФФИ (проект № 11-05-96026-р_урал_а).
Рецензенты:
Калинин Н.А., д.г.н., профессор, зав. кафедрой метеорологии и охраны атмосферы ПГНИУ, г. Пермь.
Калинин В.Г., д.г.н, профессор кафедры физической географии и ландшафтной экологии ПГНИУ, г. Пермь.



