В статье рассмотрен процесс развития математической речи школьников в процессе изучения определений понятий, теорем, правил в соответствии с деятельностным, личностно-ориентированным подходом и теорией поэтапного формирования умственных действий.
В последние годы происходят существенные изменения в российском образовании. В частности, осуществляется внедрение нового федерального государственного образовательного стандарта [5].
Стратегическая цель стандарта состоит в формировании умения «учиться». Для её достижения ученик должен овладевать основными действиями, составляющими основу этой деятельности – универсальными учебными действиями (УУД): личностными, метапредметными, предметными.
Необходимым условием формирования всей системы универсальных и предметных (математических) действий является развитие математической речи школьников. Новый стандарт основного общего школьного образования рассматривает речь как необходимый компонент личностных, метапредметных и предметных результатов обучения. В частности, отмечается необходимость усвоения школьниками математического языка и математической речи, выделяется знание языка алгебры, геометрии, а также умение точно и грамотно выражать свои мысли в устной и письменной речи как необходимый компонент предметных результатов обучения.
Проблеме развития математической речи школьников уделялось значительное внимание в теории и методике обучения математике (В.В. Репьёв [6], И.А. Гибш [1], Б.В. Гнеденко [2], А.Я. Хинчин [7] и др.). Однако в этих работах речь шла, во-первых, о важности развития речи школьников; во-вторых, давалась характеристика грамотной математической речи; в-третьих, основным условием развития математической речи школьников считалась безупречная математическая речь учителя математики, которая служила бы образцом речи учеников. В рассмотренных работах недостаточно внимания уделялось непосредственно ученику как субъекту учебной деятельности.
В опубликованных нами ранее работах [3] были выявлены условия развития математической речи школьников. Кратко изложим их. Основное условие развития речи в целом, и не только математической, состоит в том, чтобы ученик включался в «процесс говорения». При этом следует помнить, что в психологии различают два вида речи: внешнюю и внутреннюю. Последняя формулируется на основе внешней. Наиболее значимой при этом является семантическая сторона внутренней речи. В сознании человека слова нагружаются смыслом, результатом чего является идиоматичность словесных значений, их непереводимость на язык внешней речи, понятность только самому говорящему.
Перевод внешней речи во внутреннюю (интериоризация) сопровождается редуцированием (сокращением) структуры внешней речи, а переход от внутренней речи к внешней (экстериоризация) требует, наоборот, развертывания структуры внутренней речи, построения ее в соответствии не только с логическими, но и грамматическими правилами. Интериоризация невозможна без понимания смысла речи. Процесс экстериоризации требует создания высказывания, соответствующего требованиям, предъявляемым к математическим предложениям.
Далее, согласно Л. С. Выготскому, речь ребёнка напрямую связана с уровнем развития его мышления, обусловлена им и обуславливает его, т.е. процессы формирования мышления и речи неразделимы, поэтому следует говорить не о развитии речи, а о становлении речевого мышления.
Следовательно, развитие речи невозможно без изучения математического языка, используемого речью для передачи информации. Поэтому в целом в речевом мышлении между речью, мышлением и языком происходят очень сложные, глубокие связи. Условно их взаимодействие можно представить в виде следующей схемы:

Рис.1. Взаимосвязь мышления, речи и языка
Связующим звеном между мышлением, языком и речью выступает понимание смысла передаваемого содержания, которое, в свою очередь, невозможно без осознания говорящим логических конструкций определения математических понятий, формулировок теорем, методов доказательств, построения силлогизмов.
В психологии доказано, что развитие личности в целом и мышления в частности происходит в деятельности. Важно, чтобы ученик был субъектом учебной деятельности на всех её этапах: мотивационно-ориентировочном, операционно-познавательном, рефлексивно-оценочном. Включение ребёнка в деятельность в соответствии с психологической структурой учебной деятельности необходимо актуализирует как его внутреннюю, так и внешнюю речь, способствует осознанию смысла предстоящей деятельности, пониманию производимых им и учителем действий на уроке.
Поэтому методологической основой развития математической речи школьников является деятельностный и личностно-ориентированный подходы. Личностно-ориентированное обучение предполагает создание таких условий, в которых ученик «может» и «хочет» учиться. В этом случае деятельность на уроке будет иметь для ученика «личностный смысл». В свою очередь, наличие личностного смысла способствует превращению предметного (объективного) знания в личностное знание ученика.
Личностное знание отражает сплав личных потребностей, личностного смысла и объективного предметного знания. Личностное знание связано с потребностью ученика в получении нового для него знания, с процессом познания, в котором он является активным участником получения нового знания.
Личностно-ориентированное обучение сопровождается осознанием, рефлексией учеником, во-первых, своей деятельности. Во-вторых, оценкой полученных новых знаний и способов деятельности, прогнозированием их применения.
Поэтому из вышесказанного следует, что необходимыми условиями развития математической речи школьников являются владение математическим языком и математической символикой, логической составляющей математической деятельности.
Развитие математической речи школьников происходит на всех этапах процесса обучения. Наиболее важным из них является этап получения новых знаний. В частности, это связано с тем, что, во-первых, мышление содержательно. Построение любых математических высказываний учениками должно, в первую очередь, опираться на изученный ими материал, без чего речь не может стать полноценной.
Во-вторых, при этом ученик овладевает новой терминологией и математическим языком, что является важным условием развития математической речи, поскольку владение терминологией и математическим языком даёт возможность ученику понимать то, что говорит учитель, ученики, а также то, что написано в математической литературе.
В-третьих, при этом ученик овладевает логической структурой математических понятий, теорем, структурой вероятностных и дедуктивных умозаключений.
Поэтому далее опишем технологию обучения основным дидактическим единицам, которая удовлетворяла бы описанным выше условиям развития математической речи школьников. Из известных нам технологий обучения основным дидактическим единицам наиболее адекватной нам представляется технология, описанная в работе [4]. Она разработана в соответствии с деятельностным и личностно-ориентированным подходами и носит развивающий характер. Однако, поскольку в ней акцент на развитие математической речи специально не ставился, то мы её модифицируем. В методологическое основание описанной выше технологии мы добавляем теорию поэтапного формирования умственных действий П.Я. Гальперина – Н.Ф. Талызиной.
Суть этой технологии в очень упрощённом варианте состоит в формировании умственных действий на основе создания ориентировочной основы действий (ООД):
1) создание ООД – модели умственного предметного действия, адекватного соответствующей дидактической единице;
2) усвоение выделенных умственных действий в соответствии с выделенными этапами.
- этап формулирования цели предстоящей деятельности;
- этап выполнения действия во внешнеречевой форме;
- этап формирования действия как внешнеречевого;
- этап формирования действия во внутренней речи про себя;
- этап формирования действия во внутренней речи.
Согласно теории поэтапного формирования умственных действий П.Я. Гальперина – Н.Ф. Талызиной, наиболее благоприятным для развития внутренней и внешней речи является процесс усвоения учеником умственного предметного действия. В нашем случае, предметные учебные действия состоят в действиях по оперированию изученными определениями математических понятий, теорем, правил, которые являются содержательной базой ООД.
Поэтому для нас важно модифицировать эту теорию так, чтобы вначале ученик выявлял в совместной деятельности с учителем содержательный аспект ООД.
В свете нашей проблемы и учитывая вышесказанное, технология изучения основных дидактических единиц должна включать:
1. Выявление учеником как субъектом учебной деятельности содержательной основы умственного предметного действия.
2. Создание ориентировочной основы действия, адекватного выявленному содержанию (соответствующей дидактической единице).
3. Усвоение умственного действия, формирование умения оперировать определениями математических понятий, теоремами, правилами.
Таким образом, целостная технология изучения дидактических единиц, способствующая развитию внешней и внутренней математической речи школьников, строится в соответствии с психологической структурой учебной деятельности в единстве развития мышления и речи следующим образом:
- Мотивационно-ориентировочная часть может состоять из четырех взаимосвязанных звеньев (этапов): актуализации, мотивации, постановки учебной задачи (вычленение проблемы), планирования ее решения.
Цель этапа актуализации состоит не только в повторении опорных знаний, но и в осмыслении учеником предыдущей деятельности. В систему упражнений на этом этапе важно включать такие, которые внешне сходны с теми, которые ученики могли только что решить, но фактически для их решения не хватает имеющихся знаний или способов действий. Таким образом, этап актуализации плавно переходит в этап создания мотивации дальнейшей деятельности.
Цель этапа мотивации заключается в формировании у каждого учащегося личной потребности в последующей деятельности, связанной с открытием субъективно нового для него содержания. Известно, что деятельности без мотива не бывает. Мотив является внутренней побудительной причиной к действию, желанием удовлетворить какую-либо потребность. Правильно организованные этапы актуализации и мотивации призваны вызвать у ученика чувство уверенности – «могу», и желания – «хочу», что соответствует личностно-ориентированному обучению.
Этап мотивации естественно переходит в этап вычленения проблемы и постановки учебной задачи (цели) урока.
Цель этапа планирования состоит в проектировании программы дальнейшей деятельности. На этом этапе ученики прогнозируют последовательность действий, ведущих к достижению поставленных целей.
Итак, основная функция мотивационно-ориентировочной части носит смыслообразующий характер.
Операционно-познавательная часть учебной деятельности направлена непосредственно на решение учебной задачи. На уроках изучения нового материала она проектируется в соответствии со спецификой поисковой математической деятельности, которая конкретизируется в технологическом процессе изучения определений математических понятий, теорем, правил.
Так, процесс открытия нового понятия может происходить следующим образом:
- выявление в совместной деятельности учителя и учащихся содержания (характеристических свойств) понятия. Здесь могут быть использованы различные приемы и формы работы, в том числе и групповая;
- «присвоение» термина (имени) новому понятию;
- конструирование определения (на основе выделенных характеристических свойств это пытаются сделать ученики);
- создание ООД – модели умственных действий по оперированию определением.
Работа с теоремой может быть организована так:
- поиск новых фактов (на основе эмпирических и гипотетико-дедуктивных методов, представленных в схеме 1);
- формулирование теоремы;
- поиск доказательства теоремы;
- оформление доказательства;
- создание ООД – модели умственных действий по оперированию теоремой.
А вот технология работы на уроке по «открытию» нового правила:
- решается специально подобранная (типичная для будущего способа) задача (или несколько таких задач);
- проводится анализ ее условия с целью выделения общего (например, решали на координатной прямой две задачи на сложение двух чисел с разными знаками);
- анализируется решение каждой задачи с целью выявления обобщенного способа (при этом очень важна логика, последовательность вопросов и заданий учителя);
- формулируется учениками правило в форме алгоритма;
- создается модель (словесная, графическая, символическая и т.д.) обобщенного способа.
Организованная таким образом основная часть урока позволяет включать учеников в речевые ситуации, в которых ученик может активно говорить, при этом оказывается задействована как его внешняя речь (и устная, и письменная), так и внутренняя речь.
Рефлексивно-оценочная часть урока включает в себя два основных аспекта: личностный и содержательный.
Личностный аспект предполагает в первую очередь осмысление и оценивание учеником своей деятельности.
Содержательный аспект предполагает осознание и осмысление учеником результата решения учебной задачи и процесса его получения, анализ методов, приемов, теоретических положений, прогнозирование применения новых знаний, преобразование теоретических знаний в способы деятельности и выделение в связи с этим эвристик (частных или общих).
На этом этапе происходит овладение учеником умственными предметными действиями по оперированию новыми знаниями в соответствии с полученной ранее моделью ООД. С точки зрения психологии, формирование и развитие речи человека в целом невозможно без этапа рефлексии. После создания ООД (в наглядной, схематической, словесной форме, в устной речи и т.д.) идёт процесс поэтапного формирования умственных действий. В зависимости от дидактической единицы, от уровня обученности и обучаемости класса, от наличия времени на уроке, методика работы на каждом этапе в соответствии с теорией П.Я. Гальперина – Н.Ф. Талызиной может быть разной. Так, при формировании умственных действий по применению определений понятий, теорем, в качестве основного методического средства могут быть устные упражнения следующего содержания:
1) как установить, что два треугольника являются подобными на основе первого признака подобия;
2) если известно, что два треугольника подобны, как доказать, что их соответственные углы равны;
3) если известно, что два треугольника являются подобными, то, что из этого следует на основе определения;
4) как доказать, что два угла в треугольниках соответственно равны;
5) как доказать на основе первого признака подобия, что два треугольника подобны?
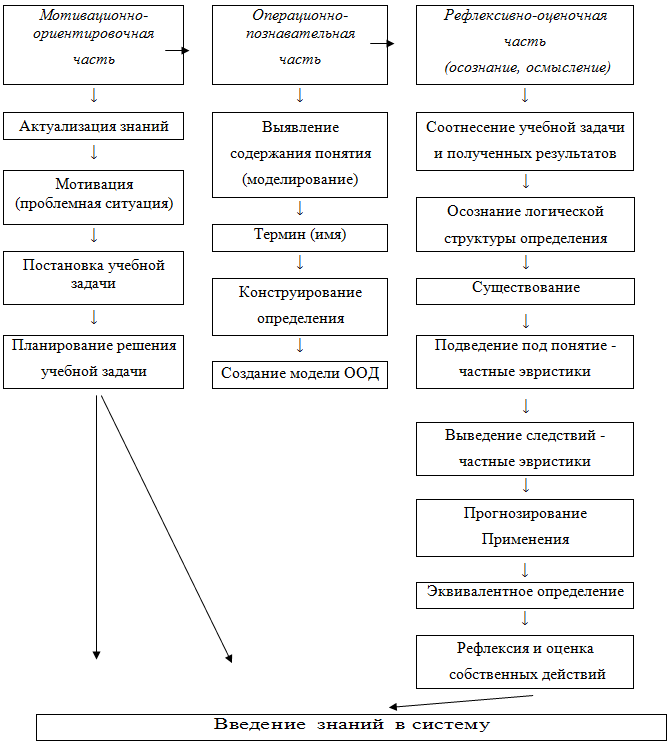
Для примера представим целостную модель технологии работы с новым понятием на уроке.
Модель технологии работы с новым понятием
В заключение сделаем несколько замечаний.
1. Описанная технология важна на начальном этапе получения учеником новых математических знаний, без овладения которыми ученик нее может включаться в другие виды деятельности.
2. Она позволяет ученику осваивать элементы учебно-исследовательской деятельности и ее методы сначала под управлением учителя.
3. Создание модели ООД осуществляется в совместной деятельности учителя и учеников. Такая модель является ориентировочной основой действия, позволяющая ученику самостоятельно формулировать эвристики для полноценной работы с определениями понятий, теоремами, правилами. Создание моделей ООД является важнейшей речевой ситуацией, в которой задействована как речь внешняя (чаще устная – в 5–7 классах, чаще письменная – в 8–11 классах), так и внутренняя.
4. В то же время эта технология, с одной стороны, инвариантна, т.к. чтобы развивать УУД, важно соблюдать все выделенные в ней этапы. С другой стороны, она вариативна, поскольку организацию каждого этапа учитель разрабатывает в соответствии с уровнем своего профессионализма, творчески.
5. Технология естественно вписывается в работу опытного учителя математики и не требует от него отказа от накопленного положительного опыта.
Рецензенты:
Перевощикова Е.Н., д.п.н., профессор кафедры общей и социальной педагогики Нижегородского государственного педагогического университета им. Козьмы Минина, г. Нижний Новгород.
Повшедная Ф.В., д.п.н., профессор кафедры общей и социальной педагогики Нижегородского государственного педагогического университета им. Козьмы Минина, г. Нижний Новгород.



