Важной составляющей риск-анализа конструкций является оценка их фактического технического состояния. В некоторых работах [1, 3-5] авторы провели анализ состояния аварийности несущих конструкций и предложили метод, который позволил сформулировать подход к оценке уровня пластической (упругой) деформации основных несущих конструкций мостовых металлургических кранов в зависимости от величины действующей нагрузки как определяющего параметра при управлении техногенной безопасностью и рисками.
Для аналитической оценки будем использовать метод вероятностного синтеза преобразования вероятностей для механической системы, в которой основными процессами, определяющими ее долговечность, являются процессы усталости и пластической и упругопластической деформации и потери устойчивости.
Определенные факторы влияют на величину пластической деформации, а именно:
Δε пр = f(εпр),
Δε σ = f(σср), (1)
Δε Кσ = f(Кσ),
где ε пр – предварительная пластическая деформация «критического объема»;
- среднее напряжение в цикле нагружения, σ ср;
- структурные особенности материала Кσ.
Внешние параметры системы будут представлять нагрузки, действующие на металлические конструкции металлургического мостового крана. В совокупности с внутренними они определяют входные параметры системы, случайным образом воздействующие на нее в виде случайного процесса «входа» системы.
Результат воздействия внешних возмущающих нагрузок и внутренних факторов определяется необратимыми изменениями в материале деталей системы, а критерии таких изменений показывают на степень повреждаемости материала при их воздействии. Очевидно, выходные параметры – это величина пластической деформации и потеря устойчивости, которая представляет собой реакцию системы на действие внешних и внутренних входных факторов.
Представим функциональную зависимость между входными и выходными параметрами системы на основании [7] в следующем виде:
Δε =![]() , (2)
, (2)
E – модуль упругости материала, n – показатель степени, определяемый экспериментально.
Решив уравнение (2) относительно ![]() , представим выражение статистической динамики с учетом [2, 3] в виде:
, представим выражение статистической динамики с учетом [2, 3] в виде:
![]() (3)
(3)
которая представляет собой плотность вероятности выходного параметра системы.
При условии независимости входных параметров по нормальному закону распределения получим функцию ![]() после решения и преобразований уравнения (3):
после решения и преобразований уравнения (3):
![]() =
= ![]() , (4)
, (4)
где ![]() – среднее значение изгибных напряжений,
– среднее значение изгибных напряжений, ![]() – среднеквадратическое отклонение изгибных напряжений.
– среднеквадратическое отклонение изгибных напряжений.
Таким образом, располагая опытными или эксплуатационными данными о предельных величинах остаточной деформации и построив кривую плотности вероятности ![]() , можно судить о возможных величинах выходных параметров для режима нагружения и требуемого срока эксплуатации. Это можно установить также при наличии статистических характеристик распределения – математического ожидания M[
, можно судить о возможных величинах выходных параметров для режима нагружения и требуемого срока эксплуатации. Это можно установить также при наличии статистических характеристик распределения – математического ожидания M[![]() ] и дисперсии D[
] и дисперсии D[![]() ], которые определяются следующими выражениями:
], которые определяются следующими выражениями:
![]() , (5)
, (5)
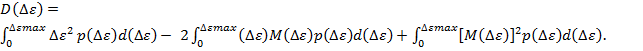 (6)
(6)
Для прогнозирующего расчета интегральная функция распределения ![]() является очень важным показателем, потому что определяет вероятность выхода из строя системы. Определим ее как интеграл от р(
является очень важным показателем, потому что определяет вероятность выхода из строя системы. Определим ее как интеграл от р(![]() , подставив выражения для
, подставив выражения для ![]() из (3) в уравнение (4):
из (3) в уравнение (4):
![]() (7)
(7)
где L=![]() .
.
Введем обозначения в интеграле (7):
![]() = F. (8)
= F. (8)
Определим выражение для ![]() , возьмем производную d(
, возьмем производную d(![]() и подставим полученные выражения в формулу (7).
и подставим полученные выражения в формулу (7).
Взяв интеграл в пределах 0-Fmax, будем иметь
![]() , (9)
, (9)
где ![]() – неполная гамма-функция, значение которой определяются из таблиц [6].
– неполная гамма-функция, значение которой определяются из таблиц [6].
Тогда интегральная функция примет следующий вид:
![]() (10)
(10)
Если случайным процессом в системе является процесс усталости и его показателем – рост остаточной деформации и потеря устойчивости, вероятность выхода из строя системы будет определяться:
![]() (11)
(11)
а математическое ожидание и дисперсия определяются в соответствии с формулами (5), (6).
Предложенный метод исследуем на действующем мостовом металлургическом кране, используемом на кислородно-конвертерном цехе (ККЦ) ОАО ММК.
Для определения напряжений и деформаций необходимо рассчитать режим работы крана – характеристику, указывающую, можно ли эксплуатировать кран без ущерба его фактического технического состояния и надежности работы механизмов [8].
Режим работы крана – показатель, который учитывает его использование по грузоподъемности и времени, а также число циклов работы.
Количество циклов работы крана за срок его службы рассчитывается по формуле рабочих циклов:
CT = Cс * Пдн * Tк, (12)
где Сс – количество циклов работы крана в сутки;
Пдн – количество дней работы крана в году;
Tк – количество лет работы крана.
Режим нагружения крана характеризуется величиной коэффициента распределения нагрузок Kр.
В нашем случае кран грузоподъемностью 50 тонн работает в кислородно-конвертерном цехе металлургического предприятия 260 дней в году. Среднее число циклов, совершаемых краном в две смены, 600. Нормативный срок службы крана 15 лет. Общее количество циклов работы крана за весь срок его службы составит:
CT= Cс * Пдн * Tк = 600*260*15 = 2340000 циклов.
По таблице определяем класс использования как U7.
В массе перемещаемых краном грузов:
90 % составляют грузы массой до 40 тонн,
10 % – грузы массой до 10 тонн.
Определим коэффициент распределения нагружения:
Kp = 0,9*(40/40)^2+0,1*(10/40)^2 = 0,9 + 0,00625 = 0,90625.
Данному коэффициенту распределения нагрузок соответствует режим нагружения Q3 – тяжелый, Q4 – весьма тяжелый.
Общая группа классификации (режима работы) для класса использования U7 и режимов нагружения Q3, Q4 будет А8.
Расчет элементов машин на сопротивление усталости будем проводить по условию:
![]() , (13)
, (13)
где ![]() – длительный предел выносливости, определяемый с учетом асимметрии R, эффективного коэффициента концентрации напряжений k, размеров детали и ее термообработки;
– длительный предел выносливости, определяемый с учетом асимметрии R, эффективного коэффициента концентрации напряжений k, размеров детали и ее термообработки; ![]() – допускаемое напряжение;
– допускаемое напряжение; ![]() – коэффициент сопротивления усталости.
– коэффициент сопротивления усталости.
Определим характер появления деформаций и потери устойчивости при помощи метода преобразования вероятностей.
При полученных данных ![]() в относительных единицах, а
в относительных единицах, а ![]() МПа,
МПа, ![]() 0,786,
0,786, ![]() имеем:
имеем:![]() ,773.
,773.
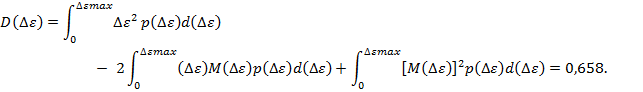
Определим параметр F из формулы (8) ![]() = 0,0093 – 1,3947.
= 0,0093 – 1,3947.
Используем функцию, возвращающую натуральный логарифм гамма-функции.
Тогда вероятность выхода из строя механической системы из-за роста остаточной деформации и увеличения прогибов выше допускаемых будет равна ![]() Возвращаясь к риск-анализу конструкции в целом и учитывая, что металлургический кран состоит из множества ответственных деталей, риск будет оцениваться как
Возвращаясь к риск-анализу конструкции в целом и учитывая, что металлургический кран состоит из множества ответственных деталей, риск будет оцениваться как ![]() и выше.
и выше.
Полученные данные согласуются с известными данными рисков металлургических предприятий и их различных элементов, что говорит о правомерности описанного подхода к прогнозированию и оценке надежности несущих конструкции мостовых кранов металлургических предприятий.
Полученная вероятность выхода из строя механической системы из-за роста остаточной деформации и увеличения прогибов достаточно высокая, это позволяет дополнить теорию конструкционного риск-анализа методом преобразования вероятностей и его дальнейшим развитием для предотвращения аварий и несчастных случаев и управления промышленной безопасностью сложных технических систем.
Рецензенты:
Черчинцев В.Д., д.т.н., профессор, заведующий кафедрой промышленной экологии безопасности жизнедеятельности, МГТУ им. Г. И. Носова, г. Магнитогорск.
Бигеев В.А., д.т.н., профессор, директор института машиностроения, металлургии и металлообработки МГТУ им. Г. И. Носова, г. Магнитогорск.



