Моделирование лесных пожаров является важной составляющей стратегии борьбы с ними. Современные подходы к моделированию лесных пожаров заключается в использовании математических постановок, основанных на физических законах. Химико-физические процессы являются одной из ключевых составляющих лесного пожара. Для их моделирования используется, как правило, закон Аррениуса, использование которого требует наличие информации о термокинетических постоянных этих процессов. Значения этих параметров оказывают существенное влияние на ход моделируемого пожара.
Для исследования процессов, происходящих при нагреве органических материалов, используется метод термогравиметрии, основанной на непрерывном измерении изменения массы исследуемого образца при температуре среды, изменяемой по заданному закону. Как известно, на результаты эксперимента оказывают существенное влияние такие факторы, как форма печи, материал контейнера для образца, размер и вес исследуемых частиц, форма, место расположения термопары, темп нагрева, проведение реакции в изотермических или неизотермических условиях. Эти факторы обуславливают часто плохую воспроизводимость термогравиметрических кривых.
Другой сложностью нахождения термокинетических констант является существенное отличие убыли массы в экспериментах от модельных расчётов, проводимых в предположении существования одной реакции, скорость которой определяется законом Аррениуса. Именно эти факторы обуславливают разброс в термокинетических константах. Немаловажным также является и существенные различия этих значений в зависимости от вида материала.
Так, в работах [1, 4, 6] авторами приводятся константы скорости и значения энергий активации для лесных горючих материалов (ЛГМ) Сибирских и Китайских лесов – хвои сосны, ели, кедра, а также веток и коры сосны. В работах [3, 5] авторы приводят константы скорости и значения энергий активации для различных образцов торфа.
Существуют множество методов определения кинетических констант реакций пиролиза конденсировнных систем (ЛГМ, полимеров) на основе экспериментальных термогравиметрических данных. Одним из известных является метод, основанный на логарифмировании уравнения изменения массы в форме Аррениуса, что позволяет привести его к шаблону линейной регрессии [2]. В результате этого минимизируемая ошибка определяется не абсолютной, а относительной погрешностью, что вполне приемлемо, если исследуется только одна реакция и погрешность в определении её скорости мала. Однако при нагреве органических материалов происходит множество реакций, в результате чего по мере уменьшения остаточной массы образца побочные реакции вносят существенную погрешность. В работе [3] на основе модифицированного закона Герца – Кнудсена авторы исследуют характеристики пиролиза на основе экспериментальных данных по потере массы от времени, полученных при различных значениях начальной температуры в изотермических условиях, и сопоставляют их с термогравиметрическими данными, полученными в неизотермических условиях. Для нахождения констант скорости двухстадийных последовательно-параллельных реакций окислительного пиролиза торфа и полимеров при тлеющем их горении в работах [5, 7] применялся генетический алгоритм, представляющий собой эвристический метод поиска, имитирующий принципы биологической адаптации на основе дарвинистский теории естественного отбора. В работе [5] определено 16 параметров. Определение кинетических параметров было выполнено с помощью минимизации параметра Φ, содержащего массу и скорость ее изменения (данные ТГ и ДТГ)
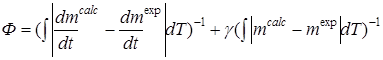 , (1)
, (1)
где γ = 0,5. В работах [4, 6] кинетический анализ пиролиза лесных горючих материалов в окислительной среде был проведен с использованием механизма для многокомпонентных веществ. Процесс потери массы лесных горючих материалов моделируется четырьмя параллельными реакциями, в соответствии с разложением трех основных компонентов биомассы (гемицеллюлоза, целлюлоза и лигнин) и окисления углеродного остатка. Определение кинетических параметров для каждой реакции было выполнено с помощью минимизации SDTG , коэффициента экспериментальных данных
![]() (2)
(2)
где m, T – масса, температура, индексы “exp” and “simu” означают экспериментальное и рассчитанное значения, ![]() число экспериментальных кривых и
число экспериментальных кривых и ![]() число точек для каждого эксперимента. Минимизация SDTG выполнена нелинейным алгоритмом подгонки с помощью программы Matlab. Для оценки соответствия экспериментальных и моделируемых данных используется параметр Dev
число точек для каждого эксперимента. Минимизация SDTG выполнена нелинейным алгоритмом подгонки с помощью программы Matlab. Для оценки соответствия экспериментальных и моделируемых данных используется параметр Dev
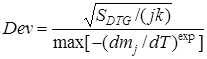 (3)
(3)
Величина этого параметра была равна 2 %.
В данной работе представлен анализ экспериментальных термогравиметрических данных пиролиза иголок сосны, полученных в ИХКГ СО РАН, с помощью алгоритма, разработанного в НГТУ им. Р.Е. Алексеева.
Предполагается, что существуют две последовательные реакции, причём продукт первой является реагентом для второй.
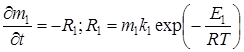 , (4)
, (4)
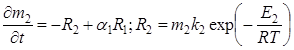 , (5)
, (5)
![]() . (6)
. (6)
При анализе экспериментальных данных предполагается, что массе экспериментального образца соответствует сумма масс каждой из рассматриваемых в модели компонент конденсированной фазы.
![]() (7)
(7)
В качестве начальных условий используются соотношения.
![]() (8)
(8)
В уравнениях (4–8) приняты обозначения: i – порядковый номер реагирующего вещества; mi(t) – масса i-й компоненты сухого органического вещества в процессе реакции на момент t; kj, Ej – предэкспонента и энергия активации j-й стадии реакции пиролиза, подбираемые с помощью решения обратной задачи; αj – отношение массы продукта j-й стадии реакции к массе исходного вещества на данной стадии. Температура T(t) изменяется по заданному закону. Во всех рассмотренных в данной работе экспериментах эта зависимость линейная.
Для решения обратной задачи в данной работе авторами предлагается алгоритм, вычисляющий термокинетические параметры стадий на основе экспериментальных данных ТГА (термогравианалитической кривой), полученных в результате нагрева образца с заданной скоростью (10 К/с).
На первом этапе алгоритма происходит очистка данных, а именно – группы последовательных строк с одинаковой массой образца заменяются одной строкой. Температура и время устанавливается равными среднему арифметическому между первой и последней строками данной группы. Такой приём позволяет существенно уменьшить колебания производной.
Далее алгоритм приводит очищенные от повторов экспериментальные данные к заданной равномерной сетке температур с использованием сплайн-интерполяции.
На следующем этапе вычисляется скорость относительной потери массы с помощью соотношения:
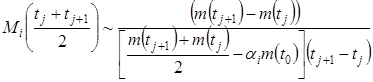 , (9)
, (9)
где Mi – скорость относительной убыли массы i-го компонента, ti,– время на соответствующем j-м шаге сетки (tj+1), ![]() t0 – начальный момент времени в анализе данной стадии, αi – величина условно нереагирующего остатка после i-й стадии. Соотношение (9) учитывает также условно нереагирующий остаток.
t0 – начальный момент времени в анализе данной стадии, αi – величина условно нереагирующего остатка после i-й стадии. Соотношение (9) учитывает также условно нереагирующий остаток.
Перед запуском итерационного процесса определяются достаточно грубые верхняя и нижняя оценки энергии активации Emin и Emax. На каждой итерации происходит следующий процесс:
1) Вычисляется значение ![]() , являющееся на данном этапе предполагаемой энергией активации.
, являющееся на данном этапе предполагаемой энергией активации.
2) Выполняется оценка скорости расхода вещества на основе предполагаемого значения энергии активации
![]() , (10)
, (10)
3) Вычисляется предэкспонента, при которой убыль массы по эксперименту будет совпадать с модельным расчётом при энергии активации Etest.
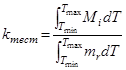 (11)
(11)
где jmin – индекс, соответствующий минимальной температуре анализируемого отрезка, а jmax – максимальной.
4) Вычисляется расчётная относительная скорость потери массы
![]() (12)
(12)
5) Оценивается квадрат ошибки (с учётом знака) отклонения экспериментальных данных от расчётных значений по соотношению (13). Положительный знак указывает на то, что расчётная величина скорости относительной потери массы больше экспериментальной.
![]() (13)
(13)
6) Определяется знак интеграла
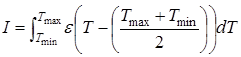 (14)
(14)
7) Если интеграл (14) положителен, значит, расчётная скорость относительной потери массы принимает большие значения, чем экспериментальная, при более низкой температуре, но меньшие – при более высокой. Это в свою очередь означает, что рост скорости реакции с температурой недооценён, и, следовательно, предполагаемая энергия активации является нижней оценкой Emin. В противном случае она является верхней оценкой Emax.
8) Если заданная точность не достигнута, то выполняется следующая итерация, иначе полученные значения Etest и Ktest считаются окончательным решением.
На основе описанного алгоритма был разработан программный комплекс. С его помощью были выполнены расчёты термокинетических постоянных по данным ТГА при нагреве хвоинки в окислительной среде (20 % O2). На рис. 1 показано сопоставление экспериментальных данных и решения прямой задачи при найденных константах для данного эксперимента.
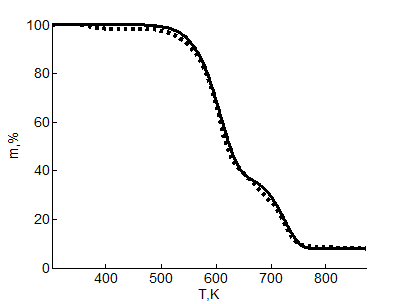
Рис. 1. Сопоставление экспериментальных (пунктирная линия) и расчётных (сплошная линия) данных для нагрева образца в окислительной среде
При нагреве образца в окислительной среде (20 % O2) было выявлено две стадии: первая стадия доминирует при температуре от 400 до 600К, а вторая от 660 до 730К. При этом термокинетические параметры первой стадии: k1=1.082·106 сек-1, Е1=96696 Дж/моль, второй стадии – k2=9.489·107 сек-1; Е=140654 Дж/моль. Условно нереагирующие остатки α1=0.37, α2=0.216. При температурах ниже выбранного диапазона могут происходить другие реакции, которые не влияют на результат, что видно из рис. 1.
Результат решения обратной задачи также существенно зависит от выбора отрезка температур в связи с тем, что реальные химические процессы, имеющие место при проведённом эксперименте, могут быть представлены в виде одной или двух стадий лишь приблизительно. Следует отметить, что нереагирующий остаток в реакции пиролиза существенно превышает долю остаточной массы при нагреве в инертной среде, что можно объяснить возможностью более глубокого пиролиза в отсутствии кислорода.
Работа выполнена при финансовой поддержке 13-03-91164-ГФЕН_а «Экспериментальное исследование кинетики и механизма термического разложения лесных горючих материалов и процессов распространения пламени по их слою».
Рецензенты:
Петрухин Н.С., д.ф.-м.н., ординарный профессор Национального исследовательского университета «Высшая школа экономики», г. Нижний Новгород.
Карпухин В.Б., д.ф.-м.н., профессор кафедры «Высшая и прикладная математика» Российской открытой академии транспорта Московского государственного университета путей сообщения, г. Москва.



