Скрытая марковская модель (СММ) – модель, имитирующая работу реального процесса, позволяющая определить его неизвестные параметры на основе наблюдаемых. Теория СММ формирует основу индустриального стандарта для приложений осуществляющих распознавание речи [1].
Каждая СММ λ=(A,B,π) представляет собой набор N состояний S={S1,S2,…,SN} между которыми возможны переходы. В момент времени t система может находиться только в одном из состояний. При переходе из одного состояния в другое генерируется наблюдаемый символ, который соответствует физическому сигналу с выхода моделируемой системы. Набор символов для каждого состояния – V={v1,v2,…,vM}, количество символов – M. Символ в состоянии qt=Sj, в момент времени t генерируется с вероятностью bjk=P(vk|qi=Sj). Набор всех таких вероятностей составляет матрицу B={bjk}.
Матрица A=||aij|| определяет вероятность перехода из одного состояния в другое: aij=P(qi+1=Sj|qi=Si), 1≤i, j≤N. Вероятность нахождения системы в начальный момент времени описывается как π={πi}, где πi=P(q1=Si) [1].
В общем случае каждое состояние Sj модели λ может быть достигнуто за один шаг из любого другого состояния Si. Такая модель называется эргодической. Каждая переходная вероятность aij эргодической СММ строго положительна. На практике моделируемый сигнал может не отвечать данному требованию, в результате за годы использования СММ в системах распознавания, было разработано множество топологий и конфигураций. Выбор структуры СММ во многом определяется областью применения и предшевствующим опытом разработчика. Применительно к задаче установления личности наиболее очевидным решением является выбор структуры СММ, отражающей физиологические особенности строения лица человека.
Глядя на изображение лица, можно выделить ряд верикальных областей: волосы, лоб, брови, глаза, нос, рот и подбородок, при этом области следуют строго друг за другом, пропуск или изменение порядка следования областей невозможен, если человек не обладает ярко выраженными физическими отклонениями. В роли начальной области всегда выступают «волосы», в роли конечной – «подбородок». На основании сказанного можно заключить, что наиболее подходящей для описания лица является лево-правая модель СММ (модель Бакиса) [2].
Последовательность состояний модели Бакиса обладает тем свойством, что с увеличением времени, индекс состояния не может уменьшаться, иными словами, состояния переходят из одного в другое только слева направо. Поскольку в лево-правой модели не разрешены переходы в состояния, индекс которых меньше индекса текущего сотояния, основное свойство всех лево-правых СММ выражается через значения переходных вероятностей следующим образом:
![]()
Кроме того, поскольку последовательность состояний должна начинаться в сотсоянии 1, а заканчиваться в состоянии N, начальное распределение вероятностей состояний обладает свойством:
![]()
Для того чтобы избежать значительных скачков в индексах состояний при использовании лево-правых моделей на переходные вероятности, как правило, налагаются дополнительные ограничения:
![]()
Переходные вероятности для последнего состояния лево-правой модели определяются следующим образом:
![]()
![]()
Таким образом, лево-правая модель хорошо согласуется с особенностями изображения человеческого лица, получемого с систем фото- и видеофиксации. Поскольку обработка изображений в системах распознавания производится слева-направо, сверху-вниз, гарантируется переход только между соседними состояниями.
На практике зачастую производят объединение области бровей с областью глаз, а области рта – с областью подбородка, это дает возможноть получить начальные значения СММ путем разбиения изображения на пять равных частей [3, 4]. Недостатком лево-правой модели являтся то, что она не учитывает пространственных особенностей изображения, представляя его в виде линейной цепочки событий.
Псевдодвухмерные СММ имеют большой потенциал в области обработки двумерных массивов данных. Псевдодвухмерная СММ является обобщением СММ, где каждое состояние само по себе является одномерной СММ. Таким образом, псевдодвухмерная СММ состоит из набора супер состояний, каждое из которых содержит набор вложенных состояний. Такая СММ характеризуется следующим набором параметров:
- Количество суперсостояний N0. Множество супер состояний обозначается как ![]() .
.
- Начальное распределение вероятностей супер состояния П0 = {π0,i}, где π0,i вероятность нахождения в супер состоянии i в начальный момент времени.
- Матрица распределения вероятности перехода между супер состояниями, A0 = {a0,ij}, где a0,ij вероятность перехода из супер состояния i в супер состояние j.
Матрица распределения вероятности появления состояния, ![]() , где
, где ![]() – вектор наблюдений для строки t0 и столбца t1. Функция распределения вероятности, может быть представлена как:
– вектор наблюдений для строки t0 и столбца t1. Функция распределения вероятности, может быть представлена как:
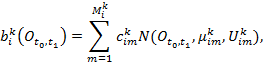
где ![]() функция нормального распределения.
функция нормального распределения.
Параметрами вложенной СММ Λ являются:
- Количество вложенных состояний к k-ом супер состоянии, ![]() и множество вложенных состояний,
и множество вложенных состояний, ![]() .
.
- Начальное распределение вероятностей состояний, ![]() , где
, где ![]() вероятность нахождения в состоянии i супер состояния k в начальный момент времени.
вероятность нахождения в состоянии i супер состояния k в начальный момент времени.
- Матрица вероятности переходов между состояниями, ![]() , описывающая вероятность перехода из состояния k в состояние j.
, описывающая вероятность перехода из состояния k в состояние j.
На рисунке 1 представлена описанная структура СММ, каждое состояние в которой само по себе является лево-правой моделью СММ [5].
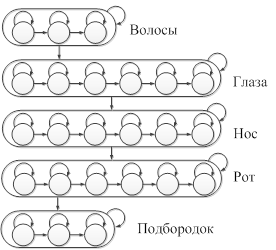
Рисунок 1 – Структура псевдодвухмерной СММ с пятью супер состояниями
Вероятность наблюдения одного из состояний вложенной СММ описывается с помощью распределения Гаусса:
![]()
Псевдодвухмерная модель СММ имеет более сложную структуру по сравнению с лево-правой моделью, однако она в большей степени отражает характерные особенности изображения лица, учитывая не только его вертикальную, но и горизонтальную структуру.
В таблице 1 представлены результаты распознавания, полученные с использованием лево-правой и псевдодвухмерной структур, а также производительность каждого варианта системы распознавания.
Таблица 1 – Обобщенные результаты проведенного эксперимента
|
Тестовая база |
Процент правильно распознанных изображений |
Количество изображений, обработанных за 1 секунду |
||
|
Лево-правая модель |
Псевдо-двухмерная модель |
Лево-правая модель |
Псевдо-двухмерная модель |
|
|
The ORL Database of Faces |
96,5% |
99,5% |
3,92 |
3,46 |
|
Cohn-Kanade AU-Coded Facial Expression Database |
91,75% |
96,9 |
3,17 |
2,69 |
|
MIT-CBCL Face Recognition Database |
93,8% |
95,65% |
3,78 |
3,33 |
|
Face Recognition Data, University of Essex, UK |
89,76% |
93,75% |
3,63 |
3,15 |
Полученные данные позволяют сделать вывод о том, что использование псевдодвухмерной системы увеличивает количество правильно распознанных объектов в среднем на 4%. Это обусловлено тем, что такая модель позволяет учитывать локальные деформации и взаимное расположение участков изображения. Отрицательной стороной является значительный рост осуществляемых вычислений, что приводит к снижению производительности на 12,9%. Для систем, работающих в режиме реального времени, такой показатель может быть критичен.
Таким образом, применение псевдодвухменой модели оправданно в том случае, если необходимо обеспечить повышенную точность распознавания, притом что время распознавания не является критичным. К таким задачам можно отнести аутентификацию пользователей персональных компьютеров и смартфонов, контроль доступа персонала к закрытым помещениям и т.д.
Рецензенты:
Бабич М.Ю., д.т.н, главный специалист ОАО «НПП «Рубин», г. Пенза.
Светлов А.В., д.т.н, профессор, заведующий кафедрой «Радиотехника и радиоэлектронные системы» Пензенского государственного технологического университета, г. Пенза.



