В контексте происходящих процессов реформирования всей системы высшего образования в России одной из главных является проблема повышения качества образования и оценивания качества обучения в вузах [5, 7] и, в частности, анализ результатов входного контроля в вузе в основном по математике [1, 2, 4, 10], реже по физике [9] и химии [6]. В связи с этим представляет интерес сравнительный статистический анализ результатов входного контроля по математике, физике и химии на базе данных результатов входного тестирования (ВТ), проведенного в Томском политехническом университете (ТПУ) по математике (МАТЕМ), физике (ФИЗИКА) и химии (ХИМИЯ) наряду с вступительными испытаниями на основе результатов ЕГЭ в начале первого семестра 2013-2014 учебного года. Задание ВТ для студентов-очников по математике и химии содержали 20, а по физике – 16 задач средней сложности (типа группы «В» в билетах ЕГЭ).
Все числовые результаты ВТ приведены к единой 5-балльной шкале (делением результата на соответствующий максимальный результат и умножением на пять). Созданная таким образом в MS Excel база данных использовалась далее в пакете Statistica [3] для статистического анализа данных.
Распределения (гистограммы) по всем предметам приведены на рис. 1.
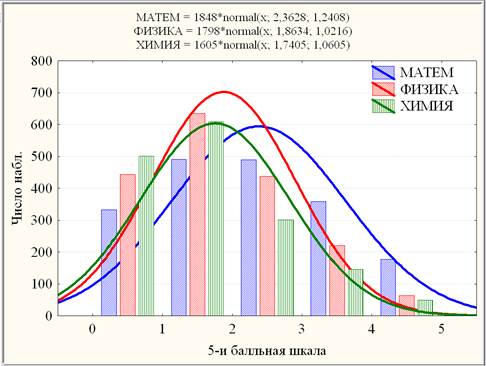
Рис.1. Составная гистограмма результатов ВТ ТПУ 2013г. по предметам с соответствующими кривыми нормального распределения
Согласно χ2-критерию Пирсона, распределения (гистограммы) по всем предметам высоко значимо (на уровне значимости р<0,0005) отличаются от соответствующих теоретических нормальных распределений (кривые) по МАТЕМ, ФИЗИКА и ХИМИЯ с параметрами (N – объем выборки, m – выборочное среднее, σ – выборочное стандартное отклонение), указанными на рис.1 в формате ПРЕДМЕТ = N*normal(x, m, σ).
Дисперсионный анализ (параметрический F-критерий и ранговый критерий Краскела-Уоллиса) оценивает различие результатов ВТ ТПУ по предметам как высоко значимое (р < 0,0005) за счет высоко значимого отличия результатов ВТ ТПУ по МАТЕМ от ФИЗИКА и ХИМИЯ при сильно значимом (0,0005 < p=0,001 < 0,005) различии результатов ФИЗИКА и ХИМИЯ.
Корреляционную зависимость МАТЕМ, ФИЗИКА и ХИМИЯ характеризуют коэффициенты парной корреляции (параметрический Пирсона r и ранговый Спирмена R). Матрицы коэффициентов парных корреляций переменных приведены в табл. 1 (Пирсона r – в право-верхнем треугольнике над диагональю и Спирмена R – в лево-нижнем треугольнике под диагональю). Все корреляции можно считать высоко значимо ( р < 0,0005) отличающуюся от ноля, тем не менее далекими от единицы. При этом коэффициенты парных корреляций Пирсона r отличаются от соответствующих ранговых корреляций Спирмена R незначимо. Согласно табл. 1, наиболее сильной корреляционной зависимостью связаны МАТЕМ и ФИЗИКА. В рамках кластерного анализа проведена иерархическая классификация предметов по совокупности институтов, отражающая корреляционную зависимость предметов (в качестве меры близости выбрано корреляционное расстояния 1 – r) и построена дендрограмма предметов (рис. 2).
Таблица 1. Матрица коэффициентов парных корреляций: Пирсона r – в право-верхнем треугольнике и Спирмена R – в лево-нижнем треугольнике под диагональю
|
|
М |
Ф |
Х |
|
|
МАТЕМ |
1,000 |
0,595 |
0,494 |
r |
|
ФИЗИКА |
0,600 |
1,000 |
0,475 |
|
|
ХИМИЯ |
0,488 |
0,457 |
1,000 |
|
|
|
R |
|
||
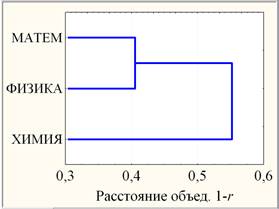
Рис. 2. Дендрограмма предметов
Во ВТ по предметам участвовали студенты-очники первого курса ТПУ набора 2013 г. 6-и институтов [8]: кибернетики (ИК), природных ресурсов (ИПР), энергетического (ЭНИН), физики высоких технологий (ИФВТ), физико-технического (ФТИ) и неразрушающего контроля (ИНК).
Таким образом, в данной работе рассматривается 2-х факторная дисперсионная модель ВТ (3-х уровневый фактор «ПРЕДМЕТ» и 6-и уровневый фактор «ИНСТИТУТ»).
Графики предметных средних баллов результатов ВТ по институтам с указанием 95 % доверительного интервала приведены на рис. 3.
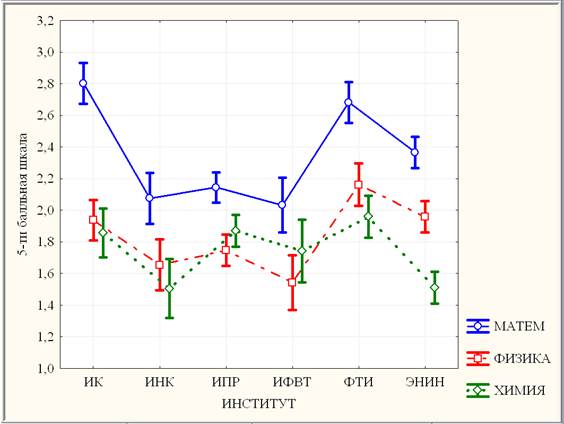
Рис. 3. Линейные графики предметных средних результатов ВТ 2013г. по институтам
Применение параметрического F-критерия дисперсионного анализа приводит к выводу о высоко значимой неоднородности результатов ВТ по совокупности институтов для любого предмета.
Параметрические (среднее, стандартная ошибка, ±95% границы доверительных интервалов, объем n) числовые характеристики выборок результатов ВТ студентов 6-и институтов ТПУ по 3-м предметам приведены в табл. 2.
Таблица 2. Характеристики выборок результатов ВТ по предметам и институтам
|
ПРЕДМЕТ |
ИНСТИТУТ |
Среднее |
Стд. ош. |
-95% |
+95% |
n |
|
МАТЕМ |
ИК |
2,803 |
0,066 |
2,674 |
2,932 |
278 |
|
МАТЕМ |
ИНК |
2,075 |
0,083 |
1,913 |
2,237 |
176 |
|
МАТЕМ |
ИПР |
2,145 |
0,049 |
2,049 |
2,240 |
505 |
|
МАТЕМ |
ИФВТ |
2,032 |
0,088 |
1,859 |
2,205 |
154 |
|
МАТЕМ |
ФТИ |
2,682 |
0,066 |
2,552 |
2,811 |
275 |
|
МАТЕМ |
ЭНИН |
2,366 |
0,051 |
2,266 |
2,466 |
460 |
|
ФИЗИКА |
ИК |
1,938 |
0,066 |
1,809 |
2,067 |
278 |
|
ФИЗИКА |
ИНК |
1,655 |
0,083 |
1,493 |
1,817 |
176 |
|
ФИЗИКА |
ИПР |
1,747 |
0,050 |
1,649 |
1,846 |
475 |
|
ФИЗИКА |
ИФВТ |
1,544 |
0,088 |
1,371 |
1,717 |
154 |
|
ФИЗИКА |
ФТИ |
2,162 |
0,069 |
2,027 |
2,296 |
255 |
|
ФИЗИКА |
ЭНИН |
1,959 |
0,051 |
1,859 |
2,059 |
460 |
|
ХИМИЯ |
ИК |
1,857 |
0,079 |
1,702 |
2,013 |
191 |
|
ХИМИЯ |
ИНК |
1,506 |
0,095 |
1,320 |
1,691 |
134 |
|
ХИМИЯ |
ИПР |
1,871 |
0,052 |
1,769 |
1,972 |
446 |
|
ХИМИЯ |
ИФВТ |
1,744 |
0,101 |
1,545 |
1,942 |
117 |
|
ХИМИЯ |
ФТИ |
1,959 |
0,068 |
1,825 |
2,093 |
257 |
|
ХИМИЯ |
ЭНИН |
1,511 |
0,051 |
1,411 |
1,611 |
460 |
Диаграмма рассеяния институтских средних ВТ по предметам изображена на рис. 4.
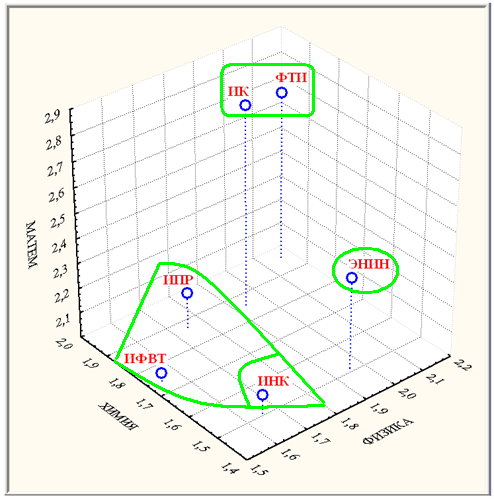
Рис. 4. Диаграмма рассеяния институтских средних ВТ по предметам
Согласно апостериорному критерию наименьшей значимой разности, эквивалентному t-критерию для числа независимых выборок больше двух, выделены для каждого предмета однородные (различающиеся незначимо, то есть на уровне значимости р > 0,10) группы институтов, расположенные в порядке убывания средних:
- МАТЕМ: {ИК, ФТИ}, {ЭНИН}, {ИПР, ИНК, ИФВТ}. При этом ЭНИН сильно значимо (0,0005 < p=0,002 < 0,005) отличается от ИПР и высоко значимо (p < 0,0005) отличается от ФТИ.
- ФИЗИКА: {ФТИ}, {ЭНИН, ИК}, {ИПР, ИНК}, {ИНК, ИФВТ}. При этом ИПР статистически значимо (0,005 < p=0,045 < 0,05) отличается от ИФВТ.
- ХИМИЯ: { ФТИ, ИПР, ИК, ИФВТ}, {ЭНИН, ИНК}. При этом ФТИ слабо значимо ((0,05 < p=0,08 < 0,10)) отличается от ИФВТ, но высоко значимо (p < 0,0005) отличается от ЭНИН, который статистически значимо (0,005 < p=0,04 < 0,05) отличается от ИФВТ.
В данной работе на базе данных выборки ВТ проведен кластерный анализ институтов по совокупности предметов. В рамках кластерного анализа методом K-средних, проводящим классификацию институтов по заданному количеству кластеров, рассмотрена 3-х (толстая красная горизонтальная прямая на рис. 5 слева) кластерная модель: К1 = {ИК, ФТИ} по совокупности высоких результатов по всем предметам, промежуточный моно кластер К21 = {ЭНИН} и К22 = {ИФВТ, ИНК, ИПР} по совокупности низких результатов по математике и физике. Заметим, что деление 6-ти институтов на 3 кластера является устойчивым как по отношению к выбору мер близости (евклидового, манхеттенского или чебышевского расстояния), так и правилам объединения кластеров (метода полной связи, метода Уорда (Варда) и т.д.), реализованным в пакете Statistica. По рассчитанным кластерным средним для наглядного оценивания значимости различий построены их линейные графики на рис. 5 справа.
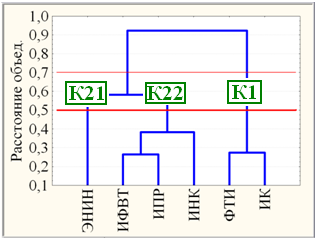
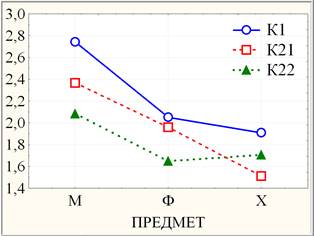
Рис. 5. Дендрограмма институтов (слева) и графики кластерных средних институтов по предметам в случае 3-х кластерной модели (справа)
При этом, согласно параметрическому F-критерию (табл. 3), 6 институтов разделены на 3 кластера по математике сильно значимо (0,0005 < p» 0,004 < 0,005); по физике – слабо значимо (0,05 < p» 0,075 < 0,10); по химии – незначимо (0,10 < p) вследствие широкого размаха средних по химии для институтов кластера К22 = {ИФВТ, ИНК, ИПР}. Как следует из рис. 5 слева, на уровне деление 6-ти институтов на 4 кластера из кластера К22 выделяется в моно кластер ИНК, наиболее отличающийся по химии от ИФВТ и ИПР (рис. 4).
Таблица 3. Результаты дисперсионного анализа качества 3-х кластерной модели институтов 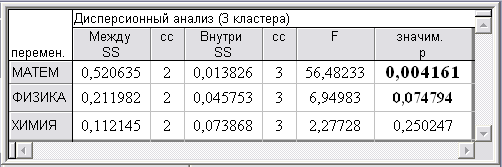
Проведенный статистический анализ результатов входного тестирования по предметам позволяет выяснить реальную подготовленность первокурсников к изучению дисциплины и использовать их при формировании групп для дополнительных занятий.
Выводы
1. На основании критерия хи-квадрат выявлено высоко значимое отличие распределений результатов ВТ предметов от нормального закона.
2. Корреляция между результатами ВТ предметов высоко значимо отличается от ноля, хотя далека от единицы. При этом коэффициенты парных корреляций Пирсона r отличаются от соответствующих ранговых корреляций Спирмена R не значимо.
3. Дисперсионный анализ (параметрический F-критерий и ранговый критерий Краскела-Уоллиса) оценивает различие результатов ВТ ТПУ по предметам как высоко значимое (р < 0,0005) за счет высоко значимого отличия результатов ВТ ТПУ по математике от физики и химии при сильно значимом (0,0005 < p=0,001 < 0,005) различии результатов физики и химии.
4. Различие результатов ВТ ТПУ для любого предмета оценивается на основании параметрического F-критерия дисперсионного анализа как высоко значимое (р < 0,0005) по совокупности институтов. Для каждого предмета выделены однородные (различающиеся незначимо) группы институтов.
5. В рамках кластерного анализа методом K-средних 6 институтов разделены на 3 кластера, один из которых содержит два института, однородных по совокупности высоких результатов по всем предметам, промежуточный по результатам моно кластер и кластер из трех институтов, однородных по совокупности низких результатов по математике и физике.
Работа выполнена в рамках государственного задания «Наука» № 1.604.2011 и поддержана ФЦП «Научные и научно-педагогические кадры инновационной России» по контрактам П691.
Рецензенты:
Трифонов А.Ю., д.ф.-м.н., профессор кафедры высшей математики и математической физики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.
Арефьев К.П., д.ф.-м.н., профессор кафедры высшей математики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.



