Введение

Применение смешанного метода конечных элементов (МКЭ) совместно с ортогональными финитными функциями (ОФФ) для решения краевых задач трехмерной теории упругости позволяет получать результаты, обладающие уравновешенной точностью и гладкостью [1]. Однако существенным недостатком смешанного метода конечных элементов является высокая размерность получаемых сеточных систем уравнений. В данной статье предлагается новый алгоритм решения задач трехмерной теории упругости в форме смешанного метода конечных элементов с использованием ОФФ, что позволило преодолеть недостатки этого метода.

Цель исследования

Разработка алгоритма смешанного метода конечных элементов с использованием ортогональных финитных функций для решения технических задач трехмерной теории упругости.

Методы и результаты исследований

В рамках работы были использованы методы конечно-элементного моделирования, численные методы решения систем линейных уравнений, объектно-ориентированного и структурного программирования, вариационного исчисления и механики сплошных сред.

Система уравнений трехмерной задачи теории упругости состоит из трех уравнений равновесия и шести соотношений обобщенного закона Гука с учетом термоупругости:

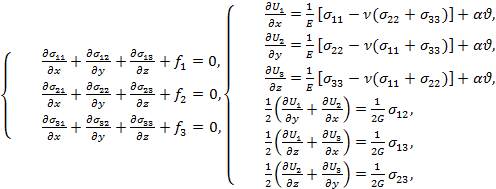(1)

где — компоненты симметричного тензора напряжений , — компоненты вектора перемещений , — компоненты вектора объемных сил, — коэффициент линейного теплового расширения, — заданное поле температуры, — модуль Юнга, — коэффициент Пуассона, — модуль сдвига.

Функционал Рейсснера [4] для данной задачи запишется следующим образом:

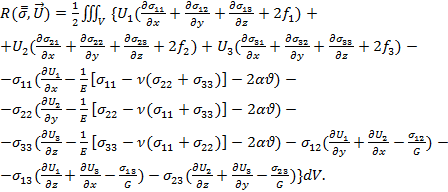(2)

Отыскиваемые величины в матричной форме для каждого конечного элемента обозначаются так:

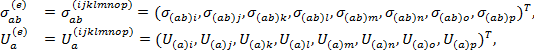(3)

где — номер элемента, — номера узлов, соответствующих данному элементу с индексом .

Локальная матрица аппроксимирующих функций записывается в виде:

(4)

Функционал (2) после подстановки в него в качестве отыскиваемых величин их произведений с аппроксимирующими функциями в матричной форме (например, ) принимает вид:

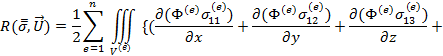
  (5)

Введем обозначения матричных коэффициентов, содержащих частные производные по , и :

(6)

С помощью преобразований:

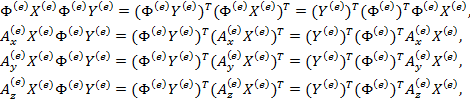(7)

которые позволяют вынести из под знака интеграла величины , независящие от , или и представляющие собой одну из величин из (3), получим функционал, представляющий собой дискретную модель трехмерного упругого тела:

где

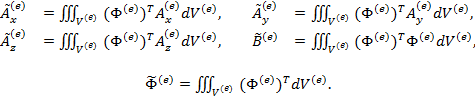(9)

Форма применяемого конечного элемента показана на рис. 1.

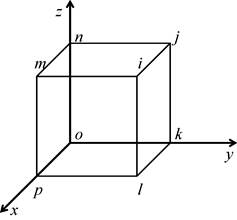
Рисунок 1– Форма трехмерного конечного элемента

Трехмерные аппроксимирующие функции матрицы (4) определяются тензорными произведениями одномерных функций Куранта [5] или ортогональных финитных функций [1, 2, 3]:

(10)

где является правой частью функций, а — их левой частью относительно центра конечного носителя функции. Таким образом, при подстановке функций Куранта, функция имеет вид:

(11)

Аналогичным образом определяются функции для всех остальных узлов:

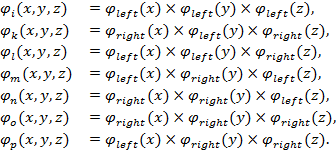(12)

Интегрирование выражений (9) приводит к получению основных матриц аппроксимирующих функций, которые для функций Куранта имеют вид:

где — площади граней конечного элемента , параллельных плоскостям соответственно; — объем конечного элемента . Для функций Куранта , для ортогональных финитных функций . При использовании ортогональных финитных функций все элементы представленных матриц, отличные от или , равны нулю, что приводит к четырехкратному уменьшению количества коэффициентов для каждой из матриц с производными и к восьмикратному уменьшению количества коэффициентов матрицы , для которой ненулевыми останутся только элементы главной диагонали.

Продифференцируем функционал для элемента по переменным -го узла и , приравнивая результат к нулю:

Выражения в круглых скобках образуют локальную подсистему для узла конечного элемента , где , , . Задание граничных условий приводит к возникновению дополнительных слагаемых в соответствующих уравнениях локальных подсистем. В частности, если узел закреплен по оси (не может перемещаться вдоль данной оси), то во всех уравнениях, содержащих коэффициенты с производными, при величинах , и возникают дополнительные слагаемые , , .

Построение глобальной матрицы жесткости осуществляется непосредственной подстановкой коэффициентов локальных подматриц для каждого из узлов конечного элемента.

Верификация алгоритма была проведена при решении технологических задач формообразования, в числе которых моделирование формообразования профиля специальной формы из перфорированной ленты. Целью моделирования являлась разработка схемы формообразования и получение технологических параметров формообразующего инструмента. В качестве материала при моделировании профиля была выбрана сталь 08кп. Особенностью схемы формообразования являлось исключение контакта формообразующего инструмента с перфорированными областями профиля (рис. 2).

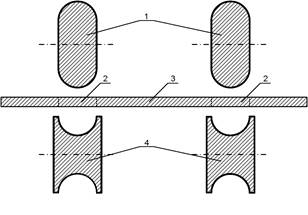
Рисунок 2 – Моделируемая схема формообразования профиля корытообразного типа специальной формы: 1 — верхние ролики; 2 — угловые зоны профиля; 3 — перфорированная лента (заготовка); 4 — нижние ролики

Характерной особенностью формообразования в роликовых калибрах является постоянный контакт инструмента (роликов) с поверхностями заготовки. В данном случае ставилась задача исключения контакта боковой поверхности с перфорированной частью заготовки. При этом область пластических деформаций (угловая зона) должна быть локализована только в специально предназначенной неперфорированной области заготовки (рис. 3).

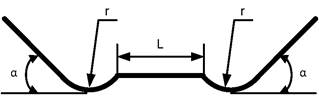
Рисунок 3 – Сечение искомого профиля: — требуемый радиус скругления; — требуемый угол подгибки полки профиля; — протяженность плоского участка дна профиля

Постпроцессорная обработка (рис. 4) позволила получить требуемые технологические параметры для каждого перехода: угол подгибки полок профиля, угол изгиба дна профиля, величину перемещения инструмента и радиус скругления угловых зон.

а) 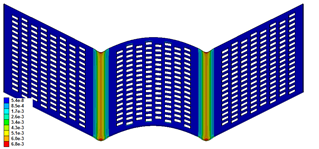б)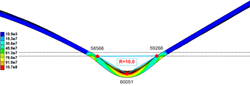

Рисунок 4 – Величина деформации элементов профиля (а) и угловой зоны (б) на третьем этапе формообразования

Технологические параметры формообразования профиля, полученные в результате конечно-элементного моделирования, представлены в таблице 1.

Таблица 1

Результаты конечно-элементного моделирования

Выводы

Предложенный алгоритм был программно реализован в авторском комплексе конечно-элементного анализа в смешанной форме ViSolver (свидетельство о государственной регистрации № 2012617956 от 3 сентября 2013 г.). Анализ результатов был произведен в программной среде ViPost, которая является составной частью комплекса ViSolver.

В результате проделанной работы была получена схема формообразования и основные технологические параметры процесса. Проведен расчет суммарной величины подгибки полок профиля.

Рецензенты:

Антонов И.С., д.т.н., зав. кафедрой проектирования и сервиса автомобилей, ФГБОУ ВПО «Ульяновский государственный университет», г. Ульяновск.

Светухин В.В., д.ф.-м.н., профессор, директор научно-исследовательского технологического института УлГУ, ФГБОУ ВПО «Ульяновский государственный университет», г. Ульяновск.