Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

С ростом конкуренции во многих областях экономики, требующих вложения больших объемов инвестиций и реализации крупных проектов, будь то строительство недвижимости, инфраструктурное развитие, автомобилестроение или другие, ужесточаются требования к точности принимаемых решений и обоснованности выбора конкретного проекта из множества альтернативных вариантов.

Совершенно очевидно, что разработка новых направлений в определении эффективности инвестиционных проектов и доработка уже существующих методов, базирующихся как на оценках денежной природы, так и предполагающих комплексный подход к оценке последствий реализации проектов, дает конкурентное преимущество компании, работающей над модернизацией методической базы.

Характерной особенностью развития российской экономики на современном этапе является принятие решений при высокой степени неопределенности исходной информации об условиях реализации проектов. Распространенным способом поиска решения является проведение дискуссии. Проблема такого способа принятия решения состоит в больших затратах времени, а также он может оказаться субъективным, поскольку проводится в условиях неточности и сильной информационной неопределенности [6].

Альтернативой такому подходу является применение метода анализа иерархий (МАИ, в англо-американской литературе AHP – analitical hierarchy process [4]), являющегося совокупностью логических и математико-статистических процедур и методов, направленных на обработку полученных от группы экспертов знаний. Метод анализа иерархий был предложен около 30 лет тому назад Т. Саати [4] и получил достаточно широкое применение в сфере принятия решений в условиях неопределенности. Его основные преимущества состоят в возможности интеграции в процессе принятия решения целого набора различных количественных и качественных факторов и определенного упрощения поиска решений путем декомпозиции сложной проблемы во взаимосвязанную последовательность более простых задач.

Математическая сторона МАИ базируется на теории обратносимметрических матриц и девятибалльной шкале сравнений альтернатив.

Для упрощения построения моделей, обеспечения быстроты расчетов, получения возможности графического отображения результатов метод анализа иерархий был реализован сразу в нескольких экспертно-аналитических системах для персональных компьютеров, среди которых хотелось бы выделить лишь две.

Первой является экспертно-аналитическая система Expert Decide, разработанная в 2000-2001 гг. специалистами Орловского государственного технического университета (ОГТУ) и Орловской региональной академии государственной службы (ОРАГС) [1]. Она обладает доступным и интуитивно понятным пользовательским интерфейсом и широкими возможностями графического вывода.

Алгоритмы МАИ/AHP были также положены в основу более поздней разработки – экспертно-аналитической системы Expert Solution 1.0 [3], специально предназначенной для сравнительного анализа альтернативных проектов в условиях риска и информационной неопределенности. Эта разработка Российского экономического университета им. Г.В. Плеханова выгодно отличается от аналогов модульным построением, в основе которого лежит реализация алгоритмов моделей прямой и обратной иерархии, что позволяет проводить корректировку системы без существенных изменений внутри модулей. Кроме того, система Expert Solution 1.0 поддерживает алгоритмы расширения метода анализа иерархий – метода аналитических сетей [5]. Все это, вместе взятое, повышает эффективность принятия решения в условиях информационной неопределенности.

Разработка прикладных приложений позволила существенно упростить задачу обоснования рационального выбора инвестиционного проекта в условиях неопределенности среды, в которой реализуются проекты, с учетом влияния большого числа разнокачественных и трудноизмеримых факторов их эффективности.

В то же время это не решает ряд проблем, связанных с обоснованностью некоторых положений, лежащих в основе МАИ. Это относится, в частности, к процедуре свертки локальных приоритетов альтернатив в глобальный вектор (что является основой при решении многокритериальных задач) на основе использования матрицы парных сравнений. В случае многих критериев – а это является одной из важнейших особенностей данного подхода – глобальный вектор приоритетов рассчитывается по МАИ как аддитивная свертка локальных векторов приоритетов альтернатив. Именно это положение явилось элементом критики метода анализа иерархий. Так, В.Д. Ногин считает, что аддитивная свертка в МАИ не является корректной постольку, поскольку измерения приоритетов элементов иерархической модели осуществляются в шкале отношений, следовательно, необходимо использовать другой вид свертки локальных векторов приоритетов альтернатив – мультипликативный. В работе [2] он приводит такой «контрпример»: решается задача приобретения прямоугольного участка земли для последующего строительства дома. Имеются следующие три варианта: 100´100, 50´200 и 70´150, где измерение производится, например, в метрах. Однако ни при каких положительных весах критериев w1 и w2 (длины и ширины), вариант 70´150 не может оказаться выбранным (то есть иметь наибольший вес), если выбор осуществляется на основе МАИ.

На наш взгляд, этот пример характеризуется определенной некорректностью и не отвечает принципам метода анализа иерархии: длина и ширина участка не могут рассматриваться как критерии экспертного выбора. Однако с теоретической точки зрения вопрос о выборе рациональной формы свертки приоритетов правомерен.

В связи с этим нами выполнен имитационный эксперимент, цель которого – сравнить два альтернативных вида свертки – аддитивную и мультипликативную. В основу этого эксперимента положена иерархическая модель риск-анализа трех альтернативных проектов в сфере автомобилестроения с условными названиями Ford Focus II, KIA Rio 2 и «Тойота Камри» по уровню каждого из пяти факторов риска – финансового, риска сбыта, политического, производственного и рыночного риска [7].

В экспертно-аналитической системе Expert Solution 1.0 задача риск-анализа альтернативных проектов по пяти факторам риска сводится к генерации концептуальной иерархической модели, на верхнем уровне которой цель – фокус «оценка риска проектов», на среднем – факторы риска (финансовый риск, риск сбыта, политический, производственный и рыночный риски), на нижнем – сравниваемые проекты. Затем эксперту предъявляется матрица парных сравнений – критериев (факторов риска), затем пять матриц парных сравнений альтернатив (по каждому из факторов риска). Матрицы заполнены единицами, что отвечает их равной значимости, и эксперт на выплывающей шкале сравнений выбирает суждение о фактическом соотношении значимости критериев и альтернатив.

Результатом опроса является информационная модель риск-анализа по каждому из экспертов, одна из которых представлена на рис. 1.

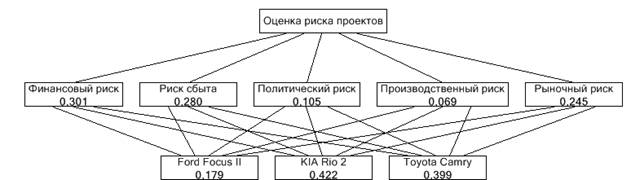
Рис. 1. Информационная модель риск-анализа альтернативных проектов (получена в системе Expert Solution 1.0)

На рис. 1 представлены глобальные приоритеты альтернатив, рассчитанные по аддитивной свертке локальных приоритетов. В программном пакете SPSS Base [8] рассчитаем векторы глобальных приоритетов альтернатив по двум видам свертки – мультипликативной и аддитивной – на основе данных по векторам локальных приоритетов.

Таблица 1

Расчет глобальных векторов уровня риска проектов

Полученные результаты, приведенные в двух последних строках таблицы, показывают, что эти векторы различаются, но ненамного, и ранжирование альтернативных проектов по уровню риска остается тем же. Оценим разницу между глобальными векторами риска проектов, вычисленными по формулам аддитивной и мультипликативной свертки, количественно. Автор метода анализа иерархий Т. Саати в работе [4] приводит две меры отклонения между векторами: среднеквадратичное отклонение (СКО) и медианное абсолютное отклонение (МКО), при этом отмечает, что для того, чтобы показать, насколько они малы в абсолютных значениях, их надо разделить на среднее значение приоритета, т.е. на 1/n, где n – число компонент вектора. Размерность глобальных векторов риска проектов n=3, отсюда значение меры отклонения (МО) по формуле среднеквадратического отклонения составит:

МО = {1/n Σ(w1i – w2i)2}1/2 / (1/n) = {1/3 [(0,179 – 0,187)2 + (0,422 – 0,429)2 + (0,399 – 0,384)2]}1/2 / (1/3) = 0,022.

Это значение меры отклонения меньше 0,1, и, по Т. Саати, можно считать, что оба вектора почти одинаковы.

Для оценки степени согласованности иерархий применим процедуру, предложенную в работе [4]. Степень согласованности информационной иерархической модели определяется величиной отношения согласованности OC

OC = Icoord / Ierr, (1)

где индекс согласованности Icoord рассчитывается по формуле

Icoord = (lmax - n) / (n - 1). (2)

Здесь lmax – максимальное собственное число матрицы парного сравнения, n — порядок матрицы, а Ierr — случайный индекс, т.е. индекс согласованности, сгенерированной случайным образом по шкале от 1 до 9 обратносимметрической матрицы с соответствующими обратными величинами элементов (значения Ierr приведены в [4]). Согласованность матрицы тем выше, чем меньше lmax отличается от ее размерности n.

Понятие согласованности в работе [4] обобщено на всю иерархию следующим образом: индексы согласованности, полученные из матриц парных сравнений альтернатив, умножаются на приоритеты критериев, относительно которых проведены сравнения, и к этому числу добавляется индекс согласованности матрицы парных сравнений важности рисков по отношению к цели. Затем эта величина сравнивается с соответствующим индексом, полученным как сумма случайно сформированных индексов, взвешенных соответствующими приоритетами.

Таким образом, описаны формулы оценки меры отличия глобальных векторов альтернатив, рассчитанных по разным формам свертки, и согласованности экспертных суждений. Это позволяет перейти к выявлению непосредственно связи меры отличия глобальных векторов рисков альтернативных проектов МО, вычисленной по формуле аддитивной и мультипликативной свертки, со степенью согласованности основной матрицы – матрицы парных сравнений факторов риска. Для решения этой задачи нами выполнен имитационный эксперимент, суть которого – в изменении элементов матрицы парных сравнений факторов риска в небольших пределах, на ±(1-2) делений девятибалльной шкалы отношений Т. Саати. Остальные пять матриц – матриц парных сравнений альтернативных проектов по каждому фактору риска при этом сохраняем неизменными.

Результаты имитационного эксперименты сведены в табл. 2, а на диаграммах рис. 2 зависимость различия векторов весов рисков проектов, рассчитанных по формулам аддитивной и мультипликативной свертки, от степени согласованности суждений в модели риск-анализа представлена в наглядном графическом виде.

Таблица 2

Результаты имитационного эксперимента по зависимости различия векторов весов рисков проектов, рассчитанных по формулам аддитивной и мультипликативной свертки, от степени согласованности суждений в модели риск-анализа

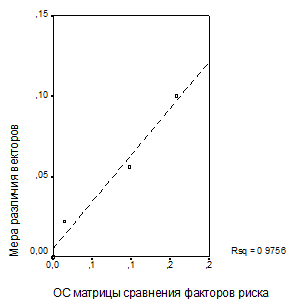а б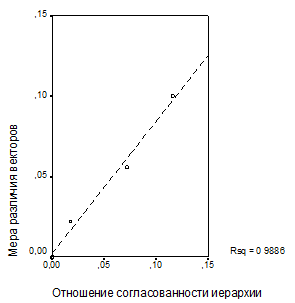

Рис. 2. Зависимость меры отличия векторов весов риска проектов, рассчитанных по формулам аддитивной и мультипликативной свертки: а – от отношения согласованности матрицы парных сравнений факторов риска; б – от отношения согласованности иерархии модели риск-анализа в целом

Из графиков на рис. 2 видно, что между мерой отличия векторов весов риска проектов, рассчитанных по формулам аддитивной и мультипликативной свертки, и показателями согласованности – отношением согласованности матрицы парных сравнений факторов риска, с одной стороны, и отношением согласованности иерархии модели риск-анализа в целом, с другой, наблюдаются тесные линейные зависимости.

Эти зависимости формально можно выразить следующими уравнениями:

МО = 0,00509 + 0,582 ´ ОС; (3)

МО = 0,00221 + 0,821 ´ ОСИ, (4)

где МО – мера отличия векторов весов риска проектов, рассчитанных по формулам аддитивной и мультипликативной свертки; ОС – отношение согласованности матрицы парных сравнений факторов риска; ОСИ – отношение согласованности иерархии модели риск-анализа в целом. При этом коэффициенты 0,582 и 0,821 в выражениях (3) и (4) отражают прирост меры различия векторов весов риска проектов, рассчитанных по формулам аддитивной и мультипликативной свертки, при увеличении предикторов на единицу.

По результатам имитационного эксперимента можно сделать выводы:

1) с ростом согласованности матриц парных сравнений различие глобальных векторов приоритетов альтернатив, рассчитанных по формулам аддитивной и мультипликативной свертки, уменьшается, и при достаточно высокой согласованности суждений по матрицам парных сравнений – не хуже ОС=0,10 – находится в допустимых пределах – не хуже 0,10;

2) выбор формы свертки локальных векторов приоритетов альтернатив в глобальный вектор практически не влияет на результаты ранжирования сравниваемых проектов.

Из выше написанного следует, что обеспечение условия согласованности экспертных суждений позволяет обеспечить устойчивость результата ранжирования альтернатив к выбору формы свертки локальных приоритетов, тем самым повысив качество управленческих решений.

Рецензенты:

Тихомиров Н.П., д.э.н., профессор, заведующий кафедрой математических методов в экономике ФГБОУ ВПО «Российский экономический университет имени Г.В. Плеханова» Министерства образования и науки РФ, г. Москва.

Колоколов В.А., д.э.н., профессор, профессор кафедры управления проектами и программами ФГБОУ ВПО «Российский экономический университет имени Г.В. Плеханова» Министерства образования и науки РФ, г. Москва.