Процесс горячего прессования композиционного древесного материала представляет собой контактный нагрев влажного пористого тела. Перенос тепла внутри пакета происходит теплопроводностью и конвекцией вследствие движения парогазовой смеси. Кроме того, значительное влияние на процессы переноса оказывают фазовые переходы (кипение – конденсация), именно это налагает дополнительные большие трудности на расчёт тепло- и массопереноса внутри прессуемого пакета.

Явления переноса энергии и вещества при нагреве влажных пористых тел подчиняются общим закономерностям термодинамики необратимых процессов [2].

В случае использования потенциала влагопереноса θ закон переноса массы имеет вид:

Используя выражение (1) и уравнения сохранения энергии и массы веществ, а также полагая коэффициенты переноса и термодинамические характеристики процесса постоянными и считая равными температуру скелета тела и связанного вещества, А.В. Лыков и Ю.А. Михайлов сформулировали систему дифференциальных уравнений тепломассопереноса [3].

Данная система может быть решена для граничных условий I, II и III рода, например, методами конечных разностей или сеточными методами [4 – 8]. Важно отметить, что численные методы решения систем дифференциальных уравнений в частных производных (ДУЧП) теплообмена (ТМО) при всей их глубокой проработанности и достаточной простоте реализации, имеют два существенных недостатка:

- отсутствие общего вида решения, а значит, и отсутствие в решении задачи физического смысла, что не позволяет к тому же проверить правильность решения;

- наличие явления неустойчивости решения, связанного с ошибками округления и являющегося свойством самой системы конечно-разностных уравнений.

Однако справедливости ради следует отметить, что системы ДУЧП ТМО с переменными теплофизическими характеристиками не имеют аналитического решения. В этой связи были предложены несколько другие модели процесса тепло- и массопереноса в пористых телах при высокотемпературном контактном нагреве.

Так в 70-е – 80-е годы была достаточно проработана теория прессования древесностружечных плит, разработанная А.Н. Обливиным и его учениками [1,9,10]. При некоторой корректировке данная теория может быть эффективно использована для анализа процесса горячего прессования широкого круга композиционных материалов, в том числе и на порошковых связующих. При этом необходимо учитывать, что количество влаги, вносимое со связующим в прессуемый пакет очень невелико. Следовательно, можно ожидать, что давление парогазовой смеси будет ощутимо меньше, чем при прессовании древесностружечных плит. Очевидно, что это приведёт к некоторому снижению интенсивности процессов тепломассопереноса в пакете и, как следствие, к снижению интенсивности отверждения связующего.

В порах пакета перенос энергии определяется механизмом конвекции, причем также с учётом тепловых эффектов, сопровождающих процессы испарения и конденсации на поверхности пор. Уравнение переноса энергии для паровоздушной смеси можно записать в следующем виде:

где

- коэффициент теплопроводности паровоздушной смеси, Вт/м·0С.

Окончательно система может быть записана в следующем виде:

1. Уравнения фильтрации:

2. Уравнение переноса паровоздушной смеси:

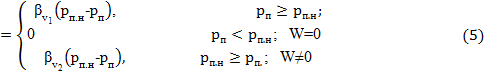
3. Уравнение влагосодержания:

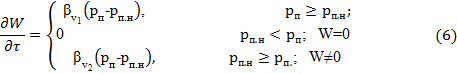
4. Уравнение теплопроводности в скелете пористого тела:

5. Уравнение переноса энергии паровоздушной смесью:

и алгебраические соотношения

Приведённая выше система уравнений описывает характерные особенности процессов тепло- и массообмена во влажном пористом теле для широкого класса режимов. Каждый конкретный режим задаётся определёнными краевыми условиями, а следовательно, решение системы (3) – (9) для конкретного режима – единственное.

Рассмотрим решение системы (3) – (9) для следующего режима прессования (табл. 1).

Таблица 1

Режим прессования композиционного материала

Решение системы ДУЧП проведено при следующих значениях параметров [1] (табл. 2).

Таблица 2

Исходные данные для решения задачи тепломассопереноса

Результаты решения приведены на рис. 1 – 4.

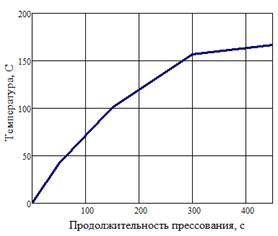
Рис. 1. Изменение температуры во времени в центре прессуемого пакета

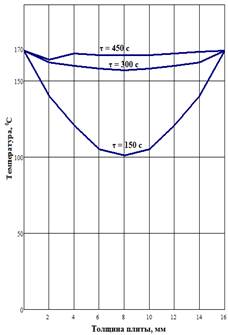
Рис. 2. Распределение температуры по сечению пакета в различные моменты времени

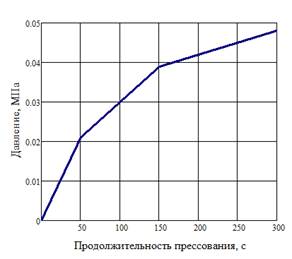
Рис. 3. Изменение давления во времени в центре прессуемого пакета

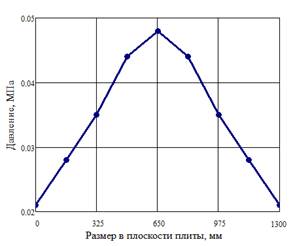
Рис. 4. Распределение давления в плоскости плиты

Анализ результатов решения системы ДУЧП тепломассопереноса позволяет заключить следующее:

1. Давление парогазовой смеси в прессуемом пакете достигает примерно вдвое меньшей величины, чем его аналогичные значения при прессовании древесностружечных плит [10] (см. рис. 3 – 4). На наш взгляд, это обусловлено тем, что имеющееся в прессуемом пакете количество влаги также примерно вдвое меньше.

2. Ожидаемое время достижения максимальных величин давления парогазовой смеси в центре пакета также существенно (примерно втрое) больше, чем при прессовании древесностружечных плит в аналогичных условиях [10] (см. рис. 3).

3. Градиент давления в плоскости плиты также не значителен по сравнению с прессованием древесностружечных плит (Pmax/Pmin = 2,3) (см рис. 4).

4. Всё, сказанное выше, позволяет заключить, что малые величины давления парогазовой смеси и его градиента обусловливают незначительный перенос тепла в плоскости плиты за счёт конденсации и конвекции, что приводит к довольно существенному увеличению времени прогрева прессуемого пакета (см. рис. 1 и 2). Поэтому, с одной стороны, можно прогнозировать существенное уменьшение такой составляющей цикла прессования, как продолжительность снижения давления, вплоть до практически полного его исключения. В свою очередь при прочих равных условиях это позволит увеличить производительность прессового оборудования.

С другой стороны, снижение интенсивности прогрева пакета приведёт к соответствующему снижению скорости отверждения связующего, что потребует увеличения времени выдержки прессуемого пакета под давлением.

5. Для детального решения описанных проблем необходимо провести экспериментальные исследования.

Рецензенты:

Черемных Н.Н., д.т.н., профессор, заведующий кафедрой Начертательной геометрии и машиностроительного черчения «Уральский государственный лесотехнический университет», г. Екатеринбург.

Уласовец В.Г., д.т.н., профессор кафедры механической обработки древесины ФГБОУ ВПО « Уральский государственный лесотехнический университет», г. Екатеринбург.