Введение
При построении автономных систем электроснабжения с использованием ветроэнергетических установок (ВЭУ) необходимо решить множество технических проблем, связанных с выбором рационального соотношения мощностей генерирующих и аккумулирующих источников, настройкой системной автоматики, оптимизацией параметров систем управления и т.п. Большинство этих задач можно решить только на основе моделирования рабочих режимов ВЭУ, для чего необходима динамическая модель ветра.
Использование сложных многомерных моделей ветра, построенных на дифференциальных уравнениях Навье-Стокса, описывающих движение нестационарного воздушного потока в пространстве и времени, для обозначенных задач исследования представляется избыточным.
С позиций ветроэнергетики наибольший интерес представляет продольная составляющая скорости ветра, моделированию которой и посвящена настоящая работа. Целью настоящих исследований является разработка универсальной модели динамической составляющей скорости ветра, пригодной для реализации в популярных математических пакетах.
Теоретическое обоснование
Колебания во времени основных метеорологических факторов, таких как скорость ветра, давление, влажность и т.д., содержат составляющие от долей секунды и по меньшей мере до десятков тысячелетий. С точки зрения моделирования рабочих режимов ВЭУ практический интерес представляют временные интервалы от секунд до нескольких часов.
Микрометеорологические колебания скорости ветра с периодами от долей секунды до минут определяются мелкомасштабной турбулентностью. Ее энергетический спектр в приземном слое атмосферы имеет максимум в периоде, порядка 1 мин.
В мезометеорологическом временном интервале с периодами от минут до часов интенсивные колебания метеорологических элементов относительно редки. Это позволяет получить относительно устойчивые средние значения скорости ветра, температуры и т.д., используя осреднение по периодам 10-20 мин.
На рис. 1 представлено спектральное распределение горизонтальной скорости ветра, построенное Ван-дер-Ховеном по данным измерений на 125-метровой метеорологической башне в Брукхэйвене [2; 5].
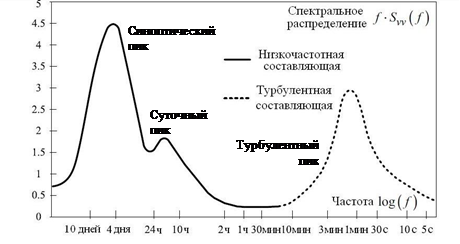
Рис. 1. Спектр горизонтальной скорости ветра
Из графика видно, что частота энергетического спектра синоптических и суточных колебаний скорости ветра существенно отличается от высокочастотных колебаний турбулентности, что позволяет использовать для их математического описания независимую временную дискретизацию с последующим наложением.
При принятых допущениях временная модель ветра может быть представлена в виде уравнения:
![]() , (1)
, (1)
где ![]() - средняя скорость ветра в 10-минутном временном интервале;
- средняя скорость ветра в 10-минутном временном интервале; ![]() - динамическая или турбулентная составляющая скорости ветра.
- динамическая или турбулентная составляющая скорости ветра.
Для статистического описания турбулентной составляющей скорости ветра в ветроэнергетике преимущественно используют эмпирические модели спектральной плотности S(f), наиболее известными из которых являются функции Давенпорта, Кармана и Каймала [1]. Для моделирования динамической составляющей скорости ветра в настоящей работе использовалась спектральная модель Каймала, рекомендованная международным стандартом [4].
В соответствии с моделью нормальной турбулентности предполагается, что турбулентные флюктуации скорости ветра являются стационарным полем случайных векторов, составляющие которого имеют гауссово статистическое распределение с нулевым математическим ожиданием.
Спектральные плотности мощности составляющих в нормализованном виде для модели Каймала описываются уравнением:
![]() , (2)
, (2)
где f - частота, Гц; S(f) - односторонний спектр продольной составляющей вектора скорости; σ - среднеквадратичное отклонение продольной составляющей вектора скорости; L - интегральный масштабный параметр турбулентности.
Спектральное разложение изображает стационарную случайную функцию разложенной на гармонические колебания различных частот f1, f2, .. fk,…, при этом амплитуды гармоник являются случайными величинами.
Согласно теореме Фурье любую функцию с периодом p можно представить в виде ряда:
![]() , (3)
, (3)
где Ak - амплитуда k-го гармонического колебания; ωk - круговая частота гармонического колебания; jk - начальная фаза k-го колебания; А0 – свободный член, представляющий собой математическое ожидание функции на интервале p.
С другой стороны, дисперсия стационарной случайной функции равна сумме дисперсий всех гармоник ее спектрального разложения:
![]() , (4)
, (4)
Если использовать один и тот же набор частот для спектрального разложения функции и ряда Фурье, то из (3)-(4) следует, что амплитуда k-го гармонического колебания ряда Фурье будет равна среднеквадратическому отклонению соответствующей гармоники спектра:
![]() , (5)
, (5)
где ∆f – расстояние между соседними частотами.
Выполнив несложные преобразования и перейдя к конечному числу частот N, получим уравнение для продольной составляющей скорости ветра, определенной на временном интервале Т:
![]() , (6)
, (6)
где ![]() - скорость ветра, осредненная на 10-минутном временном интервале.
- скорость ветра, осредненная на 10-минутном временном интервале.
В выражении (6) время моделирования Т соответствует полупериоду основной гармоники: Т= p, соответственно число N определяет частоту дискретизации временного сигнала:
![]() , (7)
, (7)
Выражения (2)-(6) позволяют построить имитационную временную модель продольной составляющей скорости ветра, если известны спектральные параметры турбулентности.
Величина спектральной плотности для соответствующей частоты fk определяется из уравнения (2), а фазовый угол jk представляет собой случайное число в диапазоне от 0 до 2p.
Спектральные параметры турбулентности для модели Каймала определяются в соответствии с требованиями, заданными в [4], согласно которым все ветроэнергетические установки по интенсивности турбулентности подразделяются на три подкласса А, В, С, каждый из которых характеризуется своим ожидаемым значением интенсивности турбулентности воздушного потока на высоте оси ветроколеса Iref.
Класс A соответствует ВЭУ с повышенной турбулентностью (Iref=0,16) и принимается для урбанизированной местности, в которой шероховатость земной поверхности составляет z0>0,3 [3]. Класс B соответствует более открытой местности (0,1<z0<0,3), и интенсивность турбулентности для него принимается равной Iref=0,14. Класс С характеризуется открытой местностью (z0<0,1) с интенсивностью турбулентности Iref=0,12.
Среднеквадратическое отклонение продольной составляющей скорости ветра на высоте оси ветроколеса для 90% квантиля и стандартных классов ВЭУ задается выражением:
![]() , (8)
, (8)
где ![]() - средняя скорость ветра на оси вращения ветроколеса.
- средняя скорость ветра на оси вращения ветроколеса.
Продольный масштабный параметр турбулентности воздушного потока ![]() на высоте оси ветроколеса Z выражается зависимостью:
на высоте оси ветроколеса Z выражается зависимостью:
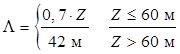 , (9)
, (9)
Для вычисления интегрального масштабного параметра продольной составляющей вектора скорости L используется выражение:
![]() . (10)
. (10)
Исходными данными для расчета параметров турбулентности являются класс ВЭУ, который определяется местом ее размещения, высота оси вращения ветроколеса Z и средняя скорость ветра для данного временного интервала моделирования ![]() .
.
Практическая реализация
Программная реализация представленной выше модели осуществляется в два этапа. На первом этапе рассчитываются значения амплитуд Ak и фазовых углов jk соответствующих гармоник моделируемого сигнала, а на втором этапе осуществляется его синтез.
Для выполнения вычислений необходимо создать два числовых массива данных: один размерностью M1[m,N], второй M2[N,Nt].
Параметр m в массиве М1 определяется количеством рассчитываемых переменных: fk, S(fk), Ak и т.п. Величина N определяет число гармонических колебаний, которые учитываются при разложении функции. При малой величине N получим невысокую точность расчета, большая величина N требует дополнительных ресурсов. Для решаемого класса задач вполне приемлемым представляется выбор числа учтенных гармоник, порядка N=100.
Параметр Nt соответствует заданному числу расчетных точек процесса, используемых для вывода. Важно отметить, что синхронизация частот, принятая при разработке модели, требует выполнения определенных соотношений между N и Nt.
Например, целью моделирования является имитация продольной составляющей скорости ветра на временном интервале Тмод=100 с. с дискретизацией ∆tзад=1 с. Если непосредственно принять Т=100 с., то при N=100 по выражениям (7) получим ∆t=1 с., что намного превышает желаемый интервал дискретизации.
Для данного примера необходимо определить период разложения, как Т=∆tзад∙N, после чего рассчитать параметр с, который определяет размерность выходного массива Nt=с∙N и число циклов расчета, которые необходимо выполнить для его полного заполнения:
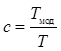 , (11)
, (11)
Нормированная спектральная плотность по Каймалу, определяемая по выражению (2), представлена в графическом виде на рис. 2.
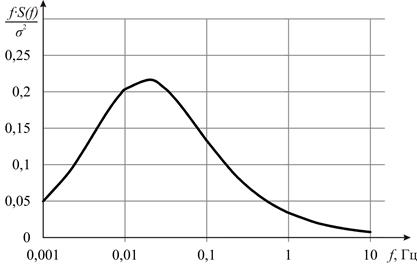
Рис. 2. Спектральная плотность по Каймалу
На рис. 3 приведен пример моделирования продольной составляющей скорости ветра по разработанной методике.
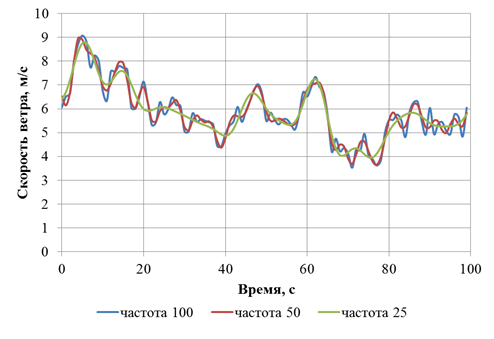
Рис. 3. Результаты моделирования
Выводы
Полученные результаты моделирования хорошо согласуются с результатами исследований других авторов, занимающихся разработкой математических моделей ветра для ветроэнергетики. Предлагаемая модель имеет простую структуру, легко реализуется средствами простых прикладных программ и может найти практическое применение в научных исследованиях, посвященных малой ветроэнергетике.
Работа выполнена в рамках государственного задания Министерства образования и науки РФ по приоритетным направлениям науки и техники (регистрационный номер НИР 7.5245.2011; номер государственной регистрации 01201254010 от 15.03.2012).
Рецензенты:
Кабышев А.В., д.ф.-м.н., профессор, кафедра «Электроснабжение промышленных предприятий» Энергетического института ФГБОУ ВПО «НИ ТПУ», г. Томск.
Лукутин Б.В., д.т.н., профессор, кафедра «Электроснабжение промышленных предприятий» ФГБОУ ВПО «НИ ТПУ», г. Томск.



