Введение

Раздел науки «идентификация аномалий» (anomaly detection) получил большое распространение за рубежом. К этому разделу относят различные математические аппараты, которые могут применяться для обнаружения отклонений от нормального состояния исследуемого объекта или системы. В этой области выделяют несколько основных направлений: статистические методы, экспертные системы, методы на основе нейронных сетей [8].

Одним из направлений применения данных математических технологий – это контроль и диагностика состояния объекта, при которых возникшая аномалия (отклонение от нормального состояния) системы свидетельствует о существующей неисправности в ней. Сравнительный анализ трех основных разделов идентификации аномалий, представленный в [8] показал, что применение нейронных сетей для решения задачи диагностики наиболее предпочтительно. Ранее был разработан алгоритм диагностики высоковольтного коммутационного оборудования [4], основанный на применении аппарата вейвлет-анализа и нейронных сетей. Однако, в работе [5] были описаны существенные недостатки совместного применения вейвлет-анализа и нейронных сетей: большие объемы данных, долгое время обучения, и, следовательно, относительно большое время идентификации неисправностей и значительные затраты вычислительных ресурсов.

Был предложен двухэтапный алгоритм диагностики, представленный на рис. 1 [2, 3].

Рис. 1. Двухэтапный алгоритм для диагностики высоковольтного коммутационного оборудования

В представленном алгоритме описанные выше недостатки применения нейронных сетей к задаче диагностики высоковольтного коммутационного оборудования решаются разделением процесса диагностики на два этапа (рис. 1). В первом этапе диагностики осуществляется идентификация неисправности по временным параметрам высоковольтного выключателя (собственное время отключения, полное время отключения и собственное время включения, разновременность включения фаз). На втором этапе нейронная сеть определяет вид неисправности по рассчитанному вейвлет-спектру скоростной характеристики. Переход ко второму этапу диагностики осуществляется после подтверждения первым этапом наличия какой-либо неисправности (обнаружения отклонений от нормального состояния).

В данной статье проводится сравнительный анализ применения на первом этапе алгоритма диагностики высоковольтного коммутационного оборудования статистической классификации и экспертной системы, построенной на базе нечеткой модели временных параметров высоковольтного коммутационного аппарата. Приводятся зависимости выхода нечеткой и статистической моделей (исправность/неисправность выключателя) от полученных входных переменных. Демонстрируются статистическая и нечеткая модели, построенные в пакете математического моделирования Matlab.

Цель работы: сравнительный анализ статистической и нечеткой моделей диагностики высоковольтного коммутационного оборудования по временным параметрам.

Материал и методы исследований: диагностика высоковольтных выключателей, статистическая классификация, нечеткая логика, математическое моделирование с использованием системы для математических вычислений Matlab.

Результаты и обсуждение

Для сравнительного анализа статистической и нечеткой моделей высоковольтного коммутационного аппарата был выбран высоковольтный выключатель ВПМ-10-20/630 У3 со следующими характеристиками [1]:

Номинальное напряжение, кВ: 10;

Наибольшее рабочее напряжение, кВ: 12;

Номинальный ток, А: 1000;

Номинальный ток отключения, кА: 20;

Номинальный ток включения, кА: 52;

Собственное время отключения, мс: 120;

Полное время отключения, мс: 140;

Собственное время включения, мс: 300.

Основными параметрами для сравнения выбираются сложность построения модели, ее адекватность, скорость обработки новых данных.

В качестве параметров для построения нечеткой модели были выбраны собственное время отключения, полное время отключения и собственное время включения. Учитывая номинальные значения этих параметров, в нечеткой модели были заданы следующие возможные диапазоны их изменения:

Собственное время отключения (t.own.off), мс: 110-130;

Полное время отключения (t.complete.off), мс: 130-150;

Собственное время включения (t.own.on), мс: 290-310.

Также к этим трем основным параметрам были добавлены еще шесть дополнительных параметров, учитывающих разность во времени срабатывания фаз 1-2 (t.1-2.off), 2-3 (t.2-3.off), 3-1 (t.3-1.off) отключения и 1-2 (t.1-2.on), 2-3 (t.2-3.on), 3-1 (t.3-1.on) включения. Для этих шести параметров принят диапазон изменения 0-20 мс .

Для нечеткой модели были использованы треугольные функции принадлежности, оператор пересечения – MIN, оператор объединения – MAX [9].

С использованием описанных переменных экспериментальным путем были построены нечеткие правила:

1. Если t.own.off=120 И t.complete.off=140 И t.own.on=300 И t.1-2.off=0 И t.2-3.off=0 И t.3-1.off=0 И t.1-2.on=0 И t.2-3.on=0 И t.3-1.on=0 ТО выключатель исправен.

2. Если t.own.off=110 ИЛИ t.complete.off=130 ИЛИ t.own.on=290 ИЛИ t.1-2.off=20 ИЛИ t.2-3.off=20 ИЛИ t.3-1.off=20 ИЛИ t.1-2.on=20 ИЛИ t.2-3.on=20 ИЛИ t.3-1.on=20 ТО выключатель неисправен.

3. Если t.own.off=130 ИЛИ t.complete.off=150 ИЛИ t.own.on=310 ИЛИ t.1-2.off=20 ИЛИ t.2-3.off=20 ИЛИ t.3-1.off=20 ИЛИ t.1-2.on=20 ИЛИ t.2-3.on=20 ИЛИ t.3-1.on=20 ТО выключатель неисправен.

Работа полученной модели была смоделирована на графическом программном языке Simulink [6] (см. рис. 2). Данная модель может быть использована при построении интеллектуальных диагностических систем различных типов коммутационного оборудования электрических подстанций.

Рис. 2. Моделирование работы нечеткой модели в программной среде Simulink

Особенности построения нечеткой модели:

- отсутствует необходимость в библиотеке примеров;

- необходимо наличие априорной информации об объекте, заключающееся в кратком описании эксперта о примерных уровнях значений анализируемых параметров.

Алгоритм построения статистической модели обнаружения аномалий следующий [7]. Выбирается библиотека значений x, которые принимают аномальные значения. Затем на основании значений x рассчитываются математическое ожидание μ и дисперсия σ2 по следующим формулам:

,

,

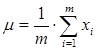где m – количество значений x в библиотеке, i – номер элемента x из библиотеки.

Затем рассчитывается вероятность появления комбинации анализируемых параметров 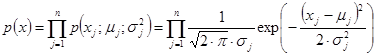, где n – количество анализируемых параметров x, j – номер параметра x из библиотеки.

Рис. 3. Зависимость вероятности появления комбинации параметров время включения (tвкл) и время отключения (tвыкл) от значений этих параметров

Устанавливается пороговое значение ε. Если условие p(x) > ε не выполняется, то имеет место аномалия, в данном случае, в исследуемом объекте присутствует неисправность.

У статистического метода имеется ряд особенностей:

- необходимо наличие небольшого количества положительных примеров для построения модели;

- большое количество отрицательных примеров (с присутствием аномалии) для построения модели;

- наличие статистической информации об анализируемых параметрах;

- различает большое количество аномалий, соответственно неисправностей.

В таблице 1 приведены временные параметры работы обоих моделей.

Таблица 1.

Анализ полученных моделей на примере высоковольтного выключателя ВПМ-10-20/630 У3 позволил сделать следующие выводы.

Выводы

1. «Интеллектуализация» диагностических систем позволяет на основе эмпирического опыта с легкостью автоматизировать довольно сложные системы. В частности, применение нечеткой логики уменьшает вычислительные затраты в связи с использованием приближенных вычислений. Однако в случае, когда нечеткое моделирование можно заменить несколькими несложными формулами расчета вероятности, по скорости выполнения статистическая модель становится предпочтительной.

2. Как статистическая, так и нечеткая модели правильно выделяли аномальные примеры при тестировании, поэтому обе модели по точности диагностики находятся на одном уровне.

3. Статистическая модель в связи с особенностью построения наиболее предпочтительна к применению в случаях, когда имеется библиотека примеров с заранее известными статистическими параметрами, в частности, вероятностью получения значения данного параметра.

4. Нечеткая модель становится предпочтительной в случае отсутствия статистического описания объекта, при наличии подготовленного экспертом его априорного описания.

Статья подготовлена по результатам работ, полученным в ходе выполнения проекта № СП-1967.2013.1, реализуемого в рамках программы "Стипендии Президента Российской Федерации молодым ученым и аспирантам, осуществляющим перспективные научные исследования и разработки по приоритетным направлениям модернизации российской экономики".

Рецензенты:

Горбатенко Н.И., д.т.н., профессор, первый проректор, ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова», г.Новочеркасск.

Колпахчьян П.Г., д.т.н., профессор кафедры "Электромеханика и электрические аппараты", ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова», г.Новочеркасск.