Введение
Для проведения горных выработок широко применяются проходческие комбайны избирательного действия, имеющие различные типы погрузочных органов. В последнее время широкое распространение находят погрузочные органы с нагребающими звездами, отличающиеся простотой конструкции, повышенной надежностью. Однако такие погрузочные органы недостаточно изучены [5]. Физические процессы погрузки горной массы отличаются от подобных для погрузочных органов с нагребающими лапами вследствие существенно различной конструкции и характера движения исполнительных элементов в штабеле горной массы (траектории, скорости, формы элементов).
Цель исследований
Целью работы является повышение эффективности эксплуатации проходческих комбайнов избирательного действия с нагребающими звездами путем выбора рациональных параметров погрузочных органов для заданных условий эксплуатации на основе изучения процессов взаимодействия с разрушенной горной массой.
Для достижения цели решены следующие задачи:
1) проведены экспериментальные исследования на модели погрузочного органа с нагребающими звездами различной конфигурации для изучения влияния геометрических параметров на производительность погрузки и сопротивления зачерпыванию;
2) проанализирован процесс взаимодействия погрузочных органов со штабелем горной массы, на основе чего построены математические модели и алгоритмы расчета рабочего процесса;
3) разработана инженерная методика выбора параметров погрузочного органа.
Экспериментальны исследования
При разработке методики экспериментальных исследований [2] были учтены основные особенности формирования объёма единичного черпания, который определяет производительность погрузочного органа и комбайна в целом, а также сопротивления зачерпыванию горной массы.
Экспериментальные исследования позволили установить [1, 2, 6] влияние следующих факторов на формирование производительности и нагрузок в приводе нагребающих звезд: количество лучей нагребающей звезды Z (угол развала лучей β), угол установки Θ, высота h, длина l лучей (зависит от диаметров звезды r и центальной втулки r1 соответственно) и частота вращения нагребающей звезды n. Высота штабеля и крупность материала принята постоянной, соответствующей средним производственным данным; угол наклона питателя — 20º, что соответствует, например, проходческому комбайну КП-21 и другим.
Структура математической модели производительности
Как показали исследования, производительность погрузочного органа зависит от конструктивных параметров нагребающей звезды, гранулометрического состава материала, представленного средним размером куска dsr, глубины внедрения погрузочного органа S, а также объема активной зоны материала штабеля Va [3, 4, 6]:
.
Процесс формирования объема захвата материала лучами нагребающих звезд подчиняется тем же основным закономерностям, что и нагребающие лапы шахтных погрузочных машин [7]. Однако, погрузочные органы с нагребающими звездами имеют существенные конструктивные особенности, влияющие на процесс погрузки. Признано целесообразным применить мультипликативную форму зависимости, что позволяет сохранить преемственность в известном подходе к расчету производительности и сопротивлений зачерпыванию. Теоретическую производительность нагребающей звезды можно выразить следующим соотношением [3]:
, м3/мин,
где 
- максимальная площадь захвата материала одним лучом нагребающей звезды в функции числа лучей, м2;
Km.h, Km.θ, Km.Z, Km.N — соответственно коэффициенты влияния относительной высоты луча, его угла установки и режима работы погрузочного органа (влияние глубины внедрения или номера черпания).
Структура математической модели нагрузок
Зависимость среднего значения момента сопротивления на валу нагребающих звезд за один оборот звезды по аналогии с нагребающими лапами зависит от массы захваченного материала, диаметра нагребающей звезды dzv и ряда факторов, учитываемых коэффициентами KM.h, KM.θ, KM.Z, KM.N:
, Н·м,
где γ - плотность материала, кг/м3;
g = 9,81 — ускорение свободного падения, м/с2.
Следует отметить, что, несмотря на аналогичные обозначения коэффициентов влияния различных факторов в моделях производительности и момента сопротивления, конкретные математические зависимости каждого из коэффициентов, как показано ниже, имеют различные математические выражения.
Геометрическое моделирование площади черпания
Для определения зависимости площади захвата материала лучом нагребающей звезды от конструктивных параметров (Z, Θ, dzv, r1) составлена расчетная схема (рис. 1) и проведено геометрическое моделирование нагребающей звезды.
Нагребающая звезда состоит из центральной втулки с прикрепленными на ней нагребающими лучами. Точки крепления лучей к втулке обозначены ai (где i=1..Z), края лучей bi описывают круговую траекторию при вращении нагребающей звезды.
Нагребающие лучи могут устанавливаться под углом Θ, имеющим знак минус при повороте луча против движения (на рис. 1 по часовой стрелке). Лучи на звезде устанавливаются равномерно и для определенности нумеруются по направлению вращения звезды. Угол поворота звезды φ соответствует углу поворота первого луча.
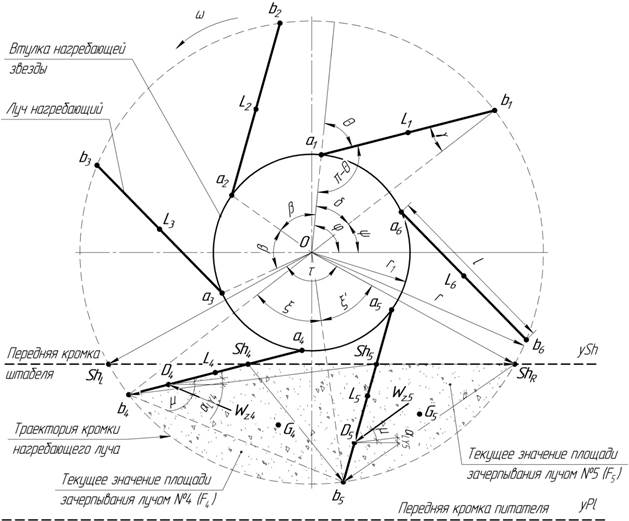
Рисунок 1 — Расчетная схема нагребающей звезды
В общем случае, решить задачу определения координат точек bi при любом угле поворота звезды φ можно рассматривая треугольник Oa1b1:
,
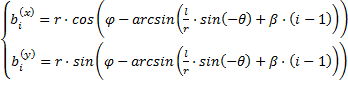где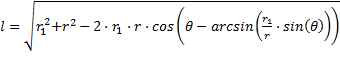 
- длина луча.
Для погрузки горной массы нагребающая звезда погружается в штабель горной массы на величину S, образуя, таким образом, геометрическую площадь захвата материала:
.
В отличие от погрузочного органа с нагребающей лапой [5, 7], нагребающая звезда имеет несколько нагребающих элементов. При сочетании определенной глубины внедрения рабочего органа в штабель горной массы и количества лучей возможны два принципиально различных варианта работы нагребающих лучей [2]:
1. В каждый момент времени в процессе черпания в штабеле находится только один луч. Данный вариант возможен при количестве лучей один, два, а также, при определенной глубине внедрения, три луча.
2. В каждый момент времени в процессе черпания в штабеле может находиться два и более лучей. Условие существования второго варианта работы лучей:
или 
.
Текущая площадь Fi захвата материала нагребающим лучом определяется как сумма площадей четырехугольника Shibibi+1Shi+1 и сегмента траектории, ограниченной хордой bibi+1:
.
Когда i+1 луч покидает штабель, площадь захвата определяется по формуле:
.
Для геометрического моделирования формирования площадей захвата лучей нагребающей звезды была написана программа на языке Python.
В результате моделирования установлено, что максимальная площадь захвата материала нагребающим лучом от угла установки лучей при постоянстве остальных параметров (Z, dzv, r1, S) не зависит. Незначительная разница в массах погруженного материала, установленная экспериментально, объясняется различной траекторией движения материала между лучами: при внедрении радиально установленного луча (Θ=0º) в штабель луч сдвигает первые куски по ходу движения, уплотняя материал перед собой и частично выдавливая его к центру звезды, что не наблюдается на лучах с Θ=-90º. Эта разница учитывается коэффициентами Km.Θ и KM.Θ.
Математические модели рабочего процесса
Обработка результатов экспериментальных исследований нагребающих звезд позволила установить зависимости массы погруженного материала и среднего момента сопротивления от высоты, угла установки, количества нагребающих лучей и порядкового номера черпания (режима работы погрузочного органа) (рис. 2).
Обработка результатов исследований нагребающих звезд позволила вывести зависимость массы погруженного материала за один определенный оборот звезды:
, кг
где Nzv — количество нагребающих звезд на погрузочном органе;
Km.h — коэффициент влияния относительной высоты луча:
;
- относительная высота луча;
- коэффициент влияния угла установки лучей;
- коэффициент влияния количества лучей на нагребающей звезде;
- коэффициент режима работы погрузочного органа.
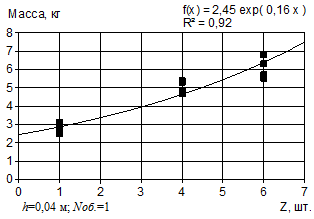
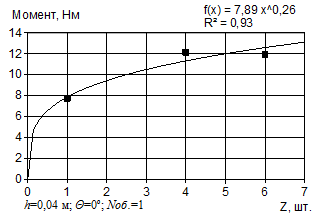
Рисунок 2 — Зависимости массы погруженного материала и среднего момента сопротивления от конструктивного исполнения нагребающей звезды и режима работы
Среднюю производительность погрузочного органа с двумя нагребающими звездами за первые N оборотов нагребающих звезд удобно представить в виде:
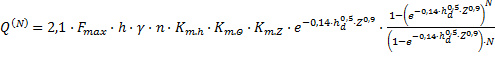, кг/мин.
Аналогично, анализируя зависимости среднего момента сопротивлений от конструктивных параметров и режима работы погрузочного органа (рис. 2), определены коэффициенты влияния математической модели момента сопротивлений.
Зависимость среднего значения момента сопротивления на нагребающих звездах погрузочного органа от захваченного материала за один определенный оборот звезды:
, Н·м,
где g = 9,81 — ускорение свободного падения, м/с2;
dz — диаметр нагребающей звезды, м;
— влияние относительной высоты луча;
- коэффициент влияния угла установки лучей;
- коэффициент влияния количества лучей на нагребающей звезде;
- коэффициент влияния режима работы погрузочного органа.
Средний момент сопротивления за первые N оборотов нагребающих звезд, учитывая количество звезд равное двум:
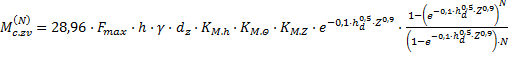, Н·м.
Оценка адекватности математических моделей
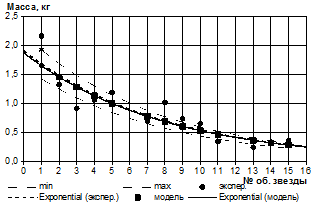
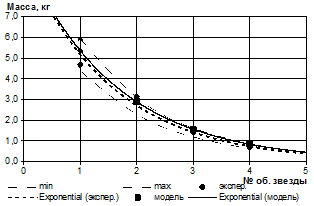
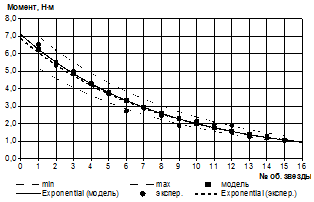
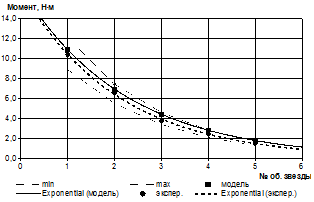
Относительная ошибка в определении массы погруженного материала и среднего момента сопротивления за один определенный оборот нагребающей звезды в сравнении с экспериментальными значениями в среднем не превышает 12 %, например, на рис. 3 и 4 приведены зависимости для модельных условий (коэффициент моделирования λ=3,5). Линии минимума и максимума соответствуют относительной ошибке в 15 %.
|
|
|
|
h=0,02 м; Θ=0º; n=24 об/мин; Z=1; dz=0,471 м |
h=0,04 м; Θ=-90º; n=24 об/мин; Z=4; dz=0,391 м |
Рисунок 3 — Оценка адекватности математической модели массы погруженного материала для разных конструктивных исполнений нагребающих звезд
|
|
|
|
h=0,04 м; Θ=-90º; Z=1; dz=0,391 м |
h=0,02 м; Θ=0º; Z=6; dz=0,471 м |
Рисунок 4 — Оценка адекватности математической модели среднего момента сопротивления для разных конструктивных исполнений нагребающих звезд
Энергоемкость процесса погрузки
При проектировании погрузочных органов проходческих комбайнов с нагребающими звездами для сравнения между собой различных вариантов удобно и значительно более информативно пользоваться не значениями производительности и нагрузок, а показателем энергоемкости:
, мВт·ч/кг.
Средняя энергоемкость за первые N оборотов нагребающих звезд:
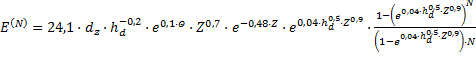, мВт·ч/кг.
В результате моделирования установлено, что наименьшей энергоемкостью процесса погрузки обладают нагребающие звезды с шестью лучами, установленными под углом -90º, несмотря на то, что наибольшую производительность показывают звезды с радиальными лучами (Z=6 и Θ=0º), а наименьшие нагрузки испытывают звезды с одним лучом.
Выводы
1. Разработанные математические модели производительности и нагрузок дают удовлетворительную сходимость с экспериментальными данными, полученными на модельной экспериментальной установке. Относительная ошибка не превышает 12 %.
2. Для проходческих комбайнов избирательного действия минимизация энергоемкости погрузки материала погрузочным органом при заданной производительности, определяемой производительностью разрушающего органа, позволяет достичь наилучших показателей работы всего проходческого комбайна.
3. Используя полученные математические модели можно выполнить оптимизацию параметров погрузочного органа, задавшись целевой функцией и системой ограничений.
Рецензенты:
Луганцев Б.Б., д.т.н., генеральный директор ОАО «Шахтинский научно-исследовательский и проектно-конструкторский институт», г.Шахты.
Евстратов В.А., д.т.н., профессор, декан Технологического факультета Шахтинского института (филиала) ЮРГПУ(НПИ) им. М.И. Платова, г.Шахты.