Введение
Со времени промышленной революции люди постоянно улучшают качество жизни человека, увеличивая возможности производства. Расширение производства приводит к увеличению потребления природных ресурсов и энергии, а также к проблемам утилизации непригодной к дальнейшему использованию продукции. В настоящее время масштабы индустриальной деятельности уже достигли предела и нельзя больше столь интенсивно истреблять ресурсы и энергию, а также избавляться от отходов, не принимая во внимание сильное воздействие этой деятельности на окружающую среду. Одним из путей выхода из сложившейся ситуации является переход от парадигмы производства – «Как произвести продукцию наиболее рациональным образом?» к парадигме – «Как избежать выпуска новой продукции и обеспечить удовлетворенность потребителя и корпоративные выгоды?» [1].
Цели новой парадигмы могут быть достигнуты за счет модернизации уже выпущенной продукции, поводом к проведению которой являются, как правило, изменения требований со стороны заказчика (потребителя) или общества. Под модернизацией объекта понимается его изменение, отвечающее современным требованиям [3].
Одно из направлений модернизации предприятий различных отраслей промышленности связано с унификацией технологических процессов, используемых для производства однотипных образцов продукции, и внедрение на этой основе типовых производственных процессов, что позволит снизить стоимость производства этой продукции. Для решения этой задачи требуются значительные финансовые средства, общий объем которых и объем средств, выделяемых каждому предприятию, необходимо строго обосновать.
В данной работе предлагается метод оптимизации затрат на государственные капитальные вложения при реализации проектов по внедрению типовых производств, разработанный на основе подходов, изложенных в [4].
Математическая постановка задачи определения функций отклика
Рассмотрим множество предприятий отрасли промышленности, выпускающих однотипную продукцию, выпуск которой обеспечивается некоторой совокупностью производственных процессов, технология реализации которых в настоящее время индивидуальна для каждого предприятия. Задачу будем решать в достаточно общей постановке, когда множество типовых производств, кандидатов на внедрение, имеет альтернативные варианты.
Непременным требованием к процессу внедрения типовых производств является достижение заданных результатов при минимальных издержках. Для разработки оптимальных в этом смысле планов финансового обеспечения процесса модернизации отрасли (в данном случае, внедрения типовых производств) необходимо знать, какой эффект будет получен от той или иной суммы вложений в работы по модернизации, т.е. к какому изменению показателей качества функционирования отрасли приведет их выполнение. Функцию, характеризующую эти изменения, назовем функцией чувствительности показателей качества функционирования отрасли к вложению средств на их модернизацию или, для краткости, функцией отклика.
В процессе мониторинга предприятий отрасли [1] для каждого однотипного образца продукции необходимо определить перечень типовых производств и их альтернативных вариантов, обеспечивающих его изготовление, в результате внедрения которых могут быть улучшены показатели качества функционирования отрасли. Каждое типовое производство из этого перечня должно характеризоваться затратами на его внедрение и вкладом в улучшение (ухудшение) названных показателей. Эта информация может быть использована в качестве исходных данных для последовательного определения соответствующих функций отклика показателей качества каждого образца продукции, качества функционирования каждого предприятия, входящего в состав отрасли, и отрасли в целом на внедрение типовых производств. Полученные функции отклика в свою очередь являются исходным материалом для решения задачи определения оптимального объема работ по внедрению типовых производств в масштабе отрасли, обеспечивающего требуемые значения показателей качества его функционирования при минимальных затратах. Рассмотрим последовательно математические постановки задач определения функций отклика и оптимального объема работ по модернизации предприятий отрасли применительно к структуре внедрения типовых производств представленной на рисунке 1.
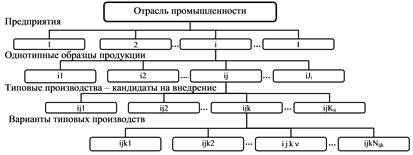
Рисунок 1 – Структура внедрения типовых производств на предприятиях отрасли
Обозначим:
I – количество модернизируемых предприятий отрасли;
Ji – количество типовых образцов, выпускаемых i-ым предприятием;
Kij – количество возможных типовых производств, которые могут быть применены в производстве j-го образца продукции i-го предприятия;
Nijk – количество альтернативных вариантов k-го типового производства j-го образца продукции i-го предприятия;
L – количество показателей качества функционирования образца продукции.
Исходные данные для решения задач определения функций отклика показателей качества образцов продукции целесообразно представить совокупностью таблиц, построенных для каждого образца и имеющих структуру, подобную структуре таблицы 1.
Таблица 1. Исходные данные для определения функций отклика показателей качества j-го типового образца продукции
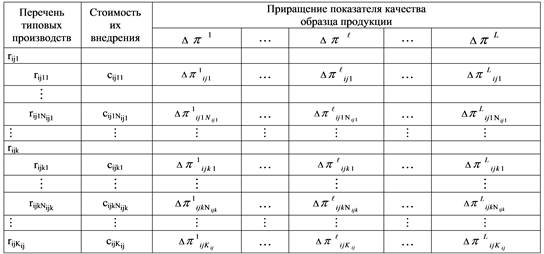
В таблице 1 типовые производства и их варианты упорядочены в порядке возрастания стоимости их внедрения и приняты следующие обозначения:
– условное наименование k-го типового производства (
) j-го образца продукции (
) на i-м предприятии (
);
– затраты на внедрение n-го варианта (
) ijk-го типового производства;
– приращение 
-ого показателя качества функционирования типового образца продукции (
) за счет внедрения ν-го варианта k-го типового производства j-го образца продукции, выпускаемой i-м предприятием.
Суммарное изменение показателей качества функционирования ij-го образца является некоторой функцией частных приращений этих показателей за счет внедрения ijk-го типового производства:
(1)
Функция (1) часто является аддитивной. Например, это имеет место для такого показателя как стоимость производства образца продукции. В этом случае функция (1) примет вид
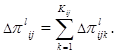
Тогда для решения задач определения функций отклика названных выше показателей может быть применен метод динамического программирования [2]. Названные задачи решаются последовательно: сначала определяются функции отклика, характеризующие чувствительность показателей качества образцов продукции, а затем на основе этих данных – показателей качества функционирования отдельных предприятий и, наконец, суммарная функция отклика. Сформулируем эти задачи.
В случае наличия в перечне типовых производств ij-го образца продукции альтернативных вариантов показатели их качества и ограничения на ресурсы, выделяемые на внедрение типовых производств, должны быть записаны в виде:
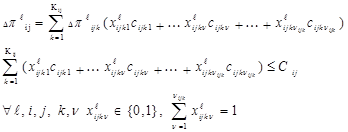
где Cij – возможное количество средств выделяемых на внедрение типовых производств ij-го типового образца. В этом случае первая задача может быть сформулирована следующим образом.
Задача 1.
Дано: зависимости 
, представленные таблично.
Найти:
для 
при условии, что 
где 
– вектор, характеризующий оптимальный объем работ по модернизации производства ij-го образца продукции при выделении для этой цели ассигнований в размере 
. Каждому элементу 
, равному 1, соответствует типовое производство 
, которое целесообразно внедрить, а элементы 
, равные нулю, указывают на то, что при данном уровне финансирования не целесообразно внедрение соответствующих им типовых производств ;
– точность распределения средств по работам плана модернизации производства ij-го образца продукции;
Так как задача решается для спектра значений , то в результате ее решения получим не только оптимальный объем работ по модернизации производства ij-го образца продукции, но и дискретную функцию 
, характеризующую чувствительность показателя качества функционирования i-го предприятия к вложению средств на модернизацию производства ij-го образца продукции. Эта функция используется при решении следующей задачи: определение функции отклика показателя качества функционирования отрасли на оптимальное вложение средств в модернизацию его объектов.
Задача 2.
Дано: зависимости , полученные в результате решения первой задачи.
Найти: для 
при условии, что 
где 
– возможное количество средств выделяемых на модернизацию i-го предприятия;
– вектор, элементы которого характеризуют оптимальный объем работ по модернизации i-го предприятия отрасли;
– точность распределения средств на модернизацию i-го объекта ОПК по видам оборудования.
Задача 3.
Дано: зависимости 
для каждого i-го объекта НКИ, полученные в результате решения предыдущей задачи.
Найти: для всех 
при условии 
где 
– вектор, элементы которого равны оптимальному количеству средств, необходимому для модернизации i-го объекта НКИ;
– точность распределения средств на модернизацию объектов НКИ.
Алгоритмы решения сформулированных задач основаны на использовании соответствующих им функциональных уравнений Беллмана и приведены в работе [4].
На этапе прямого хода алгоритма динамического программирования будут получены функции, характеризующие соответственно увеличение эффективности производства (в частности, экономической) отдельных образцов продукции, функционирования предприятий и отрасли в целом за счет оптимального использования средств на внедрение типовых производств, а на этапе его обратного хода – оптимальные варианты типовых производств.
Графическая иллюстрация алгоритма получения решения
Графическая иллюстрация алгоритма получения решения и возможностей его интерпретации приведена на рисунке 2. Алгоритм отражает следующую ситуацию:
- в отрасль входит 3 предприятия;
- на каждом предприятии выпускается по 2 образца продукции;
- при изготовлении каждого образца могут быть использованы два варианта типового производства.
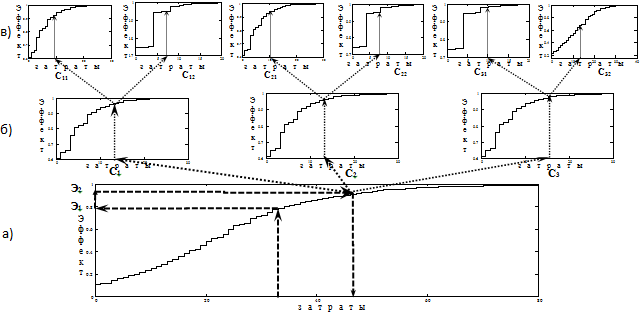
Рисунок 2 – Графическая иллюстрация алгоритма получения решения задачи методом динамического программирования и возможностей его интерпретации
Предположим, что на внедрение типовых производств на предприятий отрасли предполагается выделить ассигнования в объеме С1. Тогда, используя полученную зависимость увеличения показателя эффективности функционирования отрасли в целом за счет оптимального использования средств на внедрение типовых производств (рис. 2а), можно определить, какой эффект (например, размер годовой экономии) будет получен при использовании выделенных средств. Если этот эффект, в данном случае Э1, недостаточен и желательно получить эффект в размере Э2, то можно определить необходимый для этого объем ассигнований С2 и далее последовательно найти оптимальное распределение этого объема по предприятиям (рис. 2б) и образцам продукции (рис. 2в).
Заключение
В заключение отметим полезные особенности предложенного метода, выгодно отличающие его от других методов. К ним относятся:
- возможность получения спектра решений, что позволяет обосновать размер потребных инвестиций для модернизации отрасли промышленности и оптимально распределить выделенные средства между ее участниками.
- гарантированное нахождение абсолютного, а не локального экстремума, если задача многоэкстремальна. Кроме того, метод позволяет найти все множество решений задачи, при которых имеет место один и тот же экстремум. Наличие таких вариантов позволяет привлечь к рассмотрению дополнительные показатели качества модернизации.
- возможность распараллеливания вычислений, что может оказаться чрезвычайно полезным при решении крупномасштабных задач.
Таким образом, изложенная методика позволяет получить богатый материал для обоснования и принятия решения об объеме инвестиций в модернизацию отрасли промышленности и режиме финансирования работ, выполняемых на ее предприятиях.
Рецензенты:
Петров Г.Д., д.т.н., профессор, начальник кафедры, ВКА имени А.Ф.Можайского, г.Санкт-Петербург.
Миронов А.Н., д.т.н., профессор, начальник кафедры, ВКА имени А.Ф.Можайского, г.Санкт-Петербург.