Задача оптимизации распределения транспортных потоков по сети, несомненно, актуальна, и, несмотря на многочисленные исследования в этой области, по-прежнему еще требует решения [2]. Это связано с многочисленностью и, порой, противоречивостью параметров оптимизации; сложностью определения исходных данных для оптимизации; необходимостью привязки алгоритмов к конкретной транспортной сети и т.п. В данной работе приводятся исследования авторов по вопросу оптимизации параметров светофорного регулирования в узловых точках. Применение этих исследований на стадии проектирования сети или при реорганизации дорожного движения позволит избежать транспортных заторов на перекрестках.
Математическая модель задачи оптимизации параметров светофорного регулирования в узловой точке
Рассматривая транспортный поток как случайный процесс [1, 4], авторами ранее была разработана математическая модель движения автотранспортных средств по улично-дорожной сети и выведены аналитически функции для определения параметров качества организации движения при справедливости гипотезы о распределении интервалов по времени между транспортными средствами по обобщенному закону Эрланга [3].
Пусть 
– число потоков магистрали № 1; 
– число потоков магистрали № 2;
h – среднее время (в секундах) между пересекающими узловую точку требованиями одного потока;
– функция восстановления для i-го потока магистрали № 1;
– суммарная задержка всех требований i-го потока за один цикл регулирования;
Т1 – время, в течение которого запрещено движение для потоков магистрали № 1, с;
Т2 – время, в течение которого запрещено движение для потоков магистрали № 2, с;
T = T1+T2.
Суммарная задержка всех требований данного потока за единицу времени – один час, выражается следующим образом:
(треб.•ч)
Поставим следующую задачу оптимизации функционирования узловой точки типа «регулируемое пересечение потоков требований»: минимизировать суммарную часовую задержку всех требований в данном узле. Целевая функция:
(1)
В результате следует получить оптимальные значения параметров регулирования 
.
При этом для каждого потока должно выполняться условие отсутствия затора (т.е. при движении требований по данной полосе количество требований, прибывающих к УТ за один цикл, не превышает количества требований, пересекающих УТ за то время 
, когда движение разрешено):
, 
; (2)
, 
. (3)
Кроме этого необходимо выполнение условия:
, (4)
(5)
где М – минимальное время (в секундах), необходимое требованию для пересечения узловой точки типа «регулируемое пересечение потоков требований».
Теорема. Задача математического программирования (1)-(5) не имеет экстремума во внутренних точках области допустимых значений.
Доказательство
С учетом (5) получаем задачу математического (нелинейного) программирования (ЗМП):
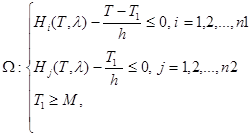
Функция двух переменных задана в замкнутой области 
. При условии, что область допустимых значений непустая, найдем решение ЗМП.
Критические точки являются решением системы:
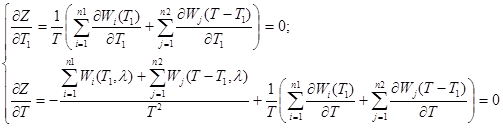
1. Учтем, что 
. Кроме того, 
– возрастает, а следовательно –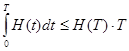
. Преобразуем частную производную 
:
Функция – возрастающая, тогда 
возрастает по переменной 
, а 
убывает по переменной . Следовательно, 
монотонно возрастает по . Тогда при фиксированном значении 
уравнение
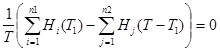(6)
имеет единственное решение.
2. Оценим значение частной производной 
:
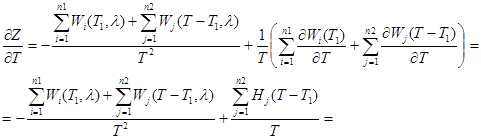
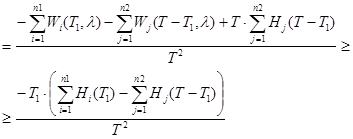
С учетом (6):
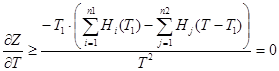(7)
То есть 
при всех значениях переменных и , если выполнено условие (6). Причем равенство нулю возможно только в случае, когда все неравенства:
;
обращаются в равенство, что возможно только в случае регулярного (
), а не случайного процесса. Следовательно, экстремума во внутренних точках области определения нет.
Ч.Т.Д.
Таким образом, алгоритм решения ЗМП (1-5):
1) проверяем, что область допустимых значений непустая;
2) исследуем на каждой из границ функцию 
; для этого решаем уравнение 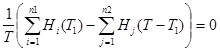, выразив через из уравнения границы;
3) среди всех найденных значений функции выбираем наименьшее.
Алгоритм численного решения задачи оптимизации параметров регулирования в узловой точке
Определим начальную точку для решения задачи (1)-(5) численным методом.
1-й этап. Считая 
, определим начальную точку для решения задачи (*) численным методом.
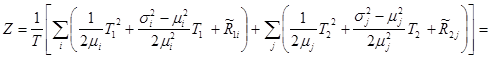
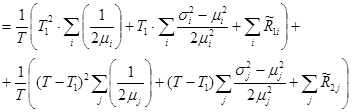
Здесь имеет место обозначение: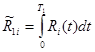 
, 
.
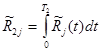Найдем производную по переменной :
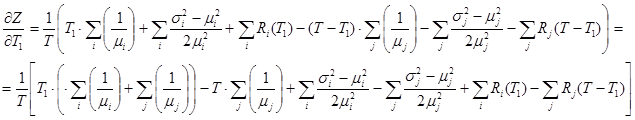
Причем, сумма интенсивностей всех потоков требований в узловой точке равна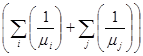 
, а сумма интенсивностей потоков на магистрали № 2 - 
.
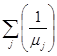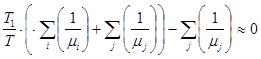
Пусть 
. При численном решении задачи можно взять в качестве начальной точки значение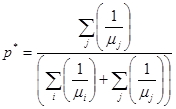 
.
2-й этап. Пусть , тогда 
, где 
, Т – переменная.
Найдем производную по переменной Т:
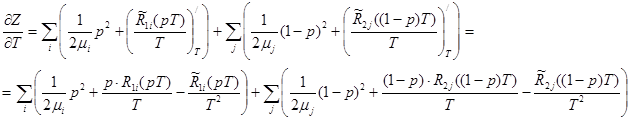
3-й этап. Для численного решения задачи математического программирования найдем начальную точку, принадлежащую области определения :
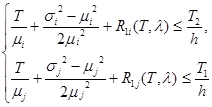
В качестве начальной точки можно взять значение:
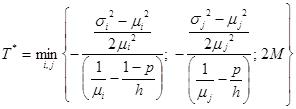
Алгоритм численного решения ЗМП:
1-й шаг. Задаем начальные значения:
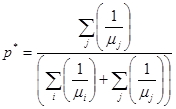и ;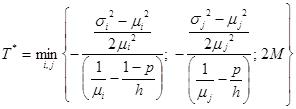
и значения для завершения алгоритма 
; 
; 
.
2-й шаг. Находим численно (например, методом половинного деления) решение 
уравнения 
, соответствующего условию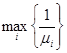 
;
3-й шаг. Проверяем выполнение остальных неравенств системы ограничений:
, ;
, ,.
4-й шаг. Если условия шага 3 выполнены, вычисляем 
и переходим к шагу 5. Если условия шага 3 не выполнены, то находим численно (например, методом половинного деления) решение уравнения 
, соответствующего условию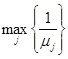 
. Проверяем выполнение остальных неравенств системы ограничений. Затем вычисляем и переходим к шагу 5.
5-й шаг. Приняв 
(начальное значение 
) находим численно решение 
уравнения:
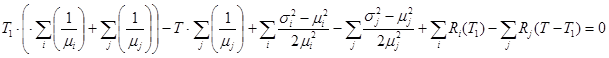
Тогда новое значение 
.
6-й шаг. Повторяем шаги 2-4 до тех пор пока 
.
Заключение
В работе приведен разработанный авторами алгоритм, который позволяет достаточно точно определять параметры светофорного регулирования в узловой точке транспортной сети по известному распределению интенсивностей по полосам движения. По результатам этих исследований разработана компьютерная программа в среде DELPHI. Данная работа является продолжением исследований авторов в этой области [5, 6]. В связи с тем, что математическая модель построена на гипотезе о распределении интервалов по времени по обобщенному закону Эрланга, результаты расчетов дают более точные результаты.
Работа выполнена при поддержке РФФИ, проект р-юг-а-13-08-96502.
Рецензенты:
Атрощенко В. А., д.т.н., профессор, декан Факультета компьютерных технологий ФГБОУ ВПО «Кубанский государственный технологический университет» Министерства образования и науки РФ, г.Краснодар.
Видовский Л. А., д.т.н., профессор, заведующий кафедрой Вычислительной техники и автоматизированных систем управления ФГБОУ ВПО «Кубанский государственный технологический университет» Министерства образования и науки РФ, г. Краснодар.