Введение
Потенциальная яма – это математический прием, который позволяет ограничить движение частиц плазмы в электромагнитном поле. Известно, что это такая ограниченная область пространства, в которой потенциальная энергия частицы меньше, чем вне ее, и энергия такой частицы может принимать лишь определенные дискретные значения. Разработаем модель потенциальной ямы на примере коаксиального магнитоплазменного ускорителя, который является электроэрозийным ускорителем. Исследование процесса электроэрозийного износа поверхности ускорительного канала с целью изучения характера износа по длине ствола, оптимизации электроэрозийной наработки рабочего материала и конструкции ускорителя является актуальной практической задачей.
Теоретический анализ
Приведем экспериментальные данные работы [6; 7] по измерению скорости в зависимости от координаты v(x), рис. 1а. Рядом приведен график скорости v(x), представленной в виде сплайновой функции, позволяющей производить аналитические операции над функцией скорости v(x), рис. 1б.
Предварительно преобразуем зависимость от координаты v(x) в зависимость от времени v(t) с помощью соотношений:
- ускорение определяется выражением
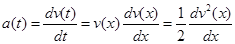 ;
; - время –
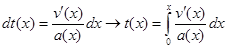 .
.
После подстановки зависимостей v(x) и a(x) в интегральные и дифференциальные соотношения получаем аналитические зависимости t(x) и x(t).
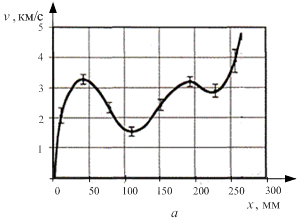
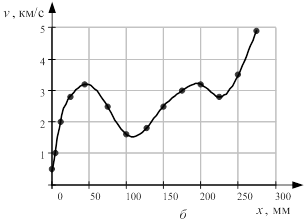
Рис. 1.Зависимость скорости v(x): а) экспериментальная; б) сплайновая
Таким образом, полученная зависимость скорости от времени имеет колебательный характер, рис. 2. Следовательно, для адекватности моделирования динамики распространения плазменного сгустка необходимо учитывать изменение массы сгустка в процессе его распространения [1; 2; 5; 6]. Колебательный характер скорости можно объяснить, рассматривая динамику распространения заряженных частиц в электромагнитном поле.
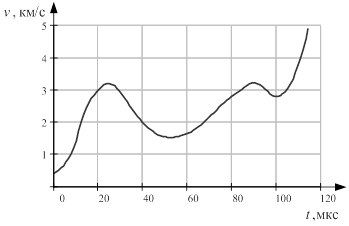
Рис. 2.Зависимость скорости плазменного сгустка от времени v(t)
Методика исследования
Магнитное поле плазменного укорителя можно представить как суперпозицию независимых ортогональных полей, создаваемых плазменным шнуром HПл=Hφ(r) (аксиальное поле) и индуктором HИнд={Hγ(z,r), Hz(z,r)} [2; 3; 6].
Поскольку нас интересует поле в области, ограниченной электродным стволом, то поле индуктора в этой области можно считать однородным, не зависящим от координат и имеющим только z-компоненту Hz=const. Напомним, что линии равного векторного потенциала Aэто силовые линии магнитного поля. Кроме магнитных полей, имеется и электрическое поле электродной системы «ствол-жгут», определяемое выражениями:
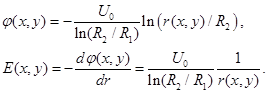
где φ(x,y) – потенциал электрического поля; U0 – напряжение, равное 3 кВ; R2, R1 – радиусы электрода ствола и плазменного жгута соответственно; E(x,y) – напряженность электрического поля.
Компоненты напряженности электрического поля E(x,y) по осям xи yбудут соответственно:
![]() . (1)
. (1)
Моделирование потенциальной ямы
Для ограничения траектории движения частиц в пределах ствола введена потенциальная функция U(x,y) – «потенциальная яма», имеющая аналитический вид:
![]() , (2)
, (2)
и ее силовая функция, которая определяется выражением, используя (1) и (2):
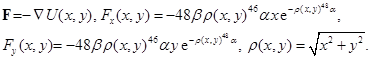
Входящие безразмерные коэффициенты имеют значения: β=104, α=10–60.
Экспериментальная часть
Пространственный вид потенциальной функции и силового поля представлены на рис. 3. На данном рисунке представлена локализация силы F(x,y)=–![]() U(x,y).
U(x,y).
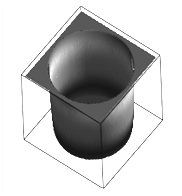
Рис. 3. Пространственное распределение потенциальной ямы U(x,y) и силовое поле F(x,y)=–![]() U(x,y)
U(x,y)
На основе полученных соотношений запишем уравнение динамики заряженных частиц в электромагнитных полях в векторной форме [4]:
![]() ,
, 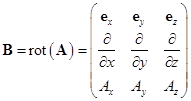 .
.
Систему дифференциальных уравнений второго порядка запишем в виде системы дифференциальных уравнений первого порядка в развернутом виде для каждой компоненты координаты и скорости:
![]()
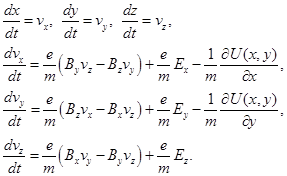
Решение дифференциальных уравнений осуществлялось методом Рунге–Кутта с фиксированным шагом с числом дискретизации N=103. Результаты расчетов приведены ниже. Все частицы имели одинаковую массу, заряд (+) и продольную компоненту скорости. Начальные значения поперечных скоростей и исходных координат частиц задавались различные. Относительные значения поперечных скоростей и координаты по отношению к радиусу электрода приведены на рис. 4. Видно, что при больших поперечных скоростях получаются большие радиусы. При заданной конфигурации электромагнитного поля частицы движутся по спирали.
а  б
б 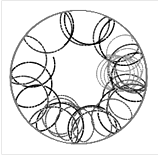 в
в 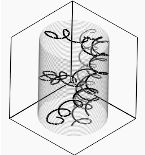
Рис. 4.Результаты расчета уравнения динамики заряженных частиц в электромагнитных полях: а) начальные положения координат и поперечные величины и направления скоростей; б) проекция траектории частиц на плоскость x, y; в) вид пространственной траектории частиц
Траектория, усредненная по ларморовскому периоду, тоже представляет собой спираль более низкой частоты. Таким образом, при распространении частиц центр окружности, по которой вращаются частицы в поперечной плоскости, движется по низкочастотной спирали. Соприкасаясь со стенками, частицы вызывают эрозию, в результате которой изменяется масса плазмы. Плазменный сгусток представлен в виде плазменного шнура [7]. Таким образом, масса пучка меняется по колебательному закону (рис. 5).
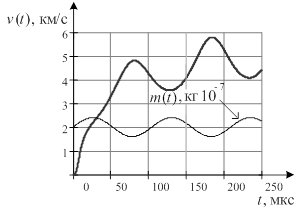
Рис. 5. Скорость сгустка с учетом эрозии при значениях параметров цепи C=12·10–3 Ф, L0=1,722·10–7 Гн, L′=4,6·10–7 Гн, U0=3 кВ
С учетом этого обстоятельства перепишем систему уравнений равновесия напряжения, тока и динамики сгустка:
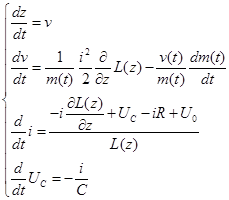 .
.
В качестве модели изменения массы m(t) выберем функцию:
m(t)= m0(1+ξsin(ωt)),
где m0=10–7 кг, ξ=0,2, ω=6·105.
Рассматривая зависимость скорости от времени (рис. 5), видим, что полученный результат находится в удовлетворительном согласии с экспериментальными данными. Заметим, что изменения массы и изменения скорости находятся в противофазах.
В балансе энергии добавляется эффективная потенциальная энергия, обусловленная изменением массы и равная величине [7]:
UЭф![]() .
.
Отсюда баланс энергии записывается в виде:
![]() .
.
Графическое представление баланса энергии приведено на рис. 6.
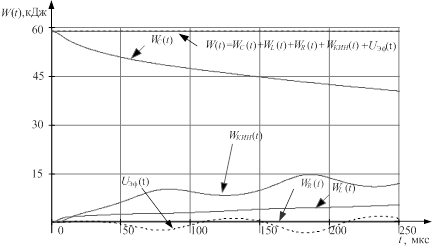
Рис. 6. Баланс энергии
Ниже приводится таблица сравнения экспериментальных и расчетных данных (табл. 1).
Таблица 1.Сравнение экспериментальных и расчетных данных
|
Величина |
Эксперимент |
Теория |
|
Индуктивность, L0, Гн |
(2…6)·10–7 |
1,72·10–7 |
|
Скорость, v, м/с |
4…10 |
6 |
|
Ток, I, кА |
80…120 |
90 |
|
Пространственная длительность процесса, x, мм |
240 |
250 |
|
Ускорение, a, км/с2 |
2·105 |
1,8·105 |
Таким образом, разработанная модель потенциальной ямы на примере коаксиального магнитоплазменного ускорителя позволяет наглядно проследить за движением частиц по низкочастотной спирали.
Низкочастотное спиральное движение есть суперпозиция движений:
· поперечного, обусловленного вращением частиц в поперечном направлении к магнитному полю и ограниченного потенциальным барьером, моделирующим поперечные размеры цилиндра;
· продольного – движение частиц вдоль оси цилиндра, параллельно магнитному полю. Это движение обусловлено магнитным давлением, толкающим плазменную субстанцию к выходу цилиндра. Соприкасаясь со стенками, частицы вызывают эрозию цилиндра и изменение массы плазмы.
Результаты
Предложен вид потенциальной ямы и силового поля, моделирующих пространственное ограничение разлета частиц плазмы. Установлены общие закономерности электроэрозийного износа поверхности ускорительного канала коаксиального магнитоплазменного ускорителя, которые определяются как энергетическими характеристиками, так и газодинамическими закономерностями гиперзвуковых струйных течений в цилиндрическом канале. Рассчитан баланс энергии с учетом эрозии.
Приведена таблица сравнения экспериментальных и теоретических данных, свидетельствующая в пользу удовлетворительной работы предложенной математической модели.
Работа выполнена в рамках государственного задания «Наука» 7.2826.2011 «Разработка и создание гибридной модели энергоблоков электростанций».
Рецензенты:
Лукутин Б.В., д.т.н., заведующий кафедрой ЭПП ЭНИН ФГБОУ ВПО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск.
Курец В.И., д.т.н., профессор кафедры ЭСиЭ ЭНИН ФГБОУ ВПО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск.



