Проблема разработки методик аналитико-экспертного оценивания для описания динамических характеристик объектов весьма актуальна для лиц, анализирующих поведение сложных систем, информация о свойствах которых представляется не только в числовой форме, но и в виде неформализованных знаний, выраженных в экспертных суждениях. Кроме того, существующие методы не учитывают влияние фактора времени в процессе анализа и оценки поведения объектов, что ограничивает описание динамических систем и не всегда может гарантировать достоверность получаемых результатов в процессе принятия решений на определенный момент времени. Преодоление указанных ограничений решается путем применения концепции динамических нечетких множеств [4,5].
Даже при отсутствие точных данных о значениях каких – либо критериев, лицо, принимающее решение или эксперт в состоянии описать их словами, например, «в последние несколько лет наши конкурентные преимущества достаточно высоки», «на протяжении текущего года сохраняется высокий уровень спроса» и т.д. Такой оценки вполне достаточно для определения функций принадлежности лингвистических переменных и их компьютерной обработки наряду с другими, более детерминированными показателями. Множество значений лингвистической переменной составляют нечеткие множества, смысловое значение которых заключается в том, что они характеризует определенный оценочный уровень или класс, такой как, например, «низкий-средний-высокий». В общем случае для оценки состояния объекта на основе знаний эксперта требуется построить динамические нечеткие множества для каждого параметра исследуемого объекта, произвести математические вычисления и определить к какому кластеру принадлежит значение исследуемого показателя.
Исходным пунктом для построения ДНМ является постановка задачи предметной области 
, так как именно особенности изучаемого предмета задают основные характеристики для моделирования, отражают смысловую нагрузку решаемой задачи, служат базой для определения критериев оценки и ограничений задачи.
,
где
– набор критериев для принятия решения;
- набор лингвистических переменных;
- область определения лингвистических переменных;
- горизонт построения модели;
- реперные точки и точки бифуркации.
В результате обработки исходных данных и применения вычислительных экспериментом, получаем динамические терм-множества значений критериев
.
Описание нечетких подмножеств осуществляется путем формирования соответствующих динамических функций принадлежности в следующей последовательности:
- Указание реперных и бифуркационных точек на всем горизонте построения модели[4];
- Формирование массивов экспериментальных данных из указанных экспертом точек, описывающих степень принадлежности каждого исследуемого параметра заданному нечеткому множеству в разные моменты времени[3];
- Поиск неизвестных точек путем применения алгоритмов аппроксимации[5];
- Описание динамических нечетких множеств и их графическое представление в виде построения динамических функций принадлежности;
- Построение динамического терм-множества значений показателей.
Алгоритмизация процесса построения динамических нечетких множеств, в том числе описание взаимодействия элементов и информационных потоков, представлена функциональной моделью на рисунке 1. На входе диаграммы – постановка задачи, на выходе – динамические терм-множества значений критериев. Эксперт снабжает систему знаниями об исследуемом объекте предметной области, реперными и бифуркационными точками на всем горизонте построения модели, подбирает вид функций принадлежности в разные периоды времени [6]. Для работы системы необходимо формирование базы данных и базы знаний.
После формулировки задачи предметной области и определения исследуемого объекта, формируется база данных, которая будет включать в себя множество параметров для оценки объекта, которые могут объединяться в группы по классификационным признакам, и множество лингвистических переменных, значения которых характеризуют выбранные параметры по подмножествам. База критериев и база показателей формируют те признаки, факторы или атрибуты, по которым производится оценка интегрального показателя. Базы знаний содержат информацию относительно формирования области определения лингвистических переменных для каждого параметра во все промежутки времени.
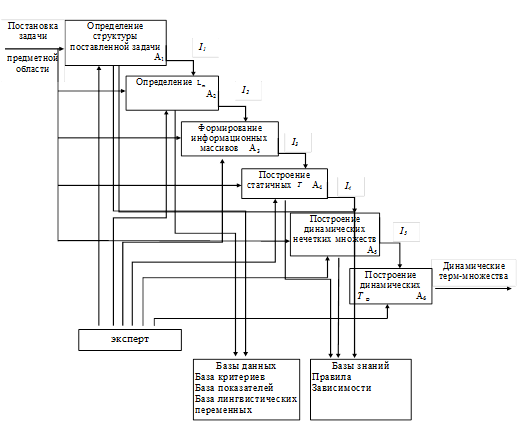
Рис. 1. Функциональная модель процесса построения динамических функций принадлежности
Информационный поток процесса моделирования динамических функций принадлежности показателей качества жизни населения региона представляется следующим образом:
In = {I1, I2, I3, I4, I5, I6},
где I1 – данные о выбранных критериях и показателях оценки интегрального показателя и количестве временных срезов; I2 – данные о лингвистических переменных для описания состояния показателей качества жизни населения; I3 – множество данных для формирования информационных массивов экспертных данных; I4 - множество данных для построения статических терм-множеств значений показателей качества жизни населения; I5 - множество данных для построения динамических нечетких множеств показателей качества жизни населения; I6 - множество данных для построения динамических терм-множеств значений показателей качества жизни населения.
На основе теоретических и прикладных исследований было разработано программное средство динамического нечеткого моделирования интерактивного процесса экспертного оценивания свойств сложных систем, визуализированных с помощью трехмерных графиков. Данная информационная система предполагает решение следующих функциональных задач:
- Редактирование и ввод данных;
- Построение двумерной функции принадлежности для определенного момента времени;
- Аппроксимацию недостающих значений;
- Построение динамических функций принадлежности.
Информационную систему решено было разработать в интегрированной среде разработки Lazarus на языке Object Pascal. Основные этапы работы программы представлены на рис. 2.
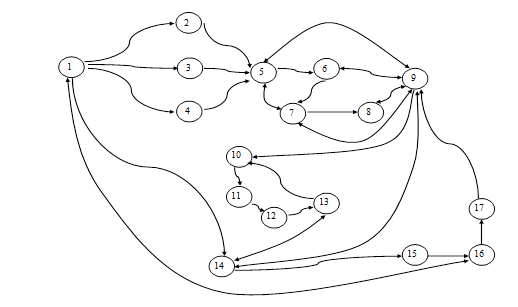
Рис.2. Граф работы информационной системы
1 – Запуск; 2 – Новая задача; 3 – Открыть задачу; 4 – Открыть задачу из списка последних файлов; 5 – Ввод частных показателей оценивания; 6 – Ввод исходных данных о лингвистических переменных, определяющих кластеры; 7 – Установка интервала времени; 8 - Сохранение задачи в файл; 9 – Редактирование исходных данных; 10 – Определение законов построения функций принадлежности нечетким множествам; 11- Определение величины и границы зоны абсолютной уверенности; 12 – Определение реперных и бифуркационных точек; 13 – Подбор функциональной зависимости и определение типа статической функции принадлежности; 14 – Построение 2D модели нечеткого множества; 15 - Аппроксимация недостающих значений по периодам для моделирования ДНМ; 16 - 3D визуализация ДНМ; 17 – Завершение работы.
Процесс внесения исходных данных автоматизирован следующим образом: эксперту предоставляется экранная форма (рис.3, а), куда необходимо занести исходные данные о нечетком множестве, наименовании и количестве оценочных уровней (кластеров), указать число временных периодов. Внесенные сведения автоматически переносятся на следующую экранную форму (рис.3,б). Для удобства восприятия пользователем, экранная форма работающей программы разбита на два блока: исходных данных и графического представления, причем правый график иллюстрирует статические функции принадлежности, а на левом отражается динамическое нечеткое множество после аппроксимации недостающих значений. По мере внесения информации по элементам, на графике слева появляются точки и строится кривая (рис. 3, б). Построение динамических нечетких множеств осуществляется отдельно для каждого оценочного уровня. Эксперт выбирает в окне программы показатель, временной период и вносит данные о виде функций принадлежности для каждого уровня, указывает известные ему реперные и бифуркационные точки. Нажатие на кнопку «Аппроксимация» запускает автоматизированный процесс поиска недостающих значений функции принадлежности, после чего появляется график динамического нечеткого множества (рис. 3,в).
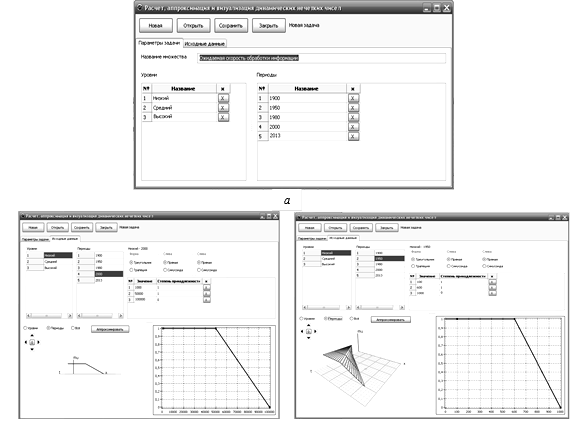
Рис.3 . Экранные формы автоматизированной системы моделирования динамических нечетких множеств
Разработанный математический аппарат и его программная реализация не ограничивают эксперта в выборе предметной области, числе исследуемых показателей и горизонте планирования. Множество элементарных операций, из которых состоит процесс построения динамических нечетких множеств, легко алгоритмизируются и реализуются с помощью вычислительных машин (рис. 3).
Рецензенты:
Рогачев А.Ф., д.т.н., профессор, заведующий кафедрой «Математическое моделирование и информатика», Волгоградский государственный аграрный университет, г. Волгоград.
Терелянский П.В., д.э.н., доцент, заведующий кафедрой «Информационные системы в экономике», Волгоградский государственный технический университет, г. Волгоград.