Введение
Важнейшим звеном информационных технологий является технология управления. Во многих случаях технологические процессы (объекты) могут быть отнесены к классу линейных. В этой связи актуальной остается проблема разработки алгоритмов регулирования и управления динамическими процессами. На практике для регулирования подобных процессов используются П-, ПИ-законы регулирования и т.п. Основная задача в этом случае сводится к настройке параметров соответствующих регуляторов, обеспечивающих удовлетворительное качество. Большинство используемых законов регулирования сопряжены с естественными потерями, связанными с проблемой настройки параметров. Причем, эти потери будут тем более значительными, чем более высок порядок уравнения, описывающего процесс. Технически типовые законы регулирования реализуются в настоящее время с использованием регулирующих приборов. Для настройки параметров регуляторов может быть использована непараметрическая модель ЛДС. При этом настройка осуществляется в процессе оптимизации сформированного критерия среднеквадратического отклонения выхода непараметрической модели и соответствующей аппроксимации оператора объекта регулирования.
В рамках современной теории управления линейными процессами разработаны методы оптимального и дуального управления. Для применения этих методов необходимо обладать исчерпывающими знаниями об объекте управления. На практике исследователь сталкивается с неполнотой априорной информации, влиянием случайных помех. В этих условиях необходима разработка новых методов и реализующих их алгоритмов управления, учитывающих неполноту информации об объекте управления[1,6]. Непараметрический подход к синтезу регулятора позволяет справиться с указанными проблемами.
Аналоговые средства локальной автоматики являются в достаточной степени надежными, и удовлетворительно справляются с задачами регулирования. Разработка более качественной системы регулирования предполагает использование современной цифровой техники. Учитывая возможность сбоя цифровых управляющих устройств компьютеров целесообразно сохранить аналоговые средства, тем более что опыт их использования и настройки регуляторов достаточно велик.
Целью работы является разработка двухконтурной системы регулирования, внедрение которой подразумевает использование установленной ранее автоматики, а также алгоритм настройки типовых регуляторов с использованием непараметрической модели.
Двухконтурная схема
Схема двухконтурного управления представлена на рис. 1. На рисунке приняты следующие обозначения: u(t) и x(t) соответственно входные и выходные параметры; ![]() – задающее воздействие для аналогового регулятора, которое вырабатывает непараметрический регулятор; x*(t) – задающее воздействие для непараметрического регулятора;
– задающее воздействие для аналогового регулятора, которое вырабатывает непараметрический регулятор; x*(t) – задающее воздействие для непараметрического регулятора; ![]() ,
, ![]() – помехи в каналах измерения.
– помехи в каналах измерения.
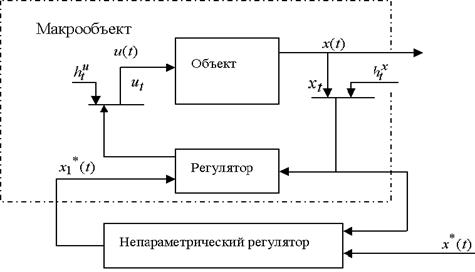
Рис.1. Схема двухконтурного управления
Опишем, что представляют собой два контура управления. Первым контуром регулирования является объект с аналоговым регулятором, второй контур – цифровой. Первый контур представляет собой объект регулирования для второго контура, то есть макрообъект.
Требуется построить непараметрический регулятор макрообъекта по входным-выходным параметрам ![]() и x(t), которые снимаются с макрообъекта в дискретные моменты времени Dt, предполагаем, что в каналах связи действуют помехи
и x(t), которые снимаются с макрообъекта в дискретные моменты времени Dt, предполагаем, что в каналах связи действуют помехи ![]() с нулевым средним и ограниченной дисперсией. Процесс построения регулятора разбивается на два этапа. Первый этап – построение непараметрической модели макрообъекта, второй этап – синтез непараметрического регулятора.
с нулевым средним и ограниченной дисперсией. Процесс построения регулятора разбивается на два этапа. Первый этап – построение непараметрической модели макрообъекта, второй этап – синтез непараметрического регулятора.
Сущность предлагаемого метода построения модели макрообъекта состоит в следующем. Известно, что реакция линейного динамического объекта описывается интегралом Дюамеля при нулевых начальных условиях:
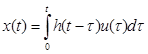
где h(t) весовая (импульсная переходная) функции системы.
В рассматриваемом случае, когда в качестве объекта берется не только объект управления, но и аналоговый регулятор, то интеграл свертки запишется в виде:
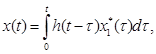
где h(t) будут уже соответственно переходная и весовая функции макрообъекта. Такая запись справедлива, поскольку и объект, и регулятор линейны. Тогда задача сводится к оцениванию весовой функции макрообъекта на основе имеющихся измерений.
Как известно, весовая функция h(t) является первой производной по времени от переходной характеристики. Учитывая этот факт необходимо на основе выборки (k1, t1), …, (ks, ts) получить оценку переходного процесса:
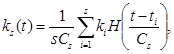
где s – объем выборки, H(×) – колоколообразная (ядерная) функция, Сs - параметр размытости, которые удовлетворяют условиям сходимости [2]. Оценка весовой функции примет вид:
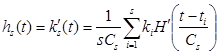 .
.
Подставив оценку весовой функции в интеграл свертки, получим непараметрическую модель макрообъекта:
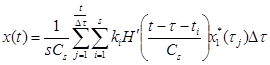 .
.
Параметр размытости Cs выбирается из минимума среднеквадратичного критерия[4]:
![]()
Второй этап построения непараметрического регулятора макрообъекта сводится к оценке обратной весовой характеристики системы. Известно, что обратный оператор линейной динамической системы (ЛДС) имеет тот же вид, что и прямой оператор ЛДС, с той лишь разницей, что весовая и переходная функции определяются в направлении «выход-вход» [3]. Поскольку на реальном объекте такие реализации получить нельзя, обратные характеристики снимаются с модели ЛДС, решая уравнение xs(t) = 1(t) для входа макрообъекта ![]() . Решение данного уравнения – есть алгоритм для вычисления точек обратной переходной функции w[t] и выглядит следующим образом:
. Решение данного уравнения – есть алгоритм для вычисления точек обратной переходной функции w[t] и выглядит следующим образом:
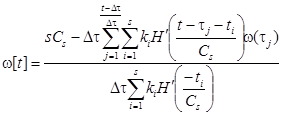 , где w[0]=0.
, где w[0]=0.
Полученная реализация ![]() используется для построения обратного оператора макрообъекта, оценка которого приведена ниже:
используется для построения обратного оператора макрообъекта, оценка которого приведена ниже:
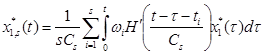 ,
,
где ![]() оценка обратного оператора макрообъекта, wi – реализация обратной переходной функции макрообъекта, x*(t) – задающее воздействие для макрообъекта, функция H(×) и параметр размытости Cs удовлетворяют тем же условиям сходимости [2].
оценка обратного оператора макрообъекта, wi – реализация обратной переходной функции макрообъекта, x*(t) – задающее воздействие для макрообъекта, функция H(×) и параметр размытости Cs удовлетворяют тем же условиям сходимости [2].
Особенностью построения модели макрообъекта является то факт, что переходная характеристика снимается с объекта, замкнутого аналоговым контуром регулирования. Таким образом, единичное ступенчатое воздействие 1(t) является заданием для аналогового регулятора, а не входным воздействием для объекта. Далее при построении второго контура регулирования – непараметрический регулятор вырабатывает управляющее воздействие ![]() для макрообъекта, которое в свою очередь является заданием для аналогового регулятора.
для макрообъекта, которое в свою очередь является заданием для аналогового регулятора.
Настройка параметров типовых регуляторов с использованием непараметрической модели линейной динамической системы
На рис. 2 изображена схема системы регулирования. Здесь x*(t) – заданное значение регулируемой величины, x(t) – регулируемая величина, u(t) – регулирующее воздействие, m(t) – возмущающее воздействие, W(p) и Wp(p) – соответственно операторы линейной системы и регулятора.
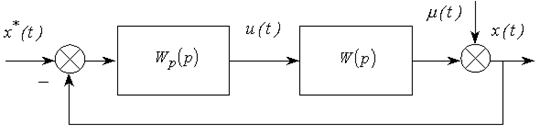
Рис. 2. Схема системы регулирования
Кратко опишем принципы построения типовых регуляторов. Опыт показывает, что переходные характеристики подавляющего большинства встречающихся на практике промышленных объектов регулирования обычно достаточно хорошо аппроксимируются динамической (инерционной) системой 2-го порядка с запаздыванием. Такая система описывается дифференциальным уравнением.
![]() .
.
В операторной форме описание системы имеет вид
![]() ,
,
где ![]() – коэффициент передачи объекта регулирования, t - постоянная чистого запаздывания.
– коэффициент передачи объекта регулирования, t - постоянная чистого запаздывания.
В тех случаях, когда может быть допущена большая динамическая ошибка регулирования, возможна аппроксимация объекта регулирования динамической системой 1-го порядка с запаздыванием (в этом случае T2 = 0) или даже просто безынерционной системой с запаздыванием (T2 = T1 = 0).
Приближенная передаточная функция оптимального регулятора может быть представлена в следующем виде
![]() ,
,
где Wo(p) – передаточная функция объекта регулирования без учета запаздывания. В результате передаточные функции описанных выше регуляторов будут следующими
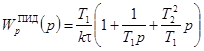 ,
, 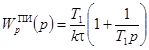 ,
, ![]() .
.
Такие регуляторы называются типовыми и осуществляют соответственно ПИД, ПИ и И законы регулирования.
Предложен следующий подход к настройке параметров регуляторов. Коэффициенты k и t могут быть определены экспериментально. Коэффициент передачи объекта регулирования k будет равен отношению значения выходной величины объекта к его входу в установившемся режиме работы. Постоянная запаздывания t также может быть определена опытным путем. Параметры T1 и T2 определяются в результате оптимизации следующего критерия[4]:
![]() (1)
(1)
где xs(t, u) – реакция непараметрической модели ЛДС на входное воздействие u(t), xa(T1, T2, t, u) – реакция аппроксимирующей параметрической модели ЛДС, соответствующей выбранному типовому регулятору, на аналогичное входное воздействие.
Для построения непараметрической модели ЛДС необходимо провести серию экспериментов напрямую с объектом регулирования. Однако на практике может возникнуть такой случай, когда невозможно разомкнуть существующую схему регулирования без ущерба для самого объекта. Тогда, имея информацию о типе и текущих параметрах существующего регулятора, определяем переходную функцию объекта. Описание идеи, которая при этом реализуется, приведено ниже. Пусть оператор замкнутой системы имеет вид
![]() ,
, ![]()
Применяя обратное преобразование Лапласа к обеим частям равенства, получаем интегральное уравнение
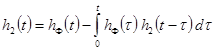 , (2)
, (2)
где ![]() ,
, ![]() ,
, ![]() – импульсные переходные функции звеньев схемы регулирования и замкнутой системы соответственно,
– импульсные переходные функции звеньев схемы регулирования и замкнутой системы соответственно,
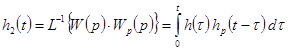 , (3)
, (3)
где hp(t) определяется типом и текущими настройками регулятора и предполагается известным, оценка hФ(t) также известна. Таким образом, заменяя импульсные переходные функции их непараметрическими оценками, последовательно отыскиваем численное решение интегральных уравнений: уравнения (2) относительно h2(t) на первом этапе и уравнения (3) относительно h(t) на втором этапе. В итоге получаем искомую оценку импульсной переходной функции объекта регулирования, которую и используем в вычислении критериальной функции (1). Вывод численного алгоритма решения задачи будет аналогичен выводу реализации переходной функции обратного оператора ЛДС
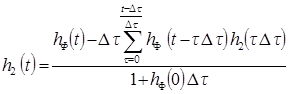 ,
, ![]() ,
,
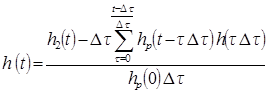 ,
, ![]() .
.
Важным вопросом, который возникает при решении задачи настройки параметров типовых регуляторов, является проблема синтеза устойчивой системы. При определении параметров настройки из условия минимума среднеквадратической ошибки регулирования потеря устойчивости как правило не наблюдается. Однако переходные процессы в такой системе часто имеют характер затухающих колебаний, интенсивность затухания которых, как правило, оказывается недостаточной. Поэтому в критерий оптимального функционирования системы регулирования приходится обычно вводить дополнительные ограничения, с помощью которых можно целенаправленно влиять на возникающие в ней переходные процессы.
Так оптимизация критериальной функции (2) по параметрам T1 и T2 проводится с учетом ограничений, определяемых из условий устойчивости. Для выделения области устойчивости можно воспользоваться, например, методом D-разбиения.
Заключение
В статье предлагается решение задачи синтеза двухконтурной схемы регулирования с использованием в качестве второго контура непараметрического регулятора линейных динамических систем. В основе предложенного алгоритма лежит непараметрическая модель динамики. Двухконтурная схема регулирования предполагает сохранение аналоговых средств локальной автоматики, что делает ее надежной при сбое цифрового контура управления. Приводится подробное описание алгоритмов настройки типовых аналоговых средств локальной автоматики с использованием непараметрической модели ЛДС.
Можно сделать вывод, что представленный подход позволяет эффективно решать вышеперечисленные задачи и может широко применяться при построении сложных систем управления технологическими процессами в энергетике и различных отраслях промышленности.
Рецензенты:
Бронов С.А., д.т.н., профессор, руководитель научно-учебной лаборатории систем автоматизированного проектирования кафедры систем искусственного интеллекта Сибирского федерального университета, г. Красноярск.
Ченцов С.В., д.т.н., профессор, зав. кафедрой «Системы автоматики, автоматизированного управления и проектирования» Сибирского федерального университета, г. Красноярск.



