Введение
На работоспособность технических средств и самочувствие человека оказывает влияние ряд факторов природного происхождения. Среди них особое внимание уделяется магнитному полю Земли (МПЗ). В периоды возмущения геомагнитной активности (ГМА) выявлено негативное влияния МПЗ как на самочувствие человека, так и на работоспособность технических средств [12]. У метеозависимых людей наблюдаются нарушения функционирования сердечно-сосудистой и нервной систем, повышается риск инсультов [6], наблюдаются сбои в работе систем навигации космических летательных объектов, трансформаторов, систем радиосвязи [8]. Современные методы прогноза геомагнитных возмущений, основанные на оптических наблюдениях за активностью Солнца и анализе процессов на его поверхности, обладают сложностью исполнения и невысокой достоверностью [5]. Поэтому проблема мониторинга и прогнозирования ГМА является в настоящее время весьма актуальной.
Цель работы: изучение и анализ модели АРПСС для прогнозирования геомагнитных возмущений.
Материал и методы исследования. Статистическая обработка материала и вычисления проводились с использованием пакета прикладных программ MSExcel 2003, statistica 6.0[12].
В качестве исходных данных использовались значения временных рядов вектора напряженности (ВН) геомагнитного поля(ГМП)H(t) с интервалом t=1 мин., за период 14 лет, измеренные на обсерватории ADDISABAB (AAE, Эфиопия), а также индексы геомагнитной активности K на каждый день из этого периода. С целью выявления возможности прогнозирования спокойного и возмущенного ГМП на первом этапе были выделены 10 рядов, не содержащих возмущений (невозмущенный ряд) H(НР)(t), т.е. приК-индекс![]() 4, и 10 рядов, содержащих магнитную бурю (возмущенный ряд)H(ВР)(t), т.е. при К-индекс>4.
4, и 10 рядов, содержащих магнитную бурю (возмущенный ряд)H(ВР)(t), т.е. при К-индекс>4.
Результаты и обсуждение
В ходе данной работы проводились исследования временных рядов значений ВНГМП для получения модели прогноза с использованием математического аппарата авторегрессии и проинтегрированного скользящего среднего (АРПСС). Данный метод чрезвычайно популярен во многих приложениях, и практика подтверждает его мощность и гибкость [11], он является наиболее распространенным общим методом стохастического моделирования во многих областях научных исследований и используется в тех случаях, когда нет отчетливо выраженных регулярных составляющих, а отдельные наблюдения содержат значительную ошибку.Метод АРПСС основан на использовании двух процессов [3]:
1) процесс авторегрессии, описывающий последовательную зависимость элементов временного ряда следующим уравнением [2]:
![]() ,
,
где ![]() - текущее значение временного ряда,
- текущее значение временного ряда, ![]() - константа (свободный член),
- константа (свободный член), ![]() ,
, ![]() ,
, ![]() ,... (-1<
,... (-1<![]() <1)- параметры авторегрессии,
<1)- параметры авторегрессии, ![]() - предшествующее значение временного ряда,
- предшествующее значение временного ряда, ![]() - случайная компонента. Данное уравнение показывает, что каждое наблюдение есть сумма случайной компоненты и линейной комбинации предыдущих наблюдений;
- случайная компонента. Данное уравнение показывает, что каждое наблюдение есть сумма случайной компоненты и линейной комбинации предыдущих наблюдений;
2) процесс скользящего среднего, описывающий суммарное воздействие предыдущих ошибок на каждый элемент ряда следующим уравнением:
![]() ,
,
где ![]() - свободный член скользящего среднего,
- свободный член скользящего среднего, ![]() ,
, ![]() ,
, ![]() , ... (-1<
, ... (-1<![]() <1) - параметры скользящего среднего,
<1) - параметры скользящего среднего, ![]() - случайная компонента. В общем виде модель записывается как АРПСС (p, d, q), где p – параметр авторегрессии, d – порядок разности, q – параметр скользящего среднего.Мультипликативная сезонная АРПСС представляет естественное развитие и обобщение обычной модели АРПСС на ряды, в которых имеется периодическая сезонная компонента. В дополнение к несезонным параметрам в модель вводятся сезонные параметры для определенного лага (устанавливаемого на этапе идентификации порядка модели). Аналогично параметрам простой модели АРПСС эти параметры называются: сезонная авторегрессия (Ps), сезонная разность (Ds) и сезонное скользящее среднее (Qs). Таким образом, полная сезонная АРПСС может быть записана как АРПСС (p,d,q)(Ps,Ds,Qs) [11]. Для построения модели использовался алгоритм, приведенный на рисунке 1, основанный на анализе автокорреляционной и частной автокорреляционной функций по правилам, приведенным ниже [2].
- случайная компонента. В общем виде модель записывается как АРПСС (p, d, q), где p – параметр авторегрессии, d – порядок разности, q – параметр скользящего среднего.Мультипликативная сезонная АРПСС представляет естественное развитие и обобщение обычной модели АРПСС на ряды, в которых имеется периодическая сезонная компонента. В дополнение к несезонным параметрам в модель вводятся сезонные параметры для определенного лага (устанавливаемого на этапе идентификации порядка модели). Аналогично параметрам простой модели АРПСС эти параметры называются: сезонная авторегрессия (Ps), сезонная разность (Ds) и сезонное скользящее среднее (Qs). Таким образом, полная сезонная АРПСС может быть записана как АРПСС (p,d,q)(Ps,Ds,Qs) [11]. Для построения модели использовался алгоритм, приведенный на рисунке 1, основанный на анализе автокорреляционной и частной автокорреляционной функций по правилам, приведенным ниже [2].
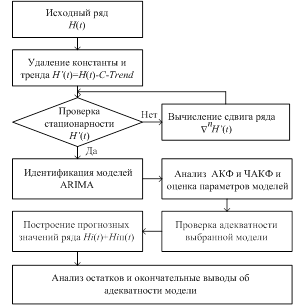
Рисунок 1 – Алгоритм получения модели АРПСС
- Один параметр (p): АКФ - экспоненциально затухает; ЧАКФ - имеет выброс для лага 1, для других значений задержек корреляции нет.
- Два параметра авторегрессии (p): АКФ имеет форму затухающей синусоиды или экспоненциально убывает; ЧАКФ имеет выброс на сдвигах 1 и 2, нет корреляций на других лагах.
- Один параметр скользящего среднего (q): АКФ имеет выброс на лаге 1, нет корреляций на других лагах; ЧАКФ экспоненциально убывает либо монотонно, либо меняя знак.
- Два параметра скользящего среднего (q): АКФ имеет выбросы на лагах 1 и 2, нет корреляций на других лагах. ЧАКФ имеет форму синусоиды или экспоненциально затухает.
- Один параметр авторегрессии (p) и один параметр скользящего среднего (q): АКФ экспоненциально убывает с лага 1; ЧАКФ - экспоненциально убывает с лага 1.
Исходные рядыH(НР)(t) и H(ВР)(t) подвергались математической обработке, в результате которой было удалено среднеезначение рядаC и тренд по формуле [9]:
![]() -
- 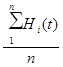 -
- ![]() ,
,
где 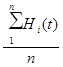 - среднее арифметическое ряда
- среднее арифметическое ряда ![]() , n – количество измерений,
, n – количество измерений, ![]() - линейный тренд.
- линейный тренд.
Для получения адекватной модели АРПСС необходимо, чтобы временной ряд имел стационарный характер [2], т.е. имел постоянные по времени среднееm = const, дисперсию σ2 = constи автокорреляции ![]() є (µ, σ2).
є (µ, σ2).
Проверить ряд на свойство стационарности можно, построив автокорреляционную (АКФ) и частную автокорреляционную функции (ЧАКФ) [3].Критерий нестационарности выражается в отсутствии тенденции к затуханию у выборочной автокорреляционной функции ряда H’(t) [11].Если это условие не выполняется, необходимо выполнить преобразование ряда ![]() к стационарному виду. Этого можно добиться с помощью операции нахождения разности ряда
к стационарному виду. Этого можно добиться с помощью операции нахождения разности ряда ![]() с лагом
с лагом ![]() по формуле:
по формуле:
![]() -
-![]() -
-![]() ,
,
где ![]() - значение ряда в данный момент времени,
- значение ряда в данный момент времени, ![]() -
-![]() - значение ряда в момент времени (t-
- значение ряда в момент времени (t-![]() ), n – количество операций взятия разности.
), n – количество операций взятия разности.
При достижении стационарности преобразованного ряда ![]() получаем параметр модели d=n [3]. На рисунке 2 представлены графики значений H’(НР)(t) и H’(ВР)(t) и их АКФ и ЧАКФ. На рисунках 2 в-е по вертикали отложены значения лага
получаем параметр модели d=n [3]. На рисунке 2 представлены графики значений H’(НР)(t) и H’(ВР)(t) и их АКФ и ЧАКФ. На рисунках 2 в-е по вертикали отложены значения лага ![]() , а по горизонтали коэффициенты корреляции K.
, а по горизонтали коэффициенты корреляции K.
а) 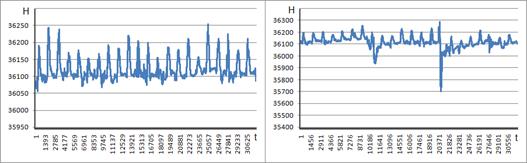 б)
б)
в)  г)
г)
д) 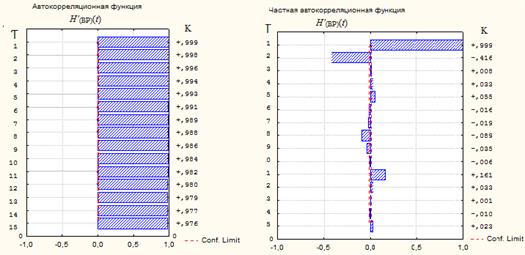 е)
е)
Рисунок 2–Временные ряды H’(НР)(t) (а) иH’(ВР)(t) (б) и их АКФ (в, д) и ЧАКФ (г,е) исходных значений
Из графиков видно, что анализируемые ряды имеют сильные корреляции (коэффициенты корреляции K на первых 15 лагах близки к 1), поэтому не являются стационарными [2].Применим разностный оператор ![]() сначала для лага
сначала для лага ![]() 1=1, а затем для лага
1=1, а затем для лага ![]() 2=1440 (так как априори известна периодическая составляющая солнечно-суточных вариаций ВН ГМП с периодом 24 часа), а взяв разность со значением лага, равным периоду сезонной компоненты временного ряда, можно исключить периодичную составляющую [11]. На рисунке 3 показаны АКФ и ЧАКФ полученных после применения разностного оператора
2=1440 (так как априори известна периодическая составляющая солнечно-суточных вариаций ВН ГМП с периодом 24 часа), а взяв разность со значением лага, равным периоду сезонной компоненты временного ряда, можно исключить периодичную составляющую [11]. На рисунке 3 показаны АКФ и ЧАКФ полученных после применения разностного оператора ![]() с лагами
с лагами ![]() 1=1 и
1=1 и ![]() 2=1440 рядов
2=1440 рядов ![]() 2H’(НР)(t) и
2H’(НР)(t) и ![]() 2H’(ВР)(t).
2H’(ВР)(t).
а) 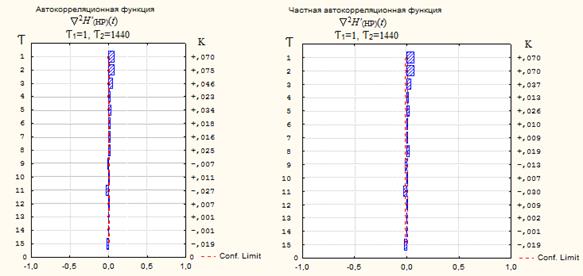 б)
б)
в) 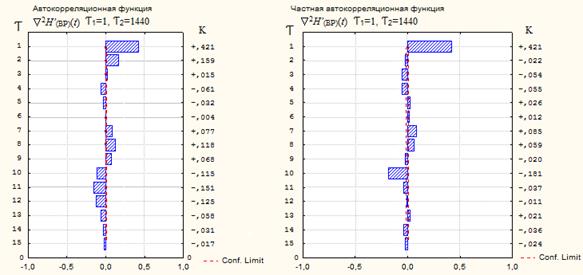 г)
г)
Рисунок 3 – АКФ и ЧАКФ полученных после взятия разностей с лагами ![]() 1=1 и
1=1 и
![]() 2=1440 рядов
2=1440 рядов ![]() 2H’(НР)(t) и
2H’(НР)(t) и ![]() 2H’(ВР)(t)
2H’(ВР)(t)
Из графиков АКФи ЧАКФ видно, что ряды ![]() 2H’(НР)(t) и
2H’(НР)(t) и ![]() 2H’(ВР)(t) имеют стационарный характер – нет периодичностей и ярко выраженных корреляционных пиков [4], что в соответствии с правилами [3] позволяет определить параметры моделикак (0,1,1)(1,1,0) с сезонным сдвигом 1440.О качестве применяемой модели можно судить лишь по совокупности сопоставлений прогнозных значений с фактическими. Простой мерой качества прогнозов является оправдываемость прогноза μ, что определяется формулой[9]:
2H’(ВР)(t) имеют стационарный характер – нет периодичностей и ярко выраженных корреляционных пиков [4], что в соответствии с правилами [3] позволяет определить параметры моделикак (0,1,1)(1,1,0) с сезонным сдвигом 1440.О качестве применяемой модели можно судить лишь по совокупности сопоставлений прогнозных значений с фактическими. Простой мерой качества прогнозов является оправдываемость прогноза μ, что определяется формулой[9]:
![]()
где p - количество подтвержденных фактическими данными прогнозов; q – количество неподтвержденных фактическими данными прогнозов. В таблице 1 приведены результаты оценки качества прогноза для каждого из десяти невозмущенных рядов Hn’(НР)(t) и каждого из десяти рядов Hn’(ВР)(t) для горизонта прогнозирования 1, 2 и 3 часа, где n– порядковый номер ряда.
Таблица 1 –Результаты оценивания параметров модели (0,1,1)(1,1,0)
|
Вид ГМП |
Ряд |
Параметр модели АРПСС |
Оценка параметра модели |
Нижняя граница 95% дов. интервала |
Верхняя граница 95% дов. интервала |
|
||||
|
1ч. |
2ч. |
3ч. |
||||||||
|
Невозмущенное поле |
H1’(НР)(t) |
q(1) |
-0,06 |
-0,07 |
-0,05 |
1,00 |
1,00 |
1,00 |
||
|
Ps(1) |
-0,51 |
-0,52 |
-0,50 |
|||||||
|
H2’(НР)(t) |
q(1) |
-0,37 |
-0,38 |
-0,36 |
1,00 |
1,00 |
1,00 |
|||
|
Ps(1) |
-0,52 |
-0,53 |
-0,51 |
|||||||
|
H3’(НР)(t) |
q(1) |
-0,26 |
-0,27 |
-0,25 |
1,00 |
1,00 |
1,00 |
|||
|
Ps(1) |
-0,49 |
-0,50 |
-0,48 |
|||||||
|
H4’(НР)(t) |
q(1) |
0,34 |
0,33 |
0,35 |
1,00 |
1,00 |
1,00 |
|||
|
Ps(1) |
0,49 |
0,50 |
0,48 |
|||||||
|
H5’(НР)(t) |
q(1) |
0,28 |
0,28 |
0,29 |
0,97 |
0,95 |
0,93 |
|||
|
Ps(1) |
0,16 |
0,15 |
0,17 |
|||||||
|
H6’(НР)(t) |
q(1) |
-0,08 |
-0,09 |
-0,07 |
0,94 |
0,92 |
0,90 |
|||
|
Ps(1) |
-0,51 |
-0,52 |
-0,50 |
|||||||
|
H7’(НР)(t) |
q(1) |
-0,27 |
-0,28 |
-0,29 |
0,98 |
0,96 |
0,94 |
|||
|
Ps(1) |
-0,39 |
-0,40 |
-0,38 |
|||||||
|
H8’(НР)(t) |
q(1) |
-0,08 |
-0,09 |
-0,07 |
1,00 |
1,00 |
1,00 |
|||
|
Ps(1) |
-0,51 |
-0,52 |
-0,50 |
|||||||
|
H9’(НР)(t) |
q(1) |
0,22 |
0,21 |
0,23 |
0,93 |
0,91 |
0,89 |
|||
|
Ps(1) |
-0,49 |
-0,50 |
-0,48 |
|||||||
|
H10’(НР)(t) |
q(1) |
-0,06 |
-0,07 |
-0,05 |
1,00 |
1,00 |
1,00 |
|||
|
Ps(1) |
-0,51 |
-0,52 |
-0,50 |
|||||||
|
Возмущенное поле |
H1’(ВР)(t) |
q(1) |
-0,11 |
-0,12 |
-0,10 |
0,34 |
0,33 |
0,32 |
||
|
Ps(1) |
-0,53 |
-0,54 |
-0,52 |
|||||||
|
H2’(ВР)(t) |
q(1) |
-0,34 |
-0,35 |
-0,33 |
0,15 |
0,15 |
0,15 |
|||
|
Ps(1) |
-0,47 |
-0,48 |
-0,46 |
|||||||
|
H3’(ВР)(t) |
q(1) |
-0,53 |
-0,52 |
-0,50 |
0,09 |
0,08 |
0,07 |
|||
|
Ps(1) |
-0,55 |
-0,56 |
-0,54 |
|||||||
|
H4’(ВР)(t) |
q(1) |
-0,46 |
-0,47 |
-0,45 |
0,22 |
0,21 |
0,20 |
|||
|
Ps(1) |
-0,50 |
-0,51 |
-0,49 |
|||||||
|
H5’(ВР)(t) |
q(1) |
-0,11 |
-0,12 |
-0,10 |
0,21 |
0,20 |
0,19 |
|||
|
Ps(1) |
-0,48 |
-0,49 |
-0,47 |
|||||||
|
H6’(ВР)(t) |
q(1) |
-0,14 |
-0,15 |
-0,13 |
0,05 |
0,05 |
0,04 |
|||
|
Ps(1) |
-0,53 |
-0,54 |
-0,52 |
|||||||
|
H7’(ВР)(t) |
q(1) |
-0,07 |
-0,08 |
-0,06 |
0,23 |
0,23 |
0,23 |
|||
|
Ps(1) |
-0,50 |
-0,51 |
-0,49 |
|||||||
|
H8’(ВР)(t) |
q(1) |
-0,07 |
-0,08 |
-0,06 |
0,25 |
0,24 |
0,23 |
|||
|
Ps(1) |
-0,51 |
-0,52 |
-0,50 |
|||||||
|
H9’(ВР)(t) |
q(1) |
-0,06 |
-0,07 |
-0,05 |
0,12 |
0,12 |
0,11 |
|||
|
Ps(1) |
-0,43 |
-0,44 |
-0,42 |
|||||||
|
H10’(ВР)(t) |
q(1) |
-0,08 |
-0,09 |
-0,07 |
0,29 |
0,29 |
0,28 |
|||
|
Ps(1) |
-0,51 |
-0,52 |
-0,50 |
|||||||
Из таблицы видно, что ![]() <0,4 для рядов H’(ВР)(t) и
<0,4 для рядов H’(ВР)(t) и ![]() > 0,8 для рядов H’(НР)(t). Это позволяет сделать вывод о том, что идентифицированная модель АРПСС (0,1,1)(1,1,0) не позволяет строить прогноз геомагнитных возмущений.
> 0,8 для рядов H’(НР)(t). Это позволяет сделать вывод о том, что идентифицированная модель АРПСС (0,1,1)(1,1,0) не позволяет строить прогноз геомагнитных возмущений.
На рисунке 4 представлены результаты прогноза временных рядов H1’(НР)(t) (а) иH1’(ВР)(t)(б) значений ВН ГМП с помощью модели АРПСС (0,1,1)(1,1,0).
а) 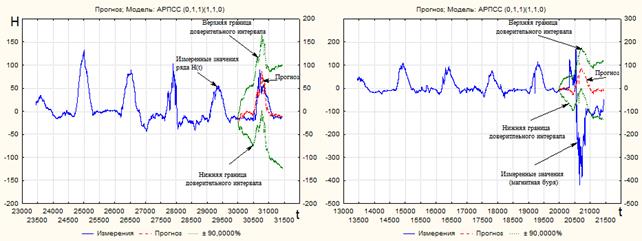 б)
б)
Рисунок 4 – Результаты прогноза с помощью АРПСС (0,1,1)(1,1,0) рядов H’(НР)(t) (а) иH’(ВР)(t) (б)
Из рисунка 4 видно, что модель адекватно строит прогноз для невозмущенного ряда H’(НР)(t), но не прогнозирует магнитную бурю в ряде H’(ВР)(t). Для проверки адекватности проанализируем временные ряды остатков HО’(НР)(t) и HО’(ВР)(t), АКФ которых приведены на рисунке 5.
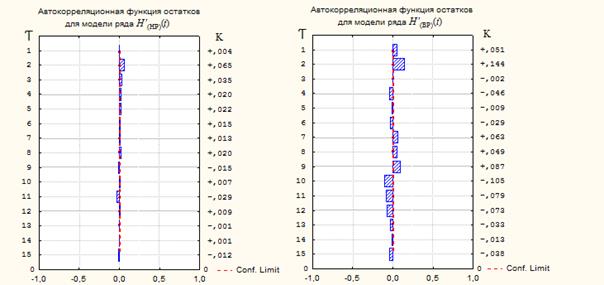
Рисунок 5–АКФ остатков для ряда H’(НР)(t) (а) и для ряда H’(ВР)(t) (б)
Из рисунка 5 видно, что остатки для H’(НР)(t) практически не имеют корреляций в то время, как остатки для H’(ВР)(t) имеют достаточно сильные корреляции.
Полученная модель АРПСС, не имеющая возможности прогнозирования возмущений ГМП (прогноз выходит за границы доверительного интервала), и анализ АКФ остатков позволяют сделать вывод о необходимости разработки нового более точного и эффективного метода прогнозагеомагнитных возмущений.
Таким образом, исследована возможность применения мультипликативной модели авторегрессии и проинтегрированного скользящего среднего, были выделены временные ряды, содержащие геомагнитную бурю, и невозмущенные значения вектора напряженности ГМП, из исходных рядов было удалено среднее значение Cи линейный тренд. С помощью применения разностного оператора ряды значений ВН ГМП приведены к стационарному виду и получена модель АРПСС для прогнозирования десяти рядов H’(НР)(t) и десяти рядовH’(ВР)(t); оценены параметры модели и построены прогнозы для каждого из них. Была проведена оценка адекватности прогноза и сделан вывод о неприменимости модели АРПСС для прогнозирования геомагнитных возмущений.
Результаты работы получены при поддержке Минобрнауки РФ в рамках государственного задания на проведение НИОКР, шифр заявки № 8.2935.2011
Рецензенты:
Кириевский Е.В., д.т.н., профессор кафедры «Информационные и измерительные системы и технологии» ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова», г.Новочеркасск.
Гречихин В.В., д.т.н., профессор кафедры «Информационные и измерительные системы и технологии», ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова», г.Новочеркасск.



