Введение
Цифровые фильтры применяются практически во всех областях техники, требующих обработки сигналов. Сюда относятся спектральный анализ, обработка изображений, видео, звук и др. Классический синтез цифровых фильтров заключается в получении описывающей его передаточной функции минимального порядка, соответствующей заданным характеристикам [3]. Это обусловлено тем, что при данном подходе фильтры реализуются аппаратно на базе R-L-C-элементов интегральных схем.
С появлением таких аппаратных платформ, как программируемые логические интегральные схемы (ПЛИС, FPGA), цифровые сигнальные процессоры (DSP) и системы на кристалле (SoC), стал осуществим новый подход, заключающийся в программной реализации цифровых фильтров. Данный тип синтеза позволяет улучшить точностные характеристики отфильтрованного сигнала за счет повышения порядка фильтра, однако имеет и свои недостатки: низкая скорость обработки сигнала, зависящая от быстродействия исполняющего процессора, сложность реализации цифровых фильтров высокого порядка, большие времена запаздывания сигнала, возрастающие с ростом порядка фильтра.
Современные программные пакеты моделирования, такие как MATLAB\Simulink и NI LabVIEW, позволяют синтезировать различные цифровые фильтры с желаемыми характеристиками и автоматически генерировать программный код под множество аппаратных платформ, список которых постоянно расширяется [4]. Таким образом, трудоемкость процесса проектирования устройств фильтрации значительно сокращается. Однако для увеличения точности обработки сигнала необходимо увеличивать порядок передаточной функции искомого цифрового фильтра, что приводит к росту времени обработки сигнала [5].
Представляется целесообразным распараллелить передаточную функцию фильтра, синтезируемого в инструментальном пакете моделирования, представив ее в виде суммы передаточных функций меньшего порядка. Такой подход позволит увеличить быстродействие устройств фильтрации без увеличения аппаратных затрат.
Описание решения
Поскольку любая передаточная функция является правильной рациональной дробью, то в соответствии со свойствами рациональных функций ее можно представить в виде суммы элементарных дробей (звеньев), что широко используется при аналитическом интегрировании.

, где B и A – многочлены с вещественными коэффициентами, причем степень B меньше степени A. Коэффициенты pi – вещественные или комплексные. Комплексные коэффициенты образуют сопряженные пары. Коэффициент ri – вещественная постоянная.
Поскольку реализация вычислительного алгоритма с использованием комплексных чисел затруднительна, необходимо привести звенья к виду, когда они не содержат комплексных коэффициентов. Перемножим звенья с комплексно-сопряженными коэффициентами pi, и получим передаточные функции вида:
![]()
, где li, ri, mi, pi – вещественные числа.
Таким образом, любую передаточную функцию можно представить в виде суммы отдельных передаточных функций, порядок которых не превышает второго (3). При этом все коэффициенты суммы являются вещественными числами, что важно при реализации передаточных функций на специализированных вычислителях.

, где Hi(s) – передаточная функция с вещественными коэффициентами либо первого порядка (1), либо второго порядка (2).
Для увеличения точности обработки сигнала часто прибегают к увеличению порядка описывающей фильтр передаточной функции, что приводит к росту времени обработки сигнала. При реализации фильтра в форме (3) рост порядка передаточной функции будет оказывать незначительное влияние на общее время вычислений при реализации на платформах, поддерживающих параллельные вычисления, таких как ПЛИС или многоядерные системы, поскольку каждое интегрирующее звено из общей суммы может вычисляться независимо от остальных. Таким образом, можно достичь выигрыша в точности вычислений за счет увеличения аппаратных затрат, при этом сохраняя общее время обработки сигнала практически неизменным.
Рассмотрим пример параллельной реализации эллиптического фильтра в среде LabVIEW с использованием функций MathScript. Наиболее распространенными способами математического описания фильтров в средах MATLAB и LabVIEW являются передаточная функция (Transfer Function, tf) и набор нулей полюсов и коэффициента передачи (Zero-Pole-Gain, zpk). Синтезируем искомый фильтр в обеих формах tf и zpk (4) и проанализируем результаты. На рисунке 1 показан фрагмент блок-диаграммы, реализующий синтез эллиптического фильтра в узле MathScript Node в виде передаточной функции и набора нулей полюсов и коэффициента передачи. Параметры синтезируемого эллиптического фильтра следующие:
- порядок передаточной функции – 9;
- величина пульсаций АЧХ в полосе пропускания – 0,001 дБ;
- подавление сигнала в полосе задерживания – 50 дБ;
- частота среза – 7,8 Гц;
- вид фильтра – фильтр нижних частот;
- тип передаточной функции – непрерывная (s-область);
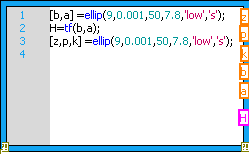
Рисунок 1. Фрагмент блок-диаграммы виртуального прибора, реализующий синтез эллиптического фильтра в узле MathScript Node в виде tf и zpk
Передаточная функция синтезированного фильтра (4).
![]()
![]()
На рисунке 2 показана амплитудно-частотная характеристика синтезированного эллиптического фильтра.
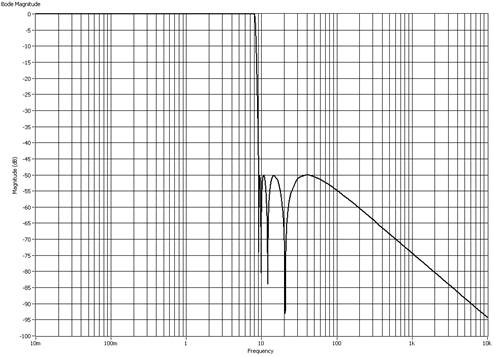
Рисунок 2. Амплитудно-частотная характеристика синтезированного эллиптического фильтра 9 порядка
Целесообразно автоматизировать процесс перехода от стандартного математического описания фильтра к описанию в форме (3). Для этого необходимо программно реализовать два алгоритма преобразования для каждой формы представления фильтра (tf и zpk). На рисунке 3(а) показан узел MathScript Node, содержащий текст программы для перехода от формы описания в виде tf к массиву передаточных функций первого и второго порядка, сумма которых эквивалентна исходной передаточной функции фильтра. На рисунке 3(б) показаны узлы MathScript Node с текстом скрипта перехода от zpk к аналогичному массиву передаточных функций.
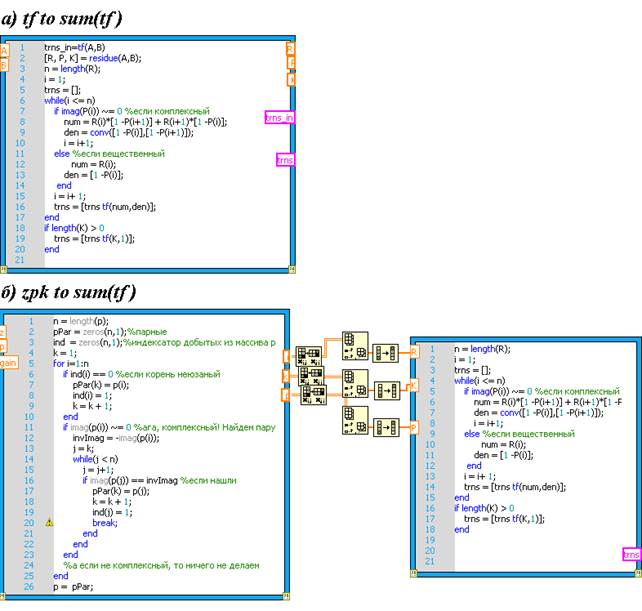
Рисунок 3. Алгоритмы перехода от одной передаточной функции к набору звеньев в узлах Mathscript Node
Преобразование исходной передаточной функции синтезированного фильтра (4) к виду (3) из форм представления в виде tf и zpk, полученных на этапе синтеза эллиптического фильтра (рисунок 1), дает практически идентичные результаты. Коэффициенты полученных передаточных функций различаются лишь в 14 знаке после запятой. Общий вид полученной суммы представлен ниже в выражении (5).
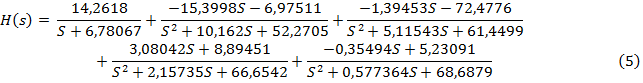
Для анализа параллельной декомпозиции цифрового фильтра (5) во временной и частотной области соберем модель в Simulation Module для вариантов синтеза в tf и в zpk, как показано на рисунке 4.

Рисунок 4. Фрагмент блок-диаграммы, реализующий параллельный фильтр в узле Simulation Loop для вариантов синтеза в tf и в zpk
На рисунке 5 приводятся погрешности параллельной модели эллиптического фильтра (5) во временной области для вариантов перехода к параллельным звеньям от единой передаточной функции высокого порядка (tf) и от представления в виде нулей и полюсов синтезированного фильтра (zpk). Погрешность вычисляется относительно исходной передаточной функции (4), моделируемой средствами инструментальной среды LabVIEW.
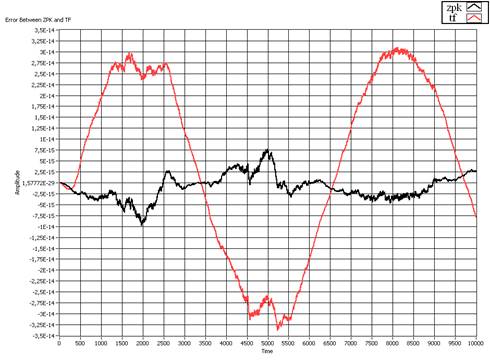
Рисунок 5. Сравнение погрешностей параллельной реализации фильтра относительно исходной передаточной функции для вариантов синтеза в tf и в zpk
На рисунке 5 можно увидеть, что погрешность при изначальном синтезе фильтра в форме zpk практически на порядок меньше погрешности передаточной функции фильтра, синтезированного в виде tf. Это объясняется неточностью нахождения корней полиномов нумератора и деноминатора при разбиении на сумму параллельных звеньев, в то время как форма zpk изначально представляет собой набор этих корней. Для цифровой реализации необходимо заменить непрерывные звенья первого и второго порядка на цифровые интегрирующие процессоры, основанные на численных методах интегрирования. Представляется целесообразным использовать численные методы, ориентированные на аппаратную реализацию, в т. ч. пригодные для распараллеливания вычислительного процесса. Такими свойствами, например, обладает метод, описанный в работе [1].
Заключение
Несмотря на выявленные недостатки, можно заключить, что предлагаемое разбиение цифровых фильтров, синтезированных как в форме zpk, так и в форме tf, на сумму интегрирующих звеньев первого и второго порядка имеет высокую степень эквивалентности относительно исходной передаточной функции, достаточную для современных задач цифровой обработки сигналов. В качестве аппаратной платформы для реализации полученных компьютерных моделей цифровых устройств рекомендуется использовать оборудование с вычислителями на базе ПЛИС, поскольку данный класс устройств обладает естественным параллелизмом, что позволяет увеличивать порядок фильтра для достижения необходимой точности, не уменьшая при этом скорость обработки сигнала.
Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации (Договор № 14.B37.21.0589).
Рецензенты:
Анисимов В. И., д.т.н., профессор кафедры систем автоматизированного проектирования, Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В. И. Ульянова (Ленина)», г.Санкт-Петербург.
Сольницев Р. И., д.т.н., профессор кафедры систем автоматизированного проектирования, Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В. И. Ульянова (Ленина)», г.Санкт-Петербург.



