Введение
Использование высокопрочных и высокомодульных волокон позволяет создавать композиционные материалы, обладающие малой массой, управлять физико-механическими, электрическими, теплофизическими свойствами, регулировать анизотропию этих характеристик, обеспечивая достижение максимальных характеристик в выбранном направлении. Указанные возможности позволяют применять такие материалы для создания конструкций с высокой весовой эффективностью для различных областей применения.
Назначение материала, требования, регламентирующие условия его работы в изделиях, определяют выбор схемы армирования, материала матрицы и армирующего наполнителя. Необходимость обеспечить высокую пластическую деформацию композиционного материала делает целесообразным применение в качестве материала матрицы термопластичных полимеров, способных переходить в высокоэластичное состояние и не претерпевающих химических превращений в процессе нагрева и охлаждения [3-5].
В настоящей работе решалась задача численного моделирования последствий механических воздействий на указанные полимерные нанокомпозиты, содержащие асимметричные включения.
Методика численного моделирования
В работе проводился расчет огрубленной (coarse-grained) мезоскопической модели. Моделировалась полиэтиленовая матрица, состоящая из 10 молекул полиэтилена из 5000 мономеров CH2. В coarse-grained модели полимер состоял из суператомов, которые представляют мономеры CH2.
Для молекулярно-динамического расчета использовалась комбинация гармонического потенциала, потенциала валентного угла и потенциала Леннарда-Джонса благодаря своей простоте и универсальности. Полная энергия полимера состоит из следующих частей [1].
1. Гармонический потенциал между соседними суператомами, соединенными химической связью:
![]()
kr = 700 ккал/моль, r0 = 1.557 Å.
2. Потенциал, зависящий от изменения валентного узла между соседними суператомами:
![]()
kθ = 112 ккал/моль, θ0 = 112 град
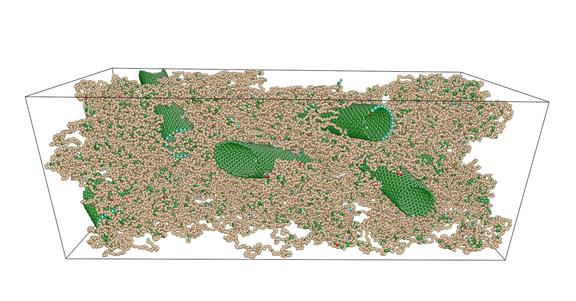

Рисунок 1. Пример огрубленной модели с углеродными нанотрубками.
3. Потенциал Леннарда-Джонса для описания Ван-дер-Ваальсовского взаимодействия между атомами, не связанными химической связью:
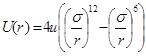
u = 0.113266 ккал/моль, σ = 4.28 Å.
Для ускорения генерации полиэтиленовой матрицы при плотности ~1 г/см3 сначала создавалась матрица плотностью 0.074375 г/см3, и в молекулярно-динамическом расчете производилось 3-осное сжатие до плотности 0.97 г/см3 при 500 K. Затем в течение 0.3 пс температура понижалась до 250 К для получения стеклообразного состояния полиэтилена.
Примеры начальных структур показаны на рисунках 1 и 2.


Рисунок 2. Пример огрубленной модели с углеродными нанотрубками (молекулы полимера не показаны)
Деформирование образца моделировалось путем одноосного растяжения с различными скоростями (показано на рисунке 3). Напряжение дано в относительных единицах. Для используемой модели CG-потенциала 106 отн. ед. = 20 МПа. Черная и красная линия соответствуют скоростям растяжения, отличающимся на порядок величины.
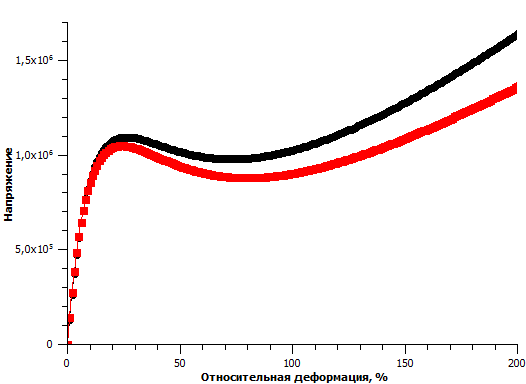
Рисунок 3. Зависимость напряжения в образце от величины относительной деформации
Результаты показывают наличие слабой зависимости напряжения в образце от скорости растяжения. Однако ее влияние не превышает требуемого уровня точности для расчета (как в данном примере) предела текучести нанокомпозитного материала (10%).
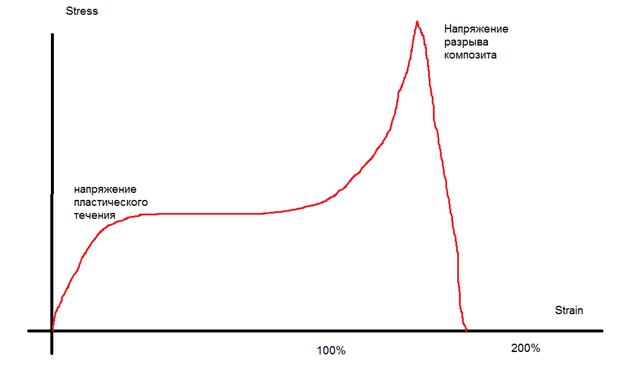
Рисунок 4. Качественный пример выходных данных
Рассчитанные значения напряжения и модуля упругости при одноосном растяжении аморфного полиэтилена Сравнение полученных с помощью МД-моделирования данных с экспериментальными приведено в таблице 1.
Таблица 1 - Значения напряжения и модуля упругости для UHMWPE
|
|
МД |
Эксперимент |
|
Напряжение при 1% растяжения, МПа |
48.6 |
37.1±1.8 |
|
Модуль упругости, ГПа |
4.8 |
3.7±0.17 |
Расхождение данных молекулярно-динамического моделирования с экспериментальными можно объяснить, в частности, значительной разницей молекулярных масс и числа мономеров в полиэтилене.
Функциональных форм для подобного эмпирического описания потенциалов предложено большое количество. Например, в [2] используется потенциал, представленный следующими компонентами:
![]()
b = 13.74302 эВ/Å2, l0 = 1.53 Å,
![]()
θ0 = 109.47 град, α1 = 5.2038893˟10-4 эВ/град2, α2 = 4.9955775˟10-6 эВ/град3,
![]()
![]()
![]() ,
,
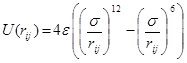
![]()
где r0, l0 – равновесные длины связи, θ0 – равновесное значение угла между соседними атомами в молекуле.
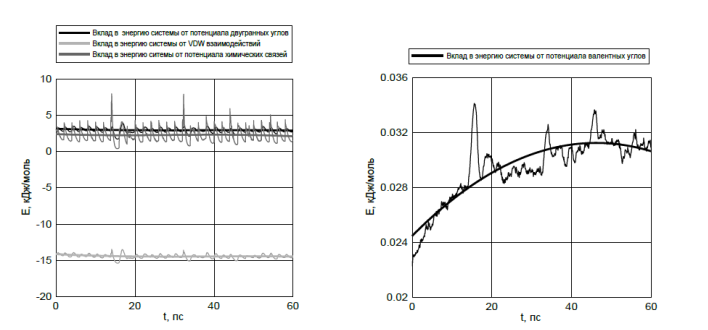
Рисунок 5. Вклады в суммарную потенциальную энергию молекулярной системы
Анализ энергетических параметров молекулярной системы (рис. 5) свидетельствует о том, что основным механизмом механического поведения нанокомпозита при одноосном растяжении является деформация валентных углов; энергии химических связей, парных и торсионных взаимодействий остаются практически неизменными.
Выводы
В данной работе методом молекулярно-динамического моделирования исследована структура и физико-механические свойства полиэтилена. Для определения эффективных упругих характеристик моделировалось различные типы деформирования образца: одноосное растяжение и нагружение образца внешним давлением.
Результаты показывают наличие слабой зависимости напряжения в образце от скорости растяжения. Также показано, что основным механизмом механического поведения нанокомпозита при одноосном растяжении является деформация валентных углов.
Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации в рамках федеральной целевой программы «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007-2013 годы», государственный контракт 01 марта 2013 г. № 14.514.11.4053.
Рецензенты:
Кривоножко В.Е. д.ф.-м.н., заведующий кафедрой АСУ НИТУ «МИСиС», г. Москва.
Красильников О.М., д.ф.-м.н., профессор НИТУ «МИСиС», г. Москва.



