Введение
Современный подход к созданию распределенных программно-информационных технологий для корпоративных и производственных структур основан на концепции гетерогенных систем, состоящей в объединении в единую систему или сеть множества разнородных обрабатывающих средств (процессоров), средств хранения, обработки информации и средств управления (разноплатформенные СУБД, различные учетные системы и т. д.). При этом возникает необходимость сформировать необходимый набор инструментов и политик, который позволил бы минимизировать ключевые риски используемых гетерогенных систем на всех стадиях и фазах жизненного цикла, в частности, при планировании задач обработки информации. При этом необходимо учитывать, что в распределенных системах режим реального времени предполагает лимитирование времени ответа системы управления на запрос объекта. Ограничение на время реакции связывается в этом случае с выполнением периодических действий [5, 6].
Таким образом, при реализации периодичных задач формирование алгоритмов распределенной обработки информации и управления должно осуществляться с учетом ограничений, представленных в форме классов ресурсов, жесткого регламента задач и временных пределов реализации задач.
Методы и материал исследования
Рассмотрим существующие ограничения на классы ресурсов. Решения, предложенные ранее в [1,3,4], были связаны, прежде всего, с распределением процессоров. Вычислительные ограничения выражались в терминах времени выполнения и отношений предшествования.
Предлагаемая модель расширяет понятие стандартной модели, состоящей из множества r задач неравной длительности, связанных отношением предшествования и выполняемых на неприоритетной основе набором из n идентичных процессоров. В [6] отмечается, что проблема планирования зависимых задач очень сложна, нахождение ее оптимального решения требует больших вычислительных ресурсов, сравнимых с теми, которые требуются для собственно выполнения задач управления. Отметим, что при подходе, рассматриваемом в [6], планирование приближается к статическому варианту.
В нашем случае дополнительно предполагается наличие множества ресурсов R = {R1, …, RS}. Если задаче Tj необходим ресурс Ri, то это требование принимается во внимание в течение всего периода выполнения задачи. Потребность задачи Tj в ресурсе Ri обозначается через pij (0 ≤ pij ≤ 1).
Пусть ri(t) обозначает общее количество ресурсов Ri, которое используется в момент времени t. Тогда ri(t) = Sum(pij) для всех Tj, выполняемых в момент времени t. Основная проблема заключается в обосновании критерия, отражающего степень влияния различных списков планов для этой модели на время завершения задачи (w).
Предположим, что для двух произвольных списков L и L’ расширенная система из n процессоров выполняет набор из r задач с результирующими временами завершения w и w’ соответственно. Для такой среды предлагается ряд решений, которые дают следующие результаты:
1) R = {R1} (в системе существует только один вид ресурсов, отличных от процессора) – w / w’ ≤ n;
2) R = {R1} и независимости всех задач - w / w’ ≤ (3 – 1 / n);
3) R = (R1, R2, …, RS}, независимости задач и n ≥ r - w / w’ ≤ S + 1.
В ходе исследования предложенной модели в гетерогенных системах были получены ограничения на количество задач, число процессоров и правила формирования списка используемых статических планов. Также было показано, что предложенные алгоритмы снижают эффективность, когда устраняются ограничения на ресурсы.
Классическим примером планирования независимых задач для жестких систем реального времени с одним процессором является алгоритм, разработанный Лью и Лейландом [9]. Этот алгоритм является динамическим, он использует вытесняющую многозадачность и основан на относительных статических (неизменяемых в течение жизни задачи) приоритетах. Целью является минимизация числа процессоров, требуемых для выполнения ряда задач при временных ограничениях на начало / конец выполнения заданий.
Пусть Ei – максимальное время выполнения одной итерации задачи Ji, а fi – частота выполнения. Таким образом, каждой задаче Ji соответствуют два параметра Ji: (fi, Ei), 1 ≤ i ≤ n, где n – количество включаемых в план задач.
Период повторения равен Ti, величине обратной fi. Если n задач с J1 по Jn распределены так, что fi > fi + 1, то предполагается, что fi = 2fi + 1. При этом к реализации допускаются задачи с любой частотой.
Рассматривая ограничения на время реакции системы, проанализируем периодичные задачи первого класса (с бинарным частотным распределением). Множество задач, удовлетворяющих бинарному частотному распределению, приведено в табл. 1. На рис. 1 показаны задачи J1 и J2, спланированные на разных процессорах. На рис. 2 показан план, уменьшающий количество процессоров с двух до одного. Проблемой является определение минимального количества процессоров без перебора всех возможных альтернатив.
Таблица 1
Характеристики для множества задач с бинарным частотным распределением
|
Задача |
Частота |
Период |
Время выполнения |
|
J1 |
1/4 |
4 |
1 |
|
J2 |
1/8 |
8 |
2 |
|
J3 |
1/16 |
16 |
1½ |
|
J4 |
1/32 |
32 |
5 |
|
J5 |
1/64 |
64 |
3 |
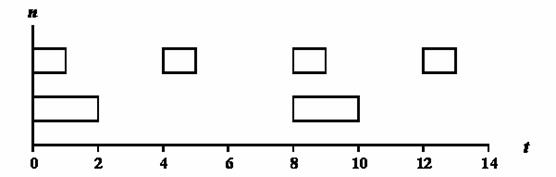
Рис. 1. Временная диаграмма для первых двух задач из табл. 1
Заметим, что слияние двух задач, приведенное на рис. 2, создает новую периодичную задачу с периодом t1 (равным 2T1) и временем выполнения е1 (равным T1 + E1). Кроме того, имеются два промежутка с простоями: I1 – периодичный простой с длительностью t1 – е1 и ![]() – принудительное время простоя длинной I1 – E2 (обозначение
– принудительное время простоя длинной I1 – E2 (обозначение ![]() указывает, что принудительное время простоя получается, когда Jj объединяется с Ji).
указывает, что принудительное время простоя получается, когда Jj объединяется с Ji).
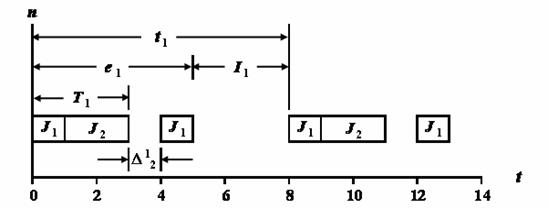
Рис. 2. Ослабление ограничений на число процессоров путем слияния задач
В процессе объединения остальных задач плана нет необходимости рассматривать размещение задач в интервале принудительного простоя. Вместо этого для такой среды план с минимальным числом процессоров формируется в соответствии со следующим алгоритмом:
1) Пусть J1*, J2*, … – подмножества задач, назначаемых процессорам P1, P2,… Сначала J1* = J2* = … = Æ, а I1 = I2 = … = ∞. Всякий раз, когда задача Jj добавляется в некоторое пустое подмножество Jl*, Il = Tj – Ej.
2) Чтобы назначить очередную задачу Ji, необходимо найти наименьшее Ii такое, чтобы выполнялось условие Ei ≤ Ii. Добавить Ji в подмножество Jl*.
Оптимальный план для набора задач из табл. 1 показан на рис. 3. Этот результат может быть обобщен и для случая, когда fi = k fi + 1, k – положительное целое число больше единицы.

Рис. 3. Оптимальный план для задач из табл. 1.
В случае, когда устранена бинарная частотная связь между задачами, принятая ранее, т. е. в режиме реального времени реализуются периодичные задачи с независимым распределением частот, то задача становится более сложной, а оптимальное решение не может быть найдено точными методами. Были разработаны эвристические алгоритмы и проведено их относительное сравнение с применением моделирования. Предлагаемые подходы делятся на три группы.
1. В порядке уменьшения частоты. Задачи располагаются в порядке уменьшения частоты, и их назначение также должно проходить в этом порядке.
2. В порядке уменьшения критерия загрузки. Критерий загрузки задачи Ji, обозначаемый Li, определяется следующим образом: Li = Ei / Ti.
3. Сохранение минимальной длины критического интервала. Критический интервал между двумя задачами определяется как минимальный интервал между временем завершения первой задачи и временем начала выполнения второй задачи в некоторой точке плана. Определение этого интервала не включает первую итерацию обоих задач, где по определению начало выполнения второй задачи немедленно следует за завершением первой задачи.
При тестировании данных методов, задачи разделялись на два класса. В 1-м классе частоты задач кратны более чем двум базовым частотам, а во 2-м – не более чем двум базовым частотам. Ни один из алгоритмов не показал значительного превосходства над другими. Однако подход 2 исключительно хорошо показал себя на задачах первого класса. Подход 3 лучше решает некоторые задачи второго класса, а оба подхода 1 и 2 неплохо решают задачи, которые оказались трудными для подхода 3. Во многих случаях уменьшение частот задач или времен их выполнения может привести к увеличению количества требуемых процессоров. И наоборот, требуемое количество процессоров может быть уменьшено за счет увеличения частот задач или времен выполнения, т. е. путем увеличения загруженности процессора.
В контексте решения задач обработки данных в гетерогенных распределенных системах (ИС) одной из проблем является обоснование критериев формирования планов обработки. Например, решение разграничить планы обработки данных по критерию количества процессоров для обработки графа задачи не является очевидным ввиду большого количества других факторов, которые могут использоваться при классификации задач обработки. Так, в ходе наших исследований были определены следующие факторы планов обработки данных в гетерогенных системах: количество процессоров; продолжительность задачи; структура графа предшествования; прерывание задач; периодичность выполнения конвейерного плана обработки данных; наличие и отсутствие пределов; планирование с ограниченными ресурсами; гомогенные и гетерогенные процессоры; показатели эффективности (время окончания или завершения; количество используемых процессоров; среднее время реализации конвейерного плана обработки задач; загрузка процессора; время простоя процессора), эффективность алгоритмов в целом.
Результаты
Разработанное модельно-алгоритмическое обеспечение планирования задач обработки данных для класса конвейерных планов (в которых существует последовательная взаимосвязь между несколькими процессорами, включенными в совместное выполнение ряда задач) реализует алгоритм Джонсона (JO) для формирования двухмашинных конвейерных планов обработки данных. В данном алгоритме реализована процедура сравнительного анализа конвейерных планов с начальной очередностью и с минимальным временем потока (так называемый SPT-план), что отображено на рис. 4.
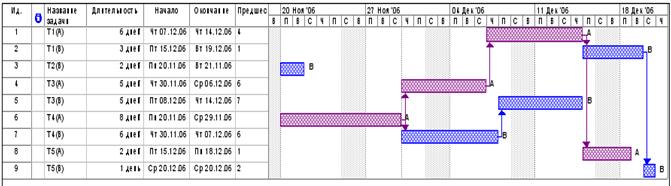
Рис. 4. Двухмашинный конвейерный план с минимальным временем потока
Следует отметить, что конвейерные планы рассматриваются не в качестве разновидности многопроцессорного планирования, так как задача, которую необходимо в этом случае выполнить, должна быть обслужена одним из процессоров, а потом другими. Это чередование должно соблюдаться для всех задач, входящих в план, но требования идентичности процессоров нами не вводится.
Алгоритм Джонсона упорядочивает задачи, одновременно доступные на двухмашинном конвейерном плане, таким образом, чтобы минимизировать максимальное время потока. По алгоритму Джонсона задача Ti предшествует Tj, если ![]() и
и ![]() , где Ai и Bi представляют требования Ti для процессора класса А и класса В соответственно. Процедуры предыдущего алгоритма обобщены для ситуации, когда более чем один процессор может существовать в каждом из двух классов – классе А и классе В. Для модифицированного алгоритма Джонсона (MJO) в конвейерной среде с m процессорами класса А и n процессорами класса В задача Ti предшествует Tj, в соответствии с (MJO), если
, где Ai и Bi представляют требования Ti для процессора класса А и класса В соответственно. Процедуры предыдущего алгоритма обобщены для ситуации, когда более чем один процессор может существовать в каждом из двух классов – классе А и классе В. Для модифицированного алгоритма Джонсона (MJO) в конвейерной среде с m процессорами класса А и n процессорами класса В задача Ti предшествует Tj, в соответствии с (MJO), если ![]() .
.
Эта модификация, фактически ослабляет действие нескольких ограничений, используемых в общем алгоритме Джонсона. Во-первых, допускается наличие более двух машин, а во-вторых, предполагается, что объем доступной промежуточной памяти равен нулю. Поэтому также предлагается процедура сравнительного анализа трехмашинных конвейерных планов: FSIIS-план с бесконечной промежуточной памятью, FSNIS-план без промежуточной памяти, FSFIS-план, с ограниченной промежуточной памятью.
Иллюстрация программной реализации трехмашинного конвейерного FSNIS-плана без промежуточной памяти приведена на рис. 5.
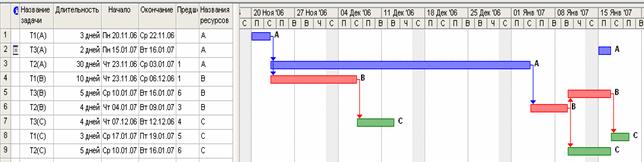
Рис. 5. Трехмашинный конвейерный FSNIS-план без промежуточной памяти
Заключение
Предложенный подход решения задач обработки данных в гетерогенных распределенных системах дает следующие преимущества: увеличение пропускной способности ИС конвейерного типа; обеспечение однородности функций конвейерной ИС, что позволяет уменьшить требования к ИС; сокращение времени и повышение эффективности коммуникаций между процессорами; возможность мониторинга загруженности ИС конвейерного типа в режиме реального времени. Чтобы пользователю не пришлось производить мониторинг всех конвейерных планов, вводятся пороговые допустимые значения текущих задач, и контрольные устройства системы будут извещать о превышении порога.
Таким образом, технология, базирующаяся на конвейерной обработке данных, предоставляет возможности формирования показателей эффективности работы отдельных процессоров, реализующих конвейерные планы для неоднородных систем. При этом значительно повышается эффективность процессов обработки информации за счет обоснования факторов планирования задач обработки данных в информационных системах.
Рецензенты:
Лаптенок В.Д., д.т.н., профессор кафедры информационно-управляющих систем ФГБОУ ВПО «Сибирский государственный аэрокосмический университет им. академика М. Ф. Решетнева», г. Красноярск.
Лапко В.А., д.т.н., профессор кафедры космических средств и технологий ФГБОУ ВПО «Сибирский государственный аэрокосмический университет им. академика М. Ф. Решетнева», г. Красноярск.



